PAT-1003 Emergency（Dijkstra）

1003 Emergency （25 分)

As an emergency rescue team leader of a city, you are given a special map of your country. The map shows several scattered cities connected by some roads. Amount of rescue teams in each city and the length of each road between any pair of cities are marked on the map. When there is an emergency call to you from some other city, your job is to lead your men to the place as quickly as possible, and at the mean time, call up as many hands on the way as possible.

Input Specification:

Each input file contains one test case. For each test case, the first line contains 4 positive integers: N (≤500) - the number of cities (and the cities are numbered from 0 to N−1), M - the number of roads, C₁ and C₁- the cities that you are currently in and that you must save, respectively. The next line contains N integers, where the i-th integer is the number of rescue teams in the i-th city. Then M lines follow, each describes a road with three integers c₁ , c₁ and L, which are the pair of cities connected by a road and the length of that road, respectively. It is guaranteed that there exists at least one path from C₁ to C₁.

Output Specification:

For each test case, print in one line two numbers: the number of different shortest paths between C₁ and C₁ , and the maximum amount of rescue teams you can possibly gather. All the numbers in a line must be separated by exactly one space, and there is no extra space allowed at the end of a line.

Sample Input:

5 6 0 2

1 2 1 5 3

0 1 1

0 2 2

0 3 1

1 2 1

2 4 1

3 4 1

Sample Output:

2 4

算法说明：

算法的大体意识是求出发城市到到目的城市的单元最短路径，并记录单元最短路径的条数并输出，在这些最短路径中再求得能聚集医疗队的最大数并输出。

第一行输入分别为：城市的个数n，路径的个数m，出发城市，目的城市

第二行输入为：各个城市医疗队的数量

最后m行每行为：c₁ 到c₁以及权重

求单元最短路径首先应该想到的是Dijkstra算法，单元最短路径不止一条，并且要记录出发城市到目的城市的医疗队数量，可以采用vector进行存储，每个节点的长度代表单元路径条数，值代表医疗队数量。

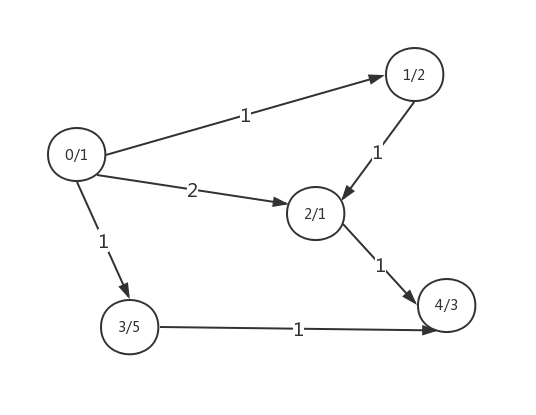
**城市医疗队分布图**
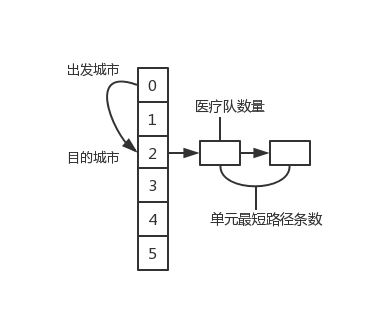
**vector存储结构**
```c++
// 1003_Emergency.cpp : Defines the entry point for the console application.
//

include "stdafx.h"

include

include <string.h>

include

define MaxSize 500

using namespace std;

int Graph[MaxSize][MaxSize]; // 图数组

int vis[MaxSize]={0},dis[MaxSize];

int curNum[MaxSize]={0};

int n,m,cur,des; // n 城市个数，m 为路径，cur 为目前所在城市，des 为目标城市

const int INF=0x7f;

vector vec[MaxSize];

// 输入数据

void Input(){

int i,x,y,z;

cin>>n>>m>>cur>>des;

memset(Graph,-1,sizeof(Graph));

for(i=0;i<n;i++)

dis[i]=MaxSize;

// 每个城市的救援队数量

for(i=0;i<n;i++)

cin>>curNum[i];

// 输入图

for(i=0;i<m;i++){

cin>>x>>y>>z;

Graph[x][y]=z;

Graph[y][x]=z;

}

}

void push(int target,int dataid)

{

for(int i=0;i<vec[dataid].size();i++)

// 当前城市医疗队数量+前一节点医疗队数量

vec[target].push_back(vec[dataid][i]+curNum[target]);

}

void Dijkstra(int cur,int des){

int i,Min;

int cen=cur;

vis[cur]=1; // 已访问

vec[cur].push_back(curNum[cur]);

dis[cur]=0;

while(true){

// 找到相邻节点 更新距离

for(i=0;i<n;i++){

if(vis[i]0&&Graph[cen][i]!=-1){

if(Graph[cen][i]+dis[cen]<dis[i]){

dis[i]=Graph[cen][i]+dis[cen];

vec[i].clear(); // 清除当前城市数据节点

push(i,cen);

}else if(Graph[cen][i]+dis[cen]dis[i]){

push(i,cen);

}

}

}

// 找到下一节点

Min=INF;

for(i=0;i<n;i++){

if(vis[i]0&&dis[i]<Min){

Min=dis[i];

cen=i;

}

}

vis[cen]=1;

if(cendes)

break;

}

}

int main(int argc, char* argv[])

{

Input();

Dijkstra(cur,des);

vector desVec=vec[des];

cout<<desVec.size()<<' ';

// 找单元最短路径最大医疗队数量

int MaxValue=desVec[0];

for(int i=1;i<desVec.size();i++){

if(MaxValue<desVec[i]){

MaxValue=desVec[i];

}

}

cout<<MaxValue << endl;

return 0;

}

**<center>2020考研打卡第一天，你可知道星辰之变，骄阳岂是终点？千万不要小看一个人的决心。加油！！！</center>**
**<center>人生为棋，我愿为卒，行动虽慢，可谁也没见我后退一步。</center>**