Luogu 3421 [POI2005]SKO-Knights - Exgcd

Description

给出一个骑士的 $N$种 中行走的方式 $(a_i, b_i)$， 可以使骑士的坐标$(-a,-b)$或$(+a,+b)$。

我们需要找出 第二个骑士的 两种行走方式 $(c_1, d_1)$ 和 $(c_2, d_2)$ 使得 两个骑士能走到的点 完全相同。

保证$a_i, b_i$ 不会同时$=0$。

Solution

真的是比较神奇的解法， 只需要会exgcd就能够做的题（然而我真的没有想到。

我们要将  两个 不竖直的 向量 $(a_1, b_1)$ ， $(a_2, b_2)$ 转换成 等价的  一个不竖直向量$(a_3,b_3)$和 一个竖直向量$(0,b_4)$

也就是下图中的 两条绿线

　　　（我是真的不会画图QAQ）　图源

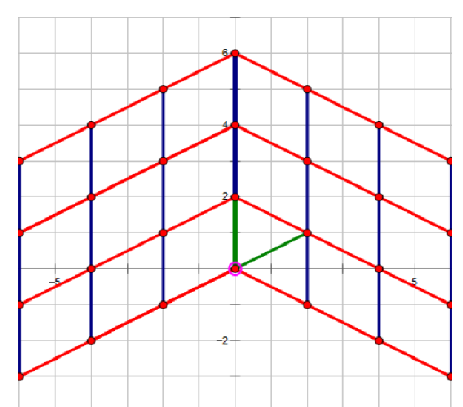
然后我们就能发现  能走到的点  的 水平距离 为 $gcd(a_1, a_2)$。

并且 横坐标相同的点 ， 纵坐标的差 为 $(a_1 \times b_2 \ - \ a_2 \ times b_1)\div gcd(a_1,a_2)$

　　证明： 设 $a_1 \times x_1 + a_2 \times y_1= $横坐标

　　　　　那么 $b_1 \times x_1 + b_2 \times y_1=$纵坐标

　　　　　根据扩展欧几里得， $x = x_1  + k \times a_2 \div gcd, y  = y_1 - k \times a_1 \div gcd$，

　　　　　　　　　　　　　　把$x, y$带入第二个式子， 就得到了纵坐标差为 $(a_1 \times b_2 \ - \ a_2 \times b_1)\div gcd(a_1,a_2)$。

接着使 $a_3 = gcd(a_1,a_2)$,  并算出 满足  $a_1 \times x_1 + a_2 \times y_1= gcd(a_1,a_2)$ 的 $x_1$, 和$y_1$。

令$b_3 = b_1 \times x_1 + b_2 \times y_1$。

$b_4 = (a_1 \times b_2 \ - \ a_2 \times b_1)\div gcd(a_1,a_2)$

并且这两个向量是与 转换之前的向量 等价， 即它们所构成的 所有坐标都相同。

所有的竖直向量都可以合并成 $gcd$， 所以我们把得到的 竖直向量与之前的竖直向量合并成一个。

这样每一次操作 两个向量 都会变成 一个向量。 最后只剩一个竖直向量 和 一个不竖直向量 就是要的答案了。

Code

 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<queue>
 #define rd read()
 using namespace std;
 typedef pair<int, int> P;

 const int N = 1e5 + ;

 int n, ans1, ans2;

 queue<P> q;

 int read() {
     int X = , p = ; char c = getchar();
     for (; c > '' ||  c < ''; c = getchar())
         if (c == '-') p = -;
     for (; c >= '' && c <= ''; c = getchar())
         X = X *  + c - '';
     return X * p;
 }

 int gcd(int x, int y) {
     if (!x || !y)
         return x + y;
     return gcd(y, x % y);
 }

 int exgcd(int a, int b, int &x, int &y) {
     if (b == ) {
         x = ; y = ;
         return a;
     }
     int d = exgcd(b ,a % b, x , y), z = y;
     y = x - a/b * y; x = z;
     return d;
 }

 #define fir first
 #define sec second

 int main()
 {
     n = rd;
     for (int i = ; i <= n; ++i) {
         int a = rd, b = rd;
         if (a == )    ans2 = gcd(ans2, b);
         else q.push(P(a, b));
     }
     for (; q.size() > ;) {
         P u = q.front(), v; q.pop();
         v = q.front(); q.pop();
         int x, y;
         int a = exgcd(u.fir, v.fir, x ,y), b = u.sec * x + v.sec * y;
         int t = (u.fir * v.sec - u.sec * v.fir) / a;
         q.push(P(a, b));
         ans2 = gcd(ans2, t);
     }
     printf("0 %d\n", ans2);
     if (q.empty()) printf("0 %d\n", ans2 * );
     else {
         P t = q.front();
         printf("%d %d\n", t.fir, t.sec);
     }
 }