Konig定理

由匈牙利数学家柯尼希（D.Konig）于1913年首先陈述的定理。
定理的内容：在0-1矩阵中，1的最大独立集合最小覆盖包含的元素个数相同，等价地，二分图中的最大匹配数等于这个图中的最小点覆盖数。

证明:

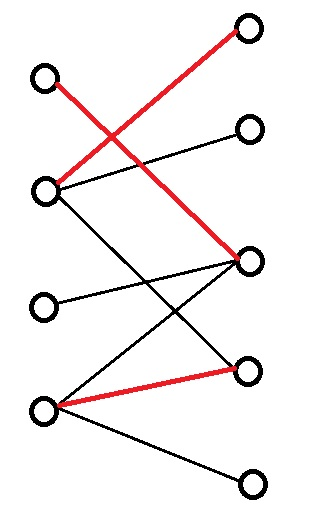
对于上面的二分图，它的最大匹配(不唯一)已经用红线标出来了，

然后我们对于右边或左边(这里按右边为例)没有匹配的点，我们从它出发走交替路(这里有介绍)，会经过若干节点
将所有从右边没有匹配的点开始的交替路上的所有的点标注起来(如下图标蓝的点)

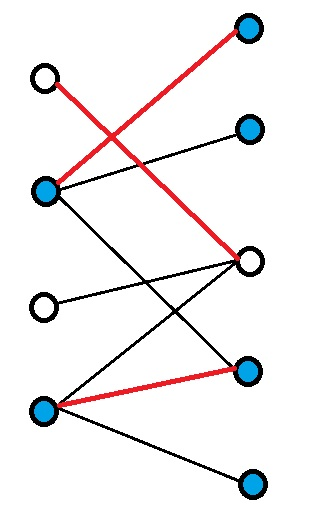
可以证明左边所有被标注的点都是被匹配的点(否则从未匹配的点到未匹配的点的交替路就是增广路)
右边所有没有被标注的点都是被匹配的点(或是没连任何边的点，可以忽略。否则可以从它开始走任意非匹配边，它就会被标注)
这些点就是最小覆盖点集(被标红)

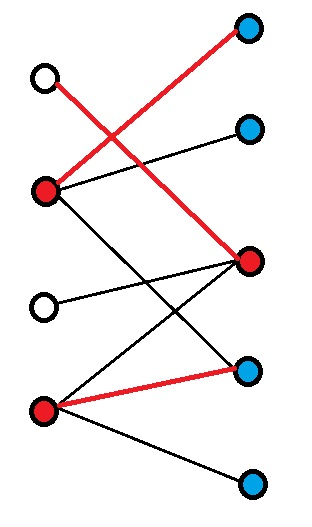
因为对于所有右边被标注的点连的边,其左边的点都被标注了，会被覆盖
假设左边的点是不是匹配点且没被标注，则当前边一定不是匹配边，可以加入交替路中，所以假设不成立
假设左边的点是匹配点且没被标注，则当前边一定是匹配边且不在交替路中，那么右边的这个点也是匹配点且被标记，那么右边的这个点已经连了一个在交替路中的匹配边，但一个点最多会有一个匹配边，所以假设不成立

对于所有左边没被标注的点连的边，其右边的点都没被标注
假设右边的点是匹配点且被标注，则当前边一定不是匹配边，可以加入交替路中，所以假设不成立
假设右边的点不是匹配点且被标注，则当前边一定不是匹配边，可以加入交替路中，所以假设不成立

所以所有边都被覆盖了

Konig定理及证明的更多相关文章

  1. 二分图最小覆盖的Konig定理及其证明,最小的覆盖证明

    [转http://www.cppblog.com/abilitytao/archive/2009/09/02/95147.html  ->  http://yejingx.ycool.com/p ...

  2. 【Learning】最小点覆盖（二分图匹配） 与Konig定理证明

    (附一道例题) Time Limit: 1000 ms   Memory Limit: 128 MB Description 最小点覆盖是指在二分图中,用最小的点集覆盖所有的边.当然,一个二分图的最小 ...

  3. 二分图最大匹配的König定理及其证明

     二分图最大匹配的K?nig定理及其证明 本文将是这一系列里最短的一篇,因为我只打算把K?nig定理证了,其它的废话一概没有.    以下五个问题我可能会在以后的文章里说,如果你现在很想知道的话,网上 ...

  4. Computer Science Theory for the Information Age-6: 学习理论——VC定理的证明

    VC定理的证明 本文讨论VC理论的证明,其主要内容就是证明VC理论的两个定理,所以内容非常的枯燥,但对于充实一下自己的理论知识也是有帮助的.另外,VC理论属于比较难也比较抽象的知识,所以我总结的这些证 ...

  5. 《University Calculus》-chaper8-无穷序列和无穷级数-泰勒定理的证明

    泰勒定理: 证明:

  6. latex中使用定理、证明、缩进

    1.定理和证明 \documentclass[a4paper,UTF8]{article} \usepackage{ctex} \usepackage{amsthm,amsmath,amsfonts, ...

  7. xdoj-1057(Lucas定理的证明及其模板）

    Lucas定理的证明: 转自百度百科(感觉写的还不错) 首先你需要这个算式:    ,其中f > 0&& f < p,然后 (1 + x) nΞ(1 + x) sp+q Ξ ...

  8. hdu5391-Zball in Tina Town-威尔逊定理(假证明)

    Tina Town is a friendly place. People there care about each other. Tina has a ball called zball. Zba ...

  9. 初等数论-Base-2(扩展欧几里得算法，同余，线性同余方程，(附：裴蜀定理的证明))

    我们接着上面的欧几里得算法说 扩展欧几里得算法 扩展欧几里德算法是用来在已知a, b求解一组x,y,使它们满足贝祖等式\(^①\): ax+by = gcd(a, b) =d(解一定存在,根据数论中的 ...

随机推荐

  1. JS去重算法

    1.遍历数组法 它是最简单的数组去重方法(indexOf方法) 实现思路:新建一个数组,遍历去要重的数组,当值不在新数组的时候(indexOf为-1)就加入该新数组中: var arr=[2,8,5, ...

  2. openwrt xfrp移植

    对开源软件表示支持 https://github.com/KunTengRom/xfrp 上传编译,选择 cp .config xxx make 刷机 客户端配置文件: /tmp/etc# cat x ...

  3. thinkphp 多层mvc

    hinkPHP基于MVC(Model-View-Controller,模型-视图-控制器)模式,并且均支持多层(multi-Layer)设计. 模型(Model)层 默认的模型层由Model类构成,但 ...

  4. window.location 对象中各种方法的用途

    一.简介 属性 描述 hash 从井号 (#) 开始的 URL(锚) host 主机名和当前 URL 的端口号 hostname 当前 URL 的主机名 href 完整的 URL pathname 当 ...

  5. ThinkPHP 的缓存大概多久更新一次

    ThinkPHP 的缓存大概多久更新一次可以自己设置: thinkPHP的缓存默认是文件缓存,保存在Runtime文件夹里面, 如果不设置过期时间,且不清除Runtime文件,就会一直存在. 如果设置 ...

  6. Jenkins 自动部署

      一.安装插件[系统管理 → 插件管理 ] 为了通过SSH上传war包,我们需要安装Publish Over SSH 插件. 二.添加SSH 服务器[系统管理→系统设置] 参数说明: Name:ss ...

  7. 同步+TASK异步请求

    using System; using System.Collections.Generic; using System.ComponentModel; using System.Data; usin ...

  8. neo4j算法（1）-介绍

    neo4j为图数据库,其中涉及的也就为图算法,图算法被用来度量图形,节点及关系. 在neo4j中,通过call algo.list() 可查看neo4j中的算法列表. 在neo4j官方文档中,主要记录 ...

  9. typeerror: __init__() missing 2 required positional arguments: 'inputs' and 'outputs'

    1 问题描述 使用下边这条命令去检查 TensorFlow Object Detection API是否正确安装: python object_detection\builders\model_bui ...

  10. 9个永恒的UI设计原则

    很多人都在寻找那些能够帮助他们快速提升设计能力的方法,但你是否想过,自己身上的哪些方面会对你的设计产生影响呢?是使用工具的技巧,对设计的理解和态度,还是你的生活习惯呢?我想说所有这些都是决定你的设计是 ...