电信NBIOT平台的CA证书上传-消息订阅回调地址检测503错误

在NBIOT北向开发过程中，遇到消息订阅回调地址检测503错误，经过论坛查询与文档查阅一直都没有解决问题，大多人都说是RESTful地址格式问题，但其实不是。最终发现是我们在电信平台创建应用时，上传CA证书中.pem证书问题。我是在阿里云申请的免费证书，IIS环境，将证书下载下来后，如果直接将PEM格式文件上传到电信平台，那么消息订阅回调地址检测503错误，那为什么CA证书不正确，因为我们上传CA证书只包含了一级CERTIFICATE！！而实际上是有多级，如下图（CHROME浏览器）：

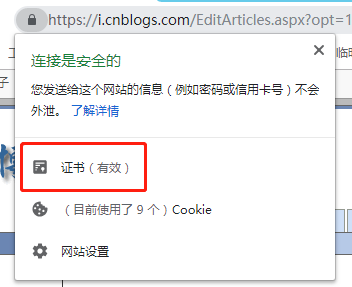
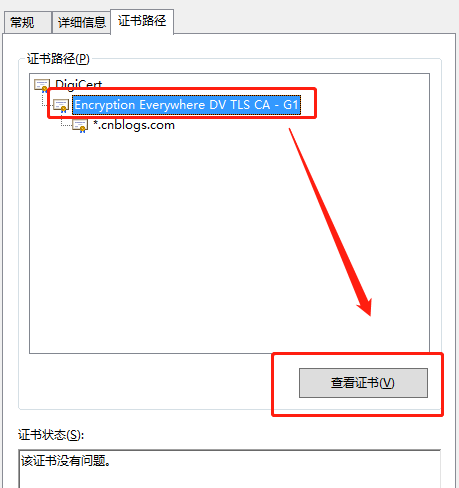
在证书路径下可以看到有三级证书：

那么我们需要导出其它二级证书信息，如图：

证书导出向导一定要选择BASE64

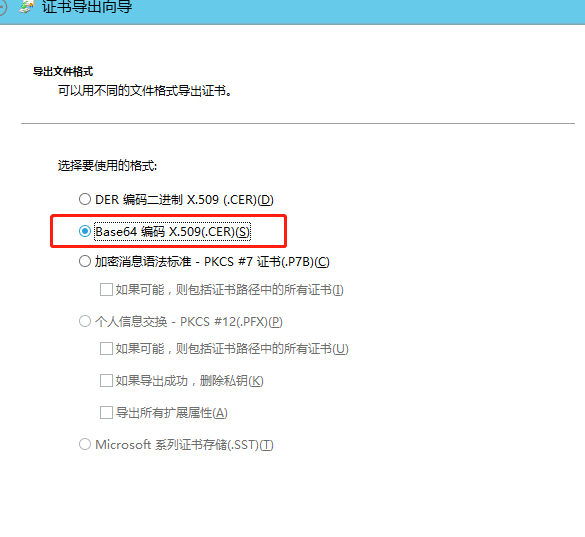
然后下一步，保存好cer文件，重复以上步骤，一级一级导出，如图：

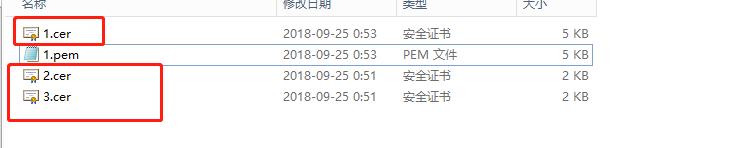
导出完毕后，.cer文件用记事本打开，将里面内容依次复制粘贴到.pem文件中，如下图：

完成后，再将.pem上传到电信nb lot平台CA证书中，更新服务器上原来pem文件即可。

再登录电信NBIOT平台进行检测，我们可以看到通过检测：