ACWing 238 银河英雄传说

最近带权并查集这块比较薄弱，直接看食物链看不懂，就老实一步步来了。

---

有一个划分为N列的星际战场，各列依次编号为1,2,…,N。

有N艘战舰，也依次编号为1,2,…,N,其中第i号战舰处于第i列。

有T条指令，每条指令格式为以下两种之一：

1、M i j，表示让第i号战舰所在列的全部战舰保持原有顺序，接在第j号战舰所在列的尾部。

2、C i j，表示询问第i号战舰与第j号战舰当前是否处于同一列中，如果在同一列中，它们之间间隔了多少艘战舰。

现在需要你编写一个程序，处理一系列的指令。

输入格式

第一行包含整数T，表示共有T条指令。

接下来T行，每行一个指令，指令有两种形式：M i j或C i j。

其中M和C为大写字母表示指令类型，i和j为整数，表示指令涉及的战舰编号。

输出格式

你的程序应当依次对输入的每一条指令进行分析和处理：

如果是M i j形式，则表示舰队排列发生了变化，你的程序要注意到这一点，但是不要输出任何信息；

如果是C i j形式，你的程序要输出一行，仅包含一个整数，表示在同一列上，第i号战舰与第j号战舰之间布置的战舰数目，如果第i号战舰与第j号战舰当前不在同一列上，则输出-1。

数据范围

N≤30000,T≤500000

原题链接:https://www.acwing.com/problem/content/240/

---

由于直接维护每对战舰之间的距离的时间复杂度非常大，所以我们考虑维护每个战舰到队头的距离，这样如果两只战舰在同一列上且i != j，那么我们就直接通过两个战舰各自到队头的距离相减得到答案，所以我们的查询函数可以这么写：

int Query(int a, int b)
{
    if(a == b) return ;
    if(issame(a, b)) return abs(d[a] - d[b]) - ;

    return -;
}

既然查询总是涉及子节点跟祖宗节点产生直接联系，那么我们可以考虑使用带权并查集来维护这个d[i]，这个d[i]代表自己到父节点的距离，但是由于并查集的路径压缩，最终每个子节点的父节点都会变成他们的祖宗，也就是说这个d[i]就变成了子节点到祖宗的距离。

我们知道，对于祖宗来说，它到自己的距离是0，所以祖宗的d[i]是0，同时我们也能推出初始化的d[]数组也应该全部是0

那么在一棵树上的d[x]的更新跟路径压缩怎么去弄呢？

假设目前这颗树是长这样子的

那么路径压缩后应该长这样子

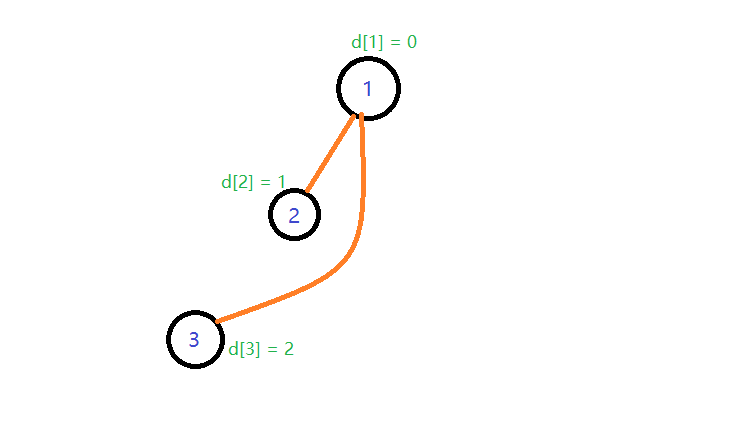
这里边发生的变化，其实就是3号节点接到了1号节点上，并且因为2号节点到1号节点的距离为1，然后3号节点到2号节点距离也是1，那么我们可以计算出3号节点到1号节点距离应该是d[2] + d[3] = 2。

达成这个目的的具体步骤也不难，就是先顺着3号节点用递归方式摸到2号节点再摸到1号节点，然后又从一号节点顺着那根线回来把距离都加到手

所以，我们的查找祖宗+路径压缩的代码就如下

int find(int x)
{
    if(x == fa[x]) return x; //是祖宗就直接返回自己

    int root = find(fa[x]); //找到根节点
    d[x] += d[fa[x]]; //递归把距离一路加回来
    fa[x] = root; //把子节点接到祖宗节点上
    return root;
}

但是有个问题，两棵树合并时，也就是一个队插到另一个队的后面时，这个d怎么去更新才合适呢？

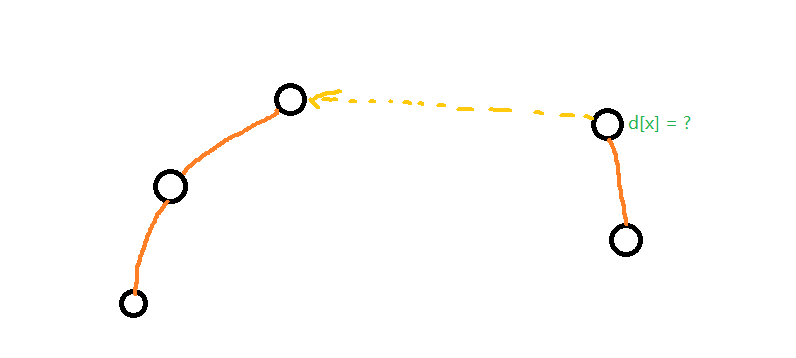
容易知道，当一个队插到另一个队的后面时，这个队的队头就排到了另一个队的队尾，那么我们就推算出这个队头到另一个队头的距离数值上等于另一个队的长度

因为涉及到队的长度，所以我们还要再引入一个信息，就是队的长度L

因为队的长度只有在两个不同的队合并时才会发生变化，所以这个L[]还是十分好维护的，就是两队长度相加即可

所以我们合并的时候，先更新祖宗d[x]再更新L[]就能达成任务了

void merge(int a, int b)
{
    if(!issame(a, b)){
        int root_a, root_b;
        root_a = find(a);
        root_b = find(b);
        d[root_a] = l[root_b];
        l[root_b] += l[root_a];
        fa[root_a] = root_b;
    }
}

查找、路径压缩以及合并，并查集的这些功能就水到渠成了

之后用就行

---

贴上AC代码

#include<iostream>
#include<algorithm>
using namespace std;

const int Maxn = 3e4 + ;
int fa[Maxn];
int l[Maxn];
int d[Maxn];

int find(int x)
{
    if(x == fa[x]) return x; //是祖宗就直接返回自己

    int root = find(fa[x]); //找到根节点
    d[x] += d[fa[x]]; //递归把距离一路加回来
    fa[x] = root; //把子节点接到祖宗节点上
    return root;
}

bool issame(int a, int b)
{
    return find(a) == find(b);
}

void merge(int a, int b)
{
    if(!issame(a, b)){
        int root_a, root_b;
        root_a = find(a);
        root_b = find(b);
        d[root_a] = l[root_b];
        l[root_b] += l[root_a];
        fa[root_a] = root_b;
    }
}

int Query(int a, int b)
{
    if(a == b) return ;
    if(issame(a, b)) return abs(d[a] - d[b]) - ;

    return -;
}

int main()
{
    for(int i=; i<Maxn ;i++){
        fa[i] = i;
        l[i] = ;
    }

    int m;
    cin>>m;
    while(m--){
        char op;
        int i, j;
        cin>>op>>i>>j;
        if(op == 'M') merge(i, j);
        else cout<<Query(i, j)<<endl;
    }

    return ;
}