[Ctsc2014]图的分割

[Ctsc2014]图的分割

阅读理解好题

翻译一下：

M(C)就是C这个诱导子图最小生成树最大边权

结论：

按照w进行sort，如果满足w<=Ci，Cj表示u,v的连通块的诱导子图

并且Ci!=Cj那么进行连边

证明：

只需要证明两点：

1.某个边如果现在需要连边（不连就不满足半完美定义），那么以后也一定需要连边

也即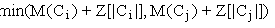，不能<=w

Z是不单调的，但是一直是正整数，而之后再进行合并，w越来越大，M(Ci)一定会一直>=w

所以不会更小

2.某个边如果现在连上了边，那么以后也不可能可以断开。

本质和1一样的。。。

所以这个构造方法一定是正确的！

#include<bits/stdc++.h>
#define reg register int
#define il inline
#define fi first
#define se second
#define mk(a,b) make_pair(a,b)
#define numb (ch^'0')
#define pb push_back
#define solid const auto &
#define enter cout<<endl
#define pii pair<int,int>
using namespace std;
typedef long long ll;
template<class T>il void rd(T &x){
    char ch;x=;bool fl=false;
    while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true);
    for(x=numb;isdigit(ch=getchar());x=x*+numb);
    (fl==true)&&(x=-x);
}
template<class T>il void output(T x){if(x/)output(x/);putchar(x%+'');}
template<class T>il void ot(T x){if(x<) putchar('-'),x=-x;output(x);putchar(' ');}
template<class T>il void prt(T a[],int st,int nd){for(reg i=st;i<=nd;++i) ot(a[i]);putchar('\n');}

namespace Miracle{
const int N=+;
const int M=+;
int n,m;
struct node{
    int a,b,w;
    bool friend operator <(node a,node b){
        return a.w<b.w;
    }
}e[M];
int fa[N],sz[N],mx[N];
int z[N];
int fin(int x){
    return fa[x]==x?x:fa[x]=fin(fa[x]);
}
vector<int>mem[N];
int main(){
    rd(n);rd(m);
    for(reg i=;i<=n;++i) rd(z[i]);
    for(reg i=;i<=m;++i){
        rd(e[i].a);rd(e[i].b);rd(e[i].w);
    }
    sort(e+,e+m+);
    for(reg i=;i<=n;++i){
        fa[i]=i;sz[i]=;
    }
    for(reg i=;i<=m;++i){
        int x=e[i].a,y=e[i].b;
        int k1=fin(x),k2=fin(y);
        if(k1!=k2){
            if(e[i].w<=min(mx[k1]+z[sz[k1]],mx[k2]+z[sz[k2]])){
                fa[k1]=k2;
                sz[k2]+=sz[k1];
                mx[k2]=e[i].w;
            }
        }
    }
    int cnt=;
    for(reg i=;i<=n;++i){
        int k=fin(i);
        if(!mem[k].size()) ++cnt;
        mem[k].push_back(i);
    }
    printf("%d\n",cnt);
    for(reg i=;i<=n;++i){
        if(mem[i].size()){
            printf("%d ",mem[i].size());
            for(reg j=;j<(int)mem[i].size();++j){
                printf("%d ",mem[i][j]);
            }
            puts("");
        }
    }
    return ;
}

}
signed main(){
    Miracle::main();
    return ;
}

/*
   Author: *Miracle*
*/