JOISC2014 Day2 E "交朋友" （思维+假的SCC）

传送门

题目描述
你是活跃在历史幕后的一名特工，为了世界和平而夜以继日地努力着。
这个世界有N个国家，编号为1..N;
你的目的是在这N个国家之间建立尽可能多的友好关系。
你为了制定一个特工工作的计划，作出了一张当今国际关系的示意图。
你准备了一张非常大的画纸，先画下了代表每个国家的N个点。
接下来，为了表示现在的国际关系，画下了M个连接两个国家的有向边;
其中从国家u连向国家v的有向边，表示国家u向国家v派遣了大使，下文称作边(u,v)。
这样就做出了N个点M条边的当今国际关系示意图。

作为两国友好关系的开端，两国之间需要进行「友好条约缔结会议」，以下简称会议。
如果某两个国家p和q要进行会议，那么需要一个向两国都派遣了大使的国家x作为中介。
会议结束后，会议的双方相互向对方的国家派遣大使。
换句话说，为了让国家p和国家q进行会议，必须存在一个国家x满足边(x,p)和边(x,q)都存在;
并且在会议后添加两条边(p,q)和(q,p)（如果需要添加的某条边已经存在则不添加）。
你的工作是对于可以进行会议的两国，选择会议的中介并促使会议进行。
使用这张图进行工作的模拟的话，世界距离和平还有多远的一个重要的基准就是这张图上的边数。

现在给出国家的个数以及当今国际关系的情报，请你求出反复选择两个国家，促使它们进行会议后，图上最多会有多少条边。

输入
第一行两个空格分隔的整数N和M，分别表示世界上国家的个数和图中的边数。
接下来M行描述画纸上的有向边的信息，其中第i行有两个空格分隔的整数ai和bi，表示图中有一条从ai到bi的有向边。

输出
输出一行一个整数，表示能实现的边数的最大值。
注意这个边数包括原有的边数和新连接的边数。

题目描述

样例输入

样例输出

样例解释
国家1作为中介国，国家2与3开会。
国家4作为中介国，国家3与5开会。
国家3作为中介国，国家2与5开会。

样例输入输出

数据范围：1≤N≤10⁵,1≤M≤2×10⁵,1≤a_i,b_i≤N，a_i≠b_i，(a_i,b_i)≠(a_j,b_j)

参考资料：

　　[1]:http://icpc.upc.edu.cn/blog/?p=108

题意（摘抄自[1]）：

　　如果存在有向边<a,b>和<a,c>,就添加两条有向边<b,c>和<c,b>(已经存在就不添加),问最多有多少条边；

题解：

　　昨天比赛做这道题的时候，想到了SCC，但我真的用SCC了，中间过程处理的不好（代码写搓了，逃）........

　　今天晚上补这道题，看了看题解，和昨天自己想的差不多，就是代码实现上，[1]并没有用SCC知识用SCC思考这道题的做法；

　　哎，欠缺的还是太多了，理解了将近半个小时，终于理解了，tql；

　　下面谈谈我的进一步理解：

　　（看会专业课先，理解明天写，下周要考两门，orz）

　　对于某节点 u，如果 u 有 > 1 个儿子 v₁,v₂ ,.......,v_x，那么 v₁,v₂ ,.......,v_x  及其所有儿子可构成强连通；

　　例如：

　　

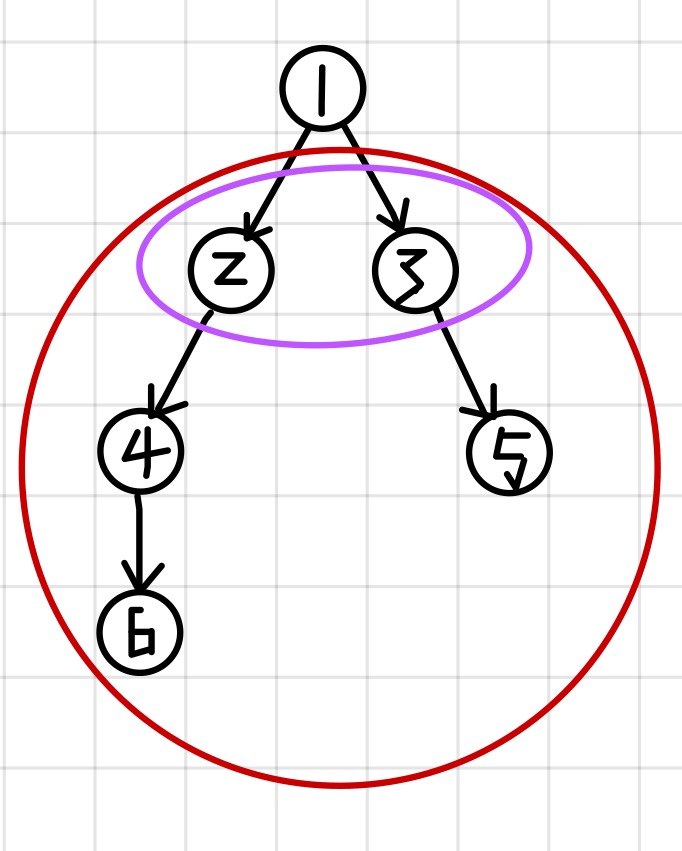
　　节点①有两个儿子②③，那么②及其所有儿子④⑥，③及其所有儿子⑤构成强连通；

　　即②③④⑤⑥构成强连通；

　　同属于同一个强连通的所有节点的信息可以集中到一个节点上，假设这5个节点的信息集中到节点②上；

 int fa[maxn];///fa[i]:i所处的强连通的代表节点
 ll tot[maxn];///tot[i]:i所处的强连通的个数，只有代表节点的tot[i]才有意义

　　fa初始化为-1,tot初始化为1；

　　对于上图，合并后的信息为：

　　fa[2]=-1,fa[3,4,5,6]=2;

　　tot[2]=5;(只有②节点的tot有用)

　　那么，最重要的就是合并操作，具体如下：

 int Find(int x)///查找x所处的强连通的代表节点
 {
     return fa[x] == - ? x:fa[x]=Find(fa[x]);
 }
 void DFS(int u,int x)
 {
     for(int i=head[u];~i;i=G[i].next)
     {
         int y=G[i].to;

         y=Find(y);
         if(x == y)
             continue;

         fa[y]=x;
         tot[x] += tot[y];
         DFS(y,x);
     }
 }

 ///合并
 bool update=true;
 while(update)
 {
     update=false;
     for(int u=;u <= n;++u)
     {
         ///判断u是否已经处于某个强连通中
         ///如果u处于某个强连通中，x=u，反之x=-1
         int x=tot[Find(u)] ==  ? -:u;
         for(int i=head[u];~i;i=G[i].next)
         {
             /**
                 如果u不处于某个强连通中：
                     ①如果其包含>1个儿子节点，其儿子节点可以构成强连通
                 如果u本身就处于某个强连通中：
                     ①其所有儿子全部在这个强连通中
             */
             int y=G[i].to;
             if(x == -)
                 x=y;
             else///将强连通中的节点信息合并到Find(x)中
             {
                 x=Find(x);
                 y=Find(y);

                 if(x == y)///在同一个强连通中
                     continue;

                 update=true;
                 fa[y]=x;
                 tot[x] += tot[y];
                 DFS(y,x);///将y的所有儿子节点合并到Find(x)中
             }
         }
     }
 }

AC代码（偷偷换成了我的风格）：

 #include<bits/stdc++.h>
 using namespace std;
 #define ll long long
 #define memF(a,b,n) for(int i=0;i <= n;a[i]=b,++i);
 const int maxn=1e5+;

 int n,m;
 int num;
 int head[maxn];
 struct Edge
 {
     int to;
     int next;
 }G[maxn<<];
 void addEdge(int u,int v)
 {
     G[num]={v,head[u]};
     head[u]=num++;
 }
 int fa[maxn];///fa[i]:i所处的强连通的代表节点
 ll tot[maxn];///tot[i]:i所处的强连通的个数，只有代表节点的tot[i]才有意义
 int Find(int x)///查找x所处的强连通的代表节点
 {
     return fa[x] == - ? x:fa[x]=Find(fa[x]);
 }
 void DFS(int u,int x)
 {
     for(int i=head[u];~i;i=G[i].next)
     {
         int y=G[i].to;

         y=Find(y);
         if(x == y)
             continue;

         fa[y]=x;
         tot[x] += tot[y];
         DFS(y,x);
     }
 }
 ll Solve()
 {
     memF(fa,-,n);
     memF(tot,,n);
     bool update=true;
     while(update)
     {
         update=false;
         for(int u=;u <= n;++u)
         {
             ///判断u是否已经处于某个强连通中
             ///如果u处于某个强连通中，x=u，反之x=-1
             int x=tot[Find(u)] ==  ? -:u;
             for(int i=head[u];~i;i=G[i].next)
             {
                 /**
                     如果u不处于某个强连通中：
                         ①如果其包含>1个儿子节点，其儿子节点可以构成强连通
                     如果u本身就处于某个强连通中：
                         ①其所有儿子全部在这个强连通中
                 */
                 int y=G[i].to;
                 if(x == -)
                     x=y;
                 else///将强连通中的节点信息合并到Find(x)中
                 {
                     x=Find(x);
                     y=Find(y);

                     if(x == y)///在同一个强连通中
                         continue;

                     update=true;
                     fa[y]=x;
                     tot[x] += tot[y];
                     DFS(y,x);///将y的所有儿子节点合并到Find(x)中
                 }
             }
         }
     }

     ll ans=;
     for(int u=;u <= n;++u)
     {
         if(fa[u] == -)
             ans += tot[u]*(tot[u]-);
         for(int i=head[u];~i;i=G[i].next)
         {
             int x=Find(u);
             int y=Find(G[i].to);
             if(x != y)
                 ans++;
         }
     }

     return ans;
 }
 void Init()
 {
     num=;
     memF(head,-,n);
 }
 int main()
 {
     scanf("%d%d",&n,&m);
     Init();
     for(int i=;i <= m;++i)
     {
         int u,v;
         scanf("%d%d",&u,&v);
         addEdge(u,v);
     }
     printf("%lld\n",Solve());

     return ;
 }