DFT与IDFT
【转】https://blog.csdn.net/mingzhuo_126/article/details/88044390

二.编程实现
考滤到DFT和IDFT算法过程中有部分相似,可以把它们合成到一个算法。
/*
x-存放要变换数据的实部
y-存放要变换数据的虚部
a-存放变换结果的实部
b-存放变换结果的虚部
n-数据长度
sign-为1时执行DFT,为-1时执行IDFT
*/
#include "math.h"
void dft(x,y,a,b,n,sign)
int n, sign;
double x[],y[],a[],b[];
{
int i,k;
double c,d,q,w,s;
q = 6.28318530718/n;
for (k=;k<n;k++)
{
w=k*q;
a[k]=b[k]=0.0;
for(i=;i<n;i++)
{
d=i*w;
c=cos(d);
s=sin(d)*sign;
a[k]+=c*x[i] + s*y[i];
b[k]+=c*y[i] - s*x[i];
}
}
if(sign == -)
{
c=1.0/n;
for (k=;k<n;k++)
{
a[k]=c*a[k];
b[k]=c*b[k];
}
}
}
下面验证此算法,对X(n)=(0,1,2,3,4,5,6,7),做DFT和IDFT算法
dft_d.c
#include "stdio.h"
#include "math.h"
#include "dft.c"
#define N 4
static double x[N],y[N],a[N],b[N],c[N];
main(){
int k;
int i=;
for(i=; i<N; i++)
{
x[i]=i;
y[i]=; }
dft(x,y,a,b,N,); //DFT变换
for(i=; i<N; i++)
{
c[i]=sqrt(a[i]*a[i]+b[i]*b[i]); //算出模
printf("%lf + j %lf \n",a[i],b[i]);//输出变换后结果
printf("%lf \n",c[i]); //输出模值
printf("\n");
}
dft(a,b,x,y,N,-); //IDFT变换
for(i=; i<N; i++)
{
printf("%lf \n",x[i]); //输出x(n)的实部
} }
运行结果:
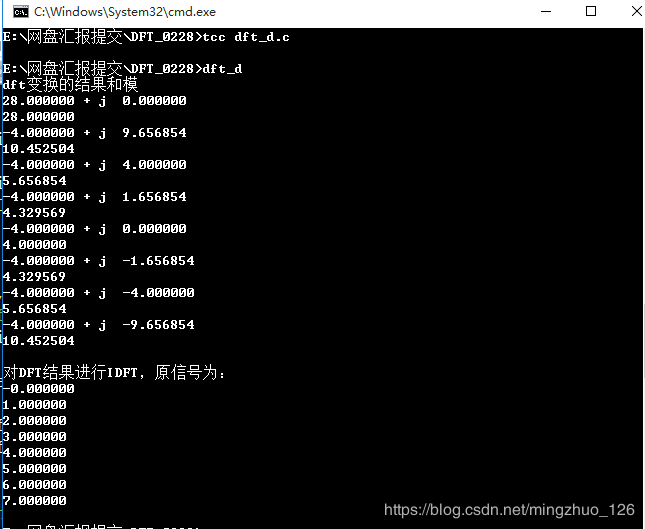
DFT与IDFT的更多相关文章
- 基2时域抽取FFT、IFFT的C++实现代码,另附DFT与IDFT的原始实现--转1
介绍网络上的原理介绍非常丰富,具体请自行搜索网络资源. 本算法依靠FFT流图进行布置. 算法 ##进行完所有的原理推导后,我们可以得到如下的16点FFT流图: 通过上图可以看出整个流图输入序列的顺序已 ...
- 信号处理之DFT、IDFT
一.DFT之前言部分 由于matlab已提供了内部函数来计算DFT.IDFT,我们只需要会调用fft.ifft函数就行: 二.函数说明: fft(x):计算N点的DFT.N是序列x的长度,即N=len ...
- 初探 FFT/DFT
有用的学习链接&书籍 傅立叶变化-维基百科 离散傅立叶变化-维基百科·长整数与多项式乘法 维基百科看英文的更多内容&有趣的图 快速傅立叶变化-百度百科,注意其中的图! 组合数学(第4版 ...
- 傅里叶变换 - Fourier Transform
傅里叶级数 傅里叶在他的专著<热的解析理论>中提出,任何一个周期函数都可以表示为若干个正弦函数的和,即: \[f(t)=a_0+\sum_{n=1}^{\infty}(a_ncos(n\o ...
- 一个蒟蒻对FFT的理解(蒟蒻也能看懂的FFT)
建议同学们先自学一下"复数(虚数)"的性质.运算等知识,不然看这篇文章有很大概率看不懂. 前言 作为一个典型的蒟蒻,别人的博客都看不懂,只好自己写一篇了. 膜拜机房大佬 HY 一. ...
- 「快速傅里叶变换(FFT)」学习笔记
FFT即快速傅里叶变换,离散傅里叶变换及其逆变换的快速算法.在OI中用来优化多项式乘法. 本文主要目的是便于自己整理.复习 FFT的算法思路 已知两个多项式的系数表达式,要求其卷积的系数表达式. 先将 ...
- 拆系数FFT
学习内容:国家集训队2016论文 - 再谈快速傅里叶变换 模板题:http://uoj.ac/problem/34 1.基本介绍 对长度为L的\(A(x),B(x)\)进行DFT,可以利用 \[ \b ...
- FFT学习笔记
快速傅里叶变换FFT(Fast Fourior Transform) 先说一下它能干嘛qwq 傅里叶变换有两种,连续傅里叶变换和离散傅里叶变换,OI中主要用来快速计算多项式卷积. 等一下,卷积是啥 ...
- FFT什么的
目录 多项式 多项式加法 多项式乘法 多项式的表示 系数表达 点值表达 系数形式表示的多项式的快速乘法 DFT&FFT&IDFT 单位复数根 DFT FFT IDFT 多项式乘法 蝶形 ...
随机推荐
- javascript 容易混淆遗忘的基础知识
1. 标识符 所谓标识符,就是指变量.函数.属性的名字,或者函数的参数.标识符可以是按照下列格式规则组合起来的一或多个字符: 1.1 第一个字符必须是一个字母.下划线( _ )或 ...
- 利用sort对数字排序
sort,可排序字符串,按照ASCII码排序. 但也可以穿一个比较函数,实现比较数组内容,排序数组的功能. var arr = [40, 32, 45, 89, 93, 0, 46, 74]; var ...
- Laravel基本使用、生成Cookie、返回视图、JSON/JSONP、文件下载及重定向
https://yq.aliyun.com/ziliao/23889 1.Response篇 1.1 基本响应 最基本的HTTP响应只需在路由闭包或控制器动作中返回一个简单字符串即可,但是具体业务逻辑 ...
- 如何查看 Python 全部内置变量和内置函数?
https://jingyan.baidu.com/article/7082dc1c071649e40a89bdb8.html Python 解释器内置了一些常量和函数,叫做内置常量(Built-in ...
- python NameError: name 'raw_input' is not defined
错误:NameError: name 'raw_input' is not defined 原因出在raw_input ,python3.0版本后用input替换了raw_input 话说回来,学习p ...
- Mac下SVN基本操作和常见错误
一.基本操作 1 从服务器上下载代码 svn checkout http://xxx.xxx.xxx/xxx 2 获取最新的代码 svn update 3 提交代码 svn commit -m ...
- P1083 合并序列
题目描述 有N个单词和字符串T,按字典序输出以字符串T为前缀的所有单词. 输入格式 输入文件第一行包含一个正整数N: 接下来N行,每行一个单词,长度不超过100: 最后一行包含字符串T. 已知:1≤N ...
- Spring Boot实战之单元测试
Spring Boot实战之单元测试 本文介绍使用Spring测试框架提供的MockMvc对象,对Restful API进行单元测试 Spring测试框架提供MockMvc对象,可以在不需要客户端-服 ...
- 2018-2-13-git-合并两个仓库
title author date CreateTime categories git 合并两个仓库 lindexi 2018-2-13 17:23:3 +0800 2018-2-13 17:23:3 ...
- vue-learning:14 - js - new Vue(options)中option
new Vue(options)中option 2019-4-14 Vue的核心是数据驱动,在template中实现视图逻辑,在javascript中实现业务逻辑.要通过模板template将数据显示 ...
