SMO算法（转）

作者：[已重置]
链接：https://www.zhihu.com/question/40546280/answer/88539689
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

SMO(Sequential Minimal Optimization)是针对求解SVM问题的Lagrange对偶问题，一个二次规划式，开发的高效算法。传统的二次规划算法的计算开销正比于训练集的规模，而SMO基于问题本身的特性（KKT条件约束）对这个特殊的二次规划问题的求解过程进行优化。对偶问题中我们最后求解的变量只有Lagrange乘子 ${\vec \alpha }$ 向量，这个算法的基本思想就是每次都只选取一对 $\left( {{\alpha _i},{\alpha _j}} \right)$ ，固定 ${\vec \alpha }$ 向量其他维度的元素的值，然后进行优化，直至收敛。

SMO干了什么？
首先，整个对偶问题的二次规划表达如下：
$\begin{align} \mathop {\max }\limits_{\vec \alpha } & \quad \sum\limits_{i = 1}^n {{\alpha _i}} - \frac{1}{2}\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{\alpha _i}{\alpha _j}{y_i}{y_j}{\bf{x}}_i^T{{\bf{x}}_j}} } \\ s.t.& \quad \sum\limits_{i = 1}^n {{\alpha _i}{y_i}} = 0 \\ & \quad {\alpha _i} \ge 0, \quad i = 1,2, \ldots ,n \end{align}$
SMO在整个二次规划的过程中也没干别的，总共干了两件事：

选取一对参数 $\left( {{\alpha _i},{\alpha _j}} \right)$
固定 ${\vec \alpha }$ 向量的其他参数，将 $\left( {{\alpha _i},{\alpha _j}} \right)$ 代入上述表达式进行求最优解获得更新后的 $\left( {{\alpha _i},{\alpha _j}} \right)$

SMO不断执行这两个步骤直至收敛。

因为有约束 $\sum\limits_{i = 1}^n {{\alpha _i}{y_i}} = 0$ 存在，实际上 ${{\alpha _i}}$ 和 ${{\alpha _j}}$ 的关系也可以确定。 ${\alpha _i}{y_i} + {\alpha _j}{y_j} = C$ 这两个参数的和或者差是一个常数。
&amp;lt;img src="https://pic1.zhimg.com/071f3351b3eee2db40fea3ba944f9d7c_b.png" data-rawwidth="633" data-rawheight="274" class="origin_image zh-lightbox-thumb" width="633" data-original="https://pic1.zhimg.com/071f3351b3eee2db40fea3ba944f9d7c_r.png"&amp;gt;所以虽然宣传上说是选择了一对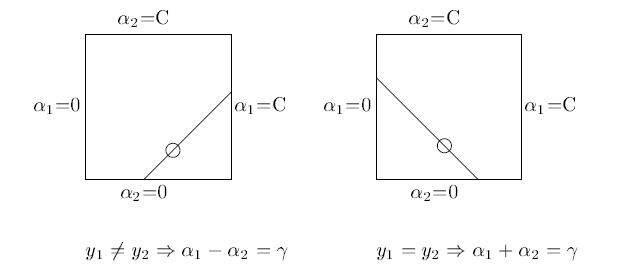

所以虽然宣传上说是选择了一对 $\left( {{\alpha _i},{\alpha _j}} \right)$ ，但还是选择了其中一个，将另一个写作关于它的表达式代入目标函数求解。

为什么SMO跑的那么快，比提出之前的算法不知道高到哪里去了？
正如上面提到的，在固定其他参数以后，这就是一个单变量二次规划问题，仅有的约束也是这个变量 $\alpha _i \ge 0$ ，显然有闭式解。不必再调用数值优化算法。

KKT条件是对偶问题最优解的必要条件：
$\begin{cases} {{\alpha _i} \ge 0}\\ {{y_i}f\left( {{{\bf{x}}_i}} \right) - 1 \ge 0}\\ {{\alpha _i}\left( {{y_i}f\left( {{{\bf{x}}_i}} \right) - 1} \right) = 0} \end{cases}$

除了第一个非负约束以外，其他约束都是根据目标函数推导得到的最优解必须满足的条件，如果违背了这些条件，那得到的解必然不是最优的，目标函数的值会减小。

所以在SMO迭代的两个步骤中，只要 $\left( {{\alpha _i},{\alpha _j}} \right)$ 中有一个违背了KKT条件，这一轮迭代完成后，目标函数的值必然会增大。Generally speaking，KKT条件违背的程度越大，迭代后的优化效果越明显，增幅越大。

怎样跑的更快？
和梯度下降类似，我们要找到使之优化程度最大的方向（变量）进行优化。所以SMO先选取违背KKT条件程度最大的变量，那么第二个变量应该选择使目标函数值增大最快的变量，但是这个变量怎么找呢？比较各变量优化后对应的目标函数值的变化幅度？这个样子是不行的，复杂度太高了。

SMO使用了一个启发式的方法，当确定了第一个变量后，选择使两个变量对应样本之间最大的变量作为第二个变量。直观来说，更新两个差别很大的变量，比起相似的变量，会带给目标函数更大的变化。间隔的定义也可以借用偏差函数
${E_i} = \max \left( {{y_i}f\left( {{{\bf{x}}_i}} \right) - 1,0} \right)$
我们要找的也就是使对于 $\alpha_i$ 来说使 $\left| {{E_i} - {E_j}} \right|$ 最大的 $\alpha_j$

很惭愧，只做了一点微小的工作。

References
[1] Platt, John. "Sequential minimal optimization: A fast algorithm for training support vector machines." (1998).

SMO算法（转）的更多相关文章

机器学习——支持向量机(SVM)之Platt SMO算法
Platt SMO算法是通过一个外循环来选择第一个alpha值的,并且其选择过程会在两种方式之间进行交替: 一种方式是在所有数据集上进行单遍扫描,另一种方式则是在非边界alpha中实现单遍扫描. 所谓 ...
支持向量机原理(四)SMO算法原理
支持向量机原理(一) 线性支持向量机支持向量机原理(二) 线性支持向量机的软间隔最大化模型支持向量机原理(三)线性不可分支持向量机与核函数支持向量机原理(四)SMO算法原理支持向量机原理(五) ...
SVM-非线性支持向量机及SMO算法
SVM-非线性支持向量机及SMO算法如果您想体验更好的阅读:请戳这里littlefish.top 线性不可分情况线性可分问题的支持向量机学习方法,对线性不可分训练数据是不适用的,为了满足函数间隔大 ...
改进的SMO算法
S. S. Keerthi等人在Improvements to Platt's SMO Algorithm for SVM Classifier Design一文中提出了对SMO算法的改进,纵观SMO ...
[笔记]关于支持向量机（SVM）中 SMO算法的学习（一）理论总结
1. 前言最近又重新复习了一遍支持向量机(SVM).其实个人感觉SVM整体可以分成三个部分: 1. SVM理论本身:包括最大间隔超平面(Maximum Margin Classifier),拉格朗日 ...
关于SVM数学细节逻辑的个人理解（三）：SMO算法理解
第三部分:SMO算法的个人理解接下来的这部分我觉得是最难理解的?而且计算也是最难得,就是SMO算法. SMO算法就是帮助我们求解: s.t. 这个优化问题的. 虽然这个优化问题只剩下了α这一个变 ...
支持向量机(Support Vector Machine)-----SVM之SMO算法(转)
此文转自两篇博文有修改序列最小优化算法(英语:Sequential minimal optimization, SMO)是一种用于解决支持向量机训练过程中所产生优化问题的算法.SMO由微软研究院的 ...
支持向量机（五）SMO算法
11 SMO优化算法(Sequential minimal optimization) SMO算法由Microsoft Research的John C. Platt在1998年提出,并成为最快的二次规 ...
机器学习之支持向量机（二）：SMO算法
注:关于支持向量机系列文章是借鉴大神的神作,加以自己的理解写成的:若对原作者有损请告知,我会及时处理.转载请标明来源. 序: 我在支持向量机系列中主要讲支持向量机的公式推导,第一部分讲到推出拉格朗日对 ...
支持向量机-SMO算法简化版
SMO:序列最小优化 SMO算法:将大优化问题分解为多个小优化问题来求解 SMO算法的目标是求出一系列的alpha和b,一旦求出这些alpha,就很容易计算出权重向量w,并得到分隔超平面工作原理:每 ...

随机推荐

Java 接口 interface implements
接口定义了一系列的抽象方法和常量,形成一个属性集合. 接口定义完成后任何类都可以实现接口,而且一个类可以实现多个接口. 实现接口的类必须实现接口中定义的抽象方法,具体实现细节由类自己定义.可以说接口定 ...
【appium】根据name定位元素
目前没有尝试成功,等成功后补充个人建议可以尝试先用view显示的文本作为name看是否能拿到该控件,按照我个人的经验一般都是会成功的,所以我很怀疑安卓上面控件的name是否就等于text.
[转]Oracle中trace的几种
Oracle中trace的几种标签: 杂谈我们在Oracle中在做troubleshooting的时候,经常要去做跟踪来查错,那今天就介绍几种trace的方法. 在这之前,我先说说10046事 ...
全选,反选,获取值ajax提交
//必须先加载jquery //加载弹出框插件 artdialog http://www.planeart.cn/demo/artDialog/ /****全选反选*开始**/ $(document ...
ALGO-5_蓝桥杯_算法训练_最短路
记: 一开始没接触过关于最短距离的算法,便开始翻阅关于图的知识, 得知关于最短距离的算法有Dijkstra算法(堆优化暂未看懂),Bellman-Ford算法,Floyd算法,SPFA算法. 由于数据 ...
selenium page object模式
页面对象模式将测试代码和被测试页面的元素及操作进行分离,以降低页面元素的变化对测试代码的影响.每个被测试的页面都会被定义一个类,类中会定位元素和操作. 如果不使用page object模式,则相同的操 ...
IE6 CSS高度height:100% 无效解决方法总结
原文地址:http://www.cnblogs.com/huangyong8585/archive/2013/02/05/2893058.html 上面红色部分为 height:100%; 自动拉 ...
1037 Magic Coupon （25 分）
1037 Magic Coupon (25 分) The magic shop in Mars is offering some magic coupons. Each coupon has an i ...
javascript继承之组合继承(三)
function Father(name) { this.name = name; } Father.prototype.say = function () { return this.name; } ...
Hibernate cascade级联
cascade: 级联: 是对象的连锁操作级联保存(一对多): 级联保存: 当保存双向关系的一方时,默认会报告错误,此时应该在customr中设置级联保存,即操作一个对象时,通过操作其他关联对象如 ...

SMO算法（转）

SMO算法（转）的更多相关文章

随机推荐

热门专题