Andrew Ng-ML-第十四章-无监督学习

1.无监督学习概述

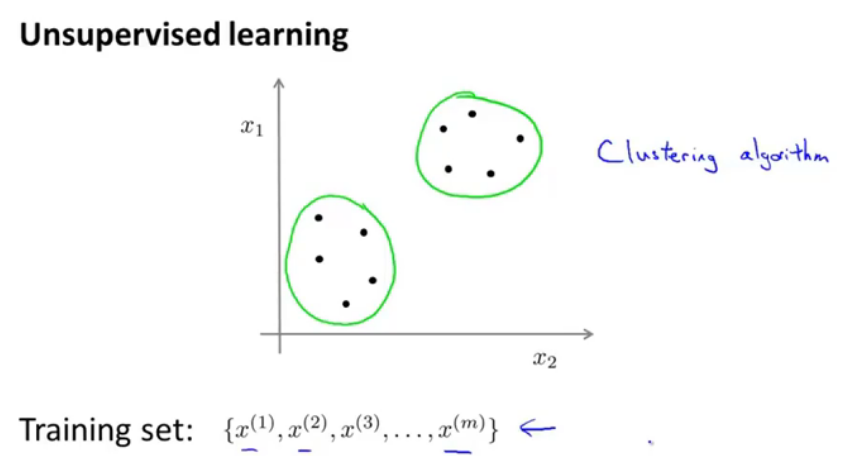
 图1.无监督学习

有监督学习中，数据是有标签的，而无监督学习中的训练集是没有标签的，比如聚类算法。

2.k-means算法

k-means算法应用是十分广泛的聚类方法，它包括两个过程，首先是选取聚类中心，然后遍历每一个点，决定其属于哪个类；第二步是移动聚类中心点，根据刚才的聚类情况将聚类中心点移动，下面三个图很好地说明了这个过程：

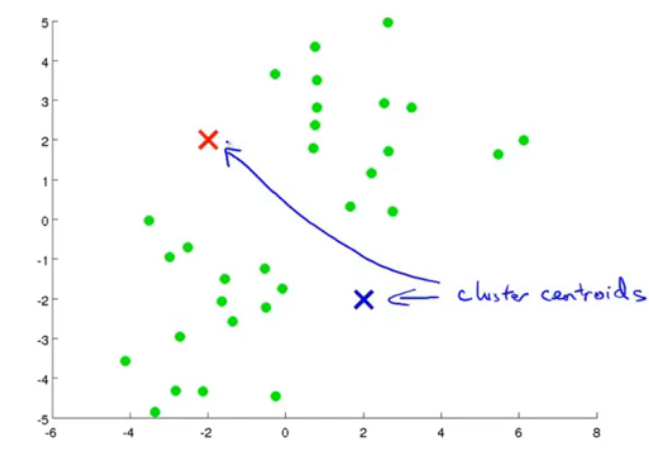
图2.初始化，并且计算距离。

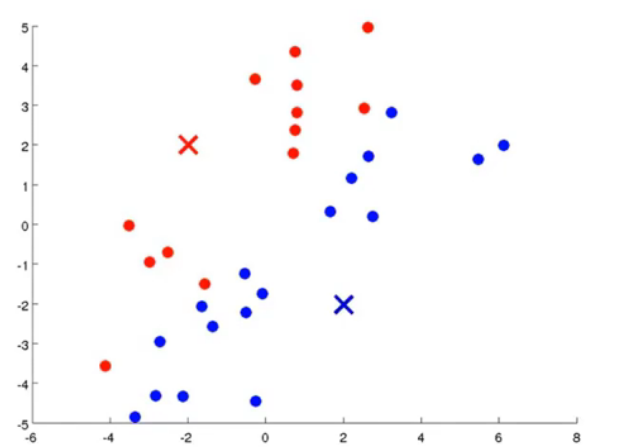
图3.计算距离后

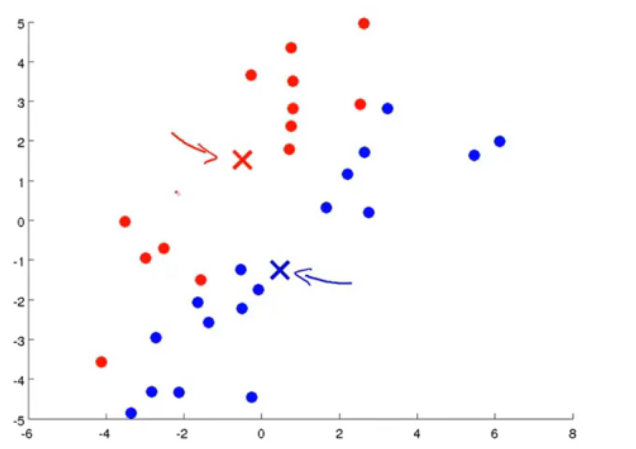
图4.根据最小化均方误差移动聚类中心点

根据新的聚类中心点，再次重复这个过程，

图5.迭代之后最终结果

迭代之后最终结果，就算再运行k-means聚类算法，聚类中心点也不会改变了，

图6.k-means算法输入

输入包括k，之后会讲解如何选择k，训练集，x(i)是n维的，不是n+1维，通常舍去x_0=1项。

图7.k-means算法过程

K是指一共分为几簇，k是指每个聚类中心。

首先随机初始化k各聚类中心点，循环以下过程：

1.将m个样本点遍历，分到k个聚类中心中；

2.根据各个簇中的点到聚类中心点的距离并取均值。

对于聚类结果中，没有点的簇，通常是直接删去，那么K就变成了K-1簇。

3.优化目标

图8.k-means优化目标

就是最小化代价函数，也叫失真代价函数。优化目标就是使点到聚类中心的平均距离最小。

4.随机初始化

这节会讲如何避开局部最优。

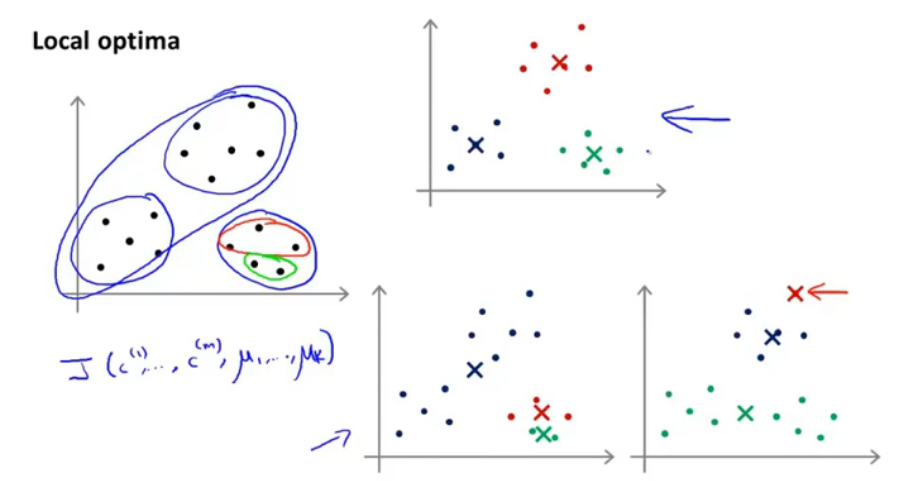
图9.局部最优化情况

如图就是局部最优化情况，两个类被分成了一个簇，一个簇被分开成了两份，这是不好的，是因为聚类中心店的初始化的问题。解决办法就是初始化多次，并且运行多次k-means聚类算法，得到结果，保证得到一个足够好的结果。

图10.运行局部最优化算法

随机初始化，重复k-means算法100次，通常是在50-1000之间，运行结束后，选取一个失真函数最小的聚类结果。

随机初始化的情况，适用于K在2-10之间，多次随机初始化会比较好的得到正确的聚类结果，但是当不在此区间内，聚类结果并不会有很大的改善，K很大时一次聚类结果即可。

5.选择簇的数量

目前来说，还都是通过可视化的方法手动选择的。

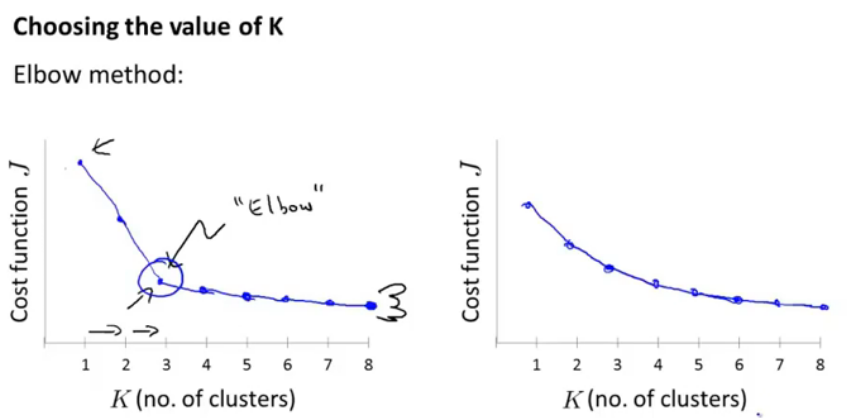
图11.如何选择聚类K的值

选择K个聚类的值，并以损失函数为纵轴来判断，肘形函数，但是有时会像有部，是平滑的，也不好确定最终分为几类，所以这个肘形曲线并不能成为好的判断方法。

但是最终的应用结果会告诉你应该分为几类。