字符串匹配算法——BF、KMP、Sunday

一：Brute force

从源串的第一个字符开始扫描，逐一与模式串的对应字符进行匹配，若该组字符匹配，则检测下一组字符，如遇失配，则退回到源串的第二个字符，重复上述步骤，直到整个模式串在源串中找到匹配，或者已经扫描完整个源串也没能够完成匹配为止。

缺点：假如我们从头开始匹配str1和str2，当匹配到str1[i]时，发现str2[i]！=str1[i]，这时我们就回到str1起始匹配的地方，把str2右移一位，对准str1下一字符作为起点，进行匹配。由于上一次匹配到了str1[i]，那么重新开始匹配时，新匹配起点~str1[i]这段子串又要被重新匹配。

二：KMP

暴力搜索的缺点在于单纯地从原来匹配起点右移一位重新匹配，效率低下并且没有好好利用上一次匹配时得出的有效信息。

KMP算法的出发点为：从上一次匹配过程中，检测出有效信息，使下一次匹配不是单纯地右移一位开始匹配，而是跳过一段不必要尝试的子串，直接从下一有可能匹配成功的起点开始匹配。

概念准备：

前缀：字符串A = "abcde"，那么a,ab,abc,abcd,abcde都是A的前缀，前缀其实就是字符串A从左往右、从头开始依次取长度为1、2、3...str.length()的子串。

后缀：字符串A = "abcde"，那么abcde,bcde,cde,de,e都是A的后缀，同理，后缀就是依次从A的开头、第二位，第三位...最后一位开始截取，取到尾部的子串。

真前缀、真后缀：即不等于字符串本身的前缀、后缀子串。

kmp算法的核心:

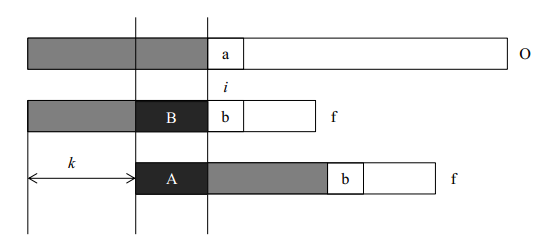
计算字符串f每一个位置之前的子串的前缀和真后缀公共部分的最大长度（不包括子串本身，否则最大长度始终是子串本身）。当每次比较到两个字符串的字符不同时，我们就可以根据当前比较位置的最大公共长度将字符串f右移(已匹配长度-最大公共长度)位，重新开始匹配。

我们把查找的字符串成为模式串，KMP算法的代码实际上分两部分：

1：预处理模式串，得到next[]数组（next数组为：对于模式串的每一位j，当位j与主串不匹配时，模式串下一个匹配起点是模式串中的哪位）；【相对移动，这里不求最大长度和模式串右移多少位，而是直接求模式串右移后，新的匹配的起点的位置（因为右移后，前缀是匹配的，所以不是从模式串开头进行匹配，而是从前缀的后一位开始）】

2：匹配字符串，每当匹配到不相同位时，使用next[]得到模式串下一个用来匹配的起点；

 public static int[] next(char[] t) {
        int[] next = new int[t.length];
        next[0] = -1;
        int i = 0;
        int j = -1;
        while (i < t.length - 1) {
            if (j == -1 || t[i] == t[j]) {
                i++;
                j++;
                if (t[i] != t[j]) {
                    next[i] = j;
                } else {
                    next[i] = next[j];
                }
            } else {
                j = next[j];
            }
        }
        return next;
    }  

 public static int KMP_Index(char[] s, char[] t) {
        int[] next = next(t);
        int i = 0;
        int j = 0;
        while (i <= s.length - 1 && j <= t.length - 1) {
            if (j == -1 || s[i] == t[j]) {
                i++;
                j++;
            } else {
                j = next[j];
            }
        }
        if (j < t.length) {
            return -1;
        } else
            return i - t.length; // 返回模式串在主串中的头下标
    }  

三：Sunday

简单、快速的匹配算法。

思路如下：摘自：http://blog.csdn.net/laojiu_/article/details/50767615

假设我们有如下字符串：
A = "LESSONS TEARNED IN SOFTWARE TE";
B = "SOFTWARE";
Sunday算法的大致原理是：
先从左到右，两个字符串逐个字符比较，i指向主串下标，j指向模式串下标；
开始的时候，我们让i = 0, 指向A的第一个字符; j = 0 指向B的第一个字符，分别为"L"和"S"，不等；这个时候，找到位于A字串中位于B字符串长度后面的第一个字符，下标为m，即下图字符"T"，然后在模式字符串B中从后向前查找是否存在"T"；

可以看到下图模式串的T，下标为k；

将相等的字符对齐（对齐的方法为：令i移动，j仍指向模式串开头）：

再次比较A[i]和B[j]，不等，这时再次寻找主串中在模式串后面的那个字符，

我们看到，模式串的最后一个字符与m指向的主串字符相等，再次对齐

这时，主串i对应的字符是S，j对应的子串字符也是S。则逐位比较，同步移动下标：i++, j++

现在再次不等，找到A中的m，指向字符"D"，

代码实现：

    //从后向前寻找目标字符下标
    private int contains(char[] chars,char target){
        for(int i = chars.length-1 ; i >= 0; i--){
            if(chars[i] == target){
                return i ;
            }
        }
        return -1;
    }

   //sunday算法
    public int Sunday(String dest , String pattern){

        char[] destchars = dest.toCharArray();
        char[] patternchars = pattern.toCharArray();

        int i = 0;
        int j = 0;
        //控制边界
        while(i <= (dest.length() - pattern.length() + j )  ){
            if( destchars[i] != patternchars[j] ){//对应位不相同
                if(i == (dest.length() - pattern.length() + j )){//已经末尾对齐
                    return -1;
                }
                //还未到主串末尾，则继续下面操作
                //在模式串中。查找主串中对应模式串末尾的下一位字符在模式串中的下标
                int pos = contains(patternchars,destchars[i+pattern.length()-j]);
                if( pos== -1){//若没有，则直接把模式串对齐末尾的下一位
                    i = i + (pattern.length()  - j)+1;
                    j = 0 ;
                }else{
                    i = i + (pattern.length() - j)-pos;
                    j = 0;
                }
            }else{//对应位相同
                if(j == (pattern.length() - 1)){//如果对应位已经到达模式串末尾，则匹配成功
                  return  i-j+1;
                }else{//未到末尾，则比较下一位
                    i++;
                    j++;
                }
            }
        }
    }