【BZOJ1502】[NOI2005]月下柠檬树 Simpson积分

【BZOJ1502】[NOI2005]月下柠檬树

Description

李哲非常非常喜欢柠檬树，特别是在静静的夜晚，当天空中有一弯明月温柔地照亮地面上的景物时，他必会悠闲地坐在他亲手植下的那棵柠檬树旁，独自思索着人生的哲理。李哲是一个喜爱思考的孩子，当他看到在月光的照射下柠檬树投在地面上的影子是如此的清晰，马上想到了一个问题：树影的面积是多大呢？李哲知道，直接测量面积是很难的，他想用几何的方法算，因为他对这棵柠檬树的形状了解得非常清楚，而且想好了简化的方法。李哲将整棵柠檬树分成了n 层，由下向上依次将层编号为1,2,…,n。从第1到n-1 层，每层都是一个圆台型，第n 层(最上面一层)是圆锥型。对于圆台型，其上下底面都是水平的圆。对于相邻的两个圆台，上层的下底面和下层的上底面重合。第n 层(最上面一层)圆锥的底面就是第n-1 层圆台的上底面。所有的底面的圆心(包括树顶)处在同一条与地面垂直的直线上。李哲知道每一层的高度为h1,h2,…,hn，第1 层圆台的下底面距地面的高度为h0，以及每层的下底面的圆的半径r1,r2,…,rn。李哲用熟知的方法测出了月亮的光线与地面的夹角为alpha。

 

为了便于计算，假设月亮的光线是平行光，且地面是水平的，在计算时忽略树干所产生的影子。李哲当然会算了，但是他希望你也来练练手

Input

第1行包含一个整数n和一个实数alpha，表示柠檬树的层数和月亮的光线与地面夹角(单位为弧度)。

第2行包含n+1个实数h0,h1,h2,…,hn，表示树离地的高度和每层的高度。

第3行包含n个实数r1,r2,…,rn，表示柠檬树每层下底面的圆的半径。

上述输入文件中的数据，同一行相邻的两个数之间用一个空格分隔。

输入的所有实数的小数点后可能包含1至10位有效数字。

1≤n≤500，0.3<alpha<π/2，0<hi≤100，0<ri≤100

Output

输出1个实数，表示树影的面积。四舍五入保留两位小数。

Sample Input

2 0.7853981633
10.0 10.00 10.00
4.00 5.00

Sample Output

171.97

题解：简洁题意就是让你求一堆圆和梯形的面积交。

Simpson积分：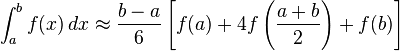  

相当于用一个3次函数去拟合所求的图形，可以用于任意连续不规则图形，但是误差很大。自适应simpson积分呢，就是再对f(l,mid)和f(mid,r)分别算一下。如果f(l,mid)+f(mid,r)与f(l,r)误差很小，则直接返回f(l,r)，否则继续递归计算。这样误差就比较小了（虽说也可以卡）。

剩下的问题就是如何求两圆的公切线。比较容易的方法是设两圆半径为R,r，先令R'=R-r,r'=0，这样就把第二个圆缩成了一个点，变成求点与圆的切线，再平移回去即可。

#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <iostream>
#define pi acos(-1.0)
using namespace std;
typedef double db;
const db eps=1e-6;
int n,m;
db alpha,h[510],O[510],R[510],ax[510],ay[510],bx[510],by[510];
inline db f(db x)
{
	db ret=0;
	int i;
	for(i=1;i<=n;i++)	if(x>=O[i]-R[i]&&x<=O[i]+R[i])
		ret=max(ret,sqrt(R[i]*R[i]-(O[i]-x)*(O[i]-x)));
	for(i=1;i<=m;i++)	if(x>=ax[i]&&x<=bx[i])
		ret=max(ret,ay[i]+(by[i]-ay[i])*(x-ax[i])/(bx[i]-ax[i]));
	return ret;
}
inline db simpson(db a,db b)
{
	return (b-a)/6*(f(a)+f(b)+f((a+b)/2)*4);
}
inline db calc(db l,db r,db val)
{
	db mid=(l+r)/2,a=simpson(l,mid),b=simpson(mid,r);
	if(fabs(a+b-val)<eps)	return val;
	return calc(l,mid,a)+calc(mid,r,b);
}
int main()
{
	scanf("%d%lf",&n,&alpha);
	int i;
	db l=1e9,r=-1e9;
	for(i=0;i<=n;i++)
	{
		scanf("%lf",&h[i]),h[i]/=tan(alpha);
		if(i)	h[i]+=h[i-1];
	}
	for(i=1;i<=n;i++)
	{
		scanf("%lf",&R[i]),O[i]=h[i-1],l=min(l,O[i]-R[i]),r=max(r,O[i]+R[i]);
		if(i!=1&&O[i]-O[i-1]>fabs(R[i]-R[i-1]))
		{
			db a=(R[i-1]-R[i])/(O[i]-O[i-1]),b=sqrt(1-a*a);
			ax[++m]=O[i-1]+a*R[i-1],ay[m]=b*R[i-1];
			bx[m]=O[i]+a*R[i],by[m]=b*R[i];
		}
	}
	if(h[n]>O[n]+R[n])
	{
		db a=R[n]/(h[n]-O[n]),b=sqrt(1-a*a);
		r=h[n];
		ax[++m]=O[n]+a*R[n],ay[m]=b*R[n];
		bx[m]=h[n],by[m]=0;
	}
	printf("%.2lf",calc(l,r,simpson(l,r))*2);
	return 0;
}//2 0.7853981633 10.0 10.00 10.00 4.00 5.00