用人工智能模型预测股市和加密货币的K线图

前一篇：《从爱尔兰歌曲到莎士比亚：LSTM文本生成模型的优化之旅》

前言：加密货币市场昨日大幅下跌，一天内市值蒸发逾70亿 人民币。有人可能会问，如果使用人工智能模型预测市场的涨跌，是否能避免损失？作者在此指出，加密货币市场和股市具有高度的主观性，受人为因素、情绪波动和外界干预的显著影响，而非单纯依赖客观规律。因此，即便人工智能能够基于历史数据和市场规律做出客观预测，也无法避免因市场主观性而导致的不确定性或偏差。因此，在主观决策时不要让人工智能帮你来做。

理解序列和时间序列数据

时间序列无处不在。你可能在天气预报、股票价格以及像摩尔定律这样的历史趋势中见过它们（见图9-1）。如果你不熟悉摩尔定律，它预测微芯片上的晶体管数量大约每两年翻一番。近50年来，它已被证明是预测计算能力和成本未来变化的准确指标。

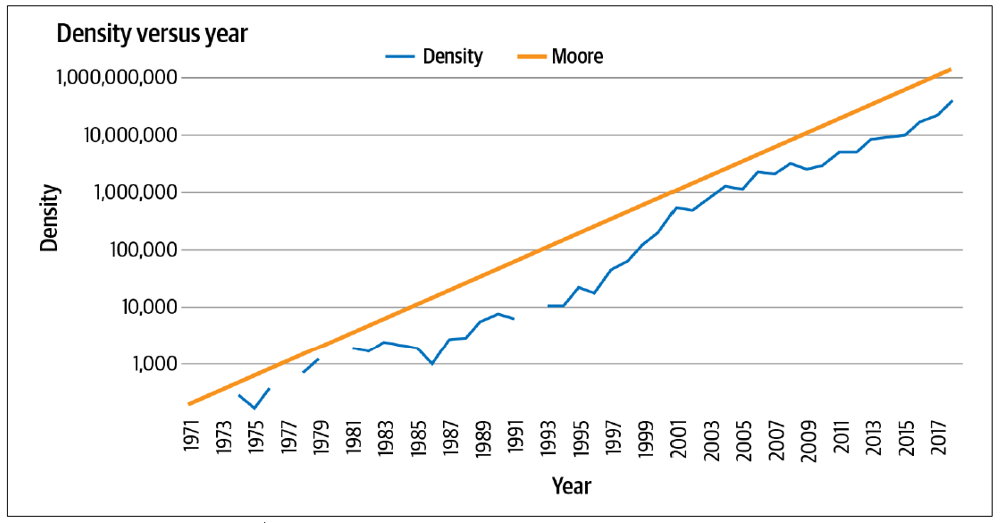
                                            图9-1. 摩尔定律

时间序列数据是一组随时间间隔变化的数值。当绘制时，x轴通常是时间轴。时间轴上常常绘制多个数值，例如在这个例子中，一个是晶体管数量的图，另一个是根据摩尔定律预测的值。这叫做多变量时间序列。如果只有一个数值——比如降水量随时间的变化——那就叫做单变量时间序列。

对于摩尔定律，预测比较简单，因为有一个固定且简单的规则，可以大致预测未来——这个规则已经有效了大约50年。

但是像图9-2中的时间序列呢？

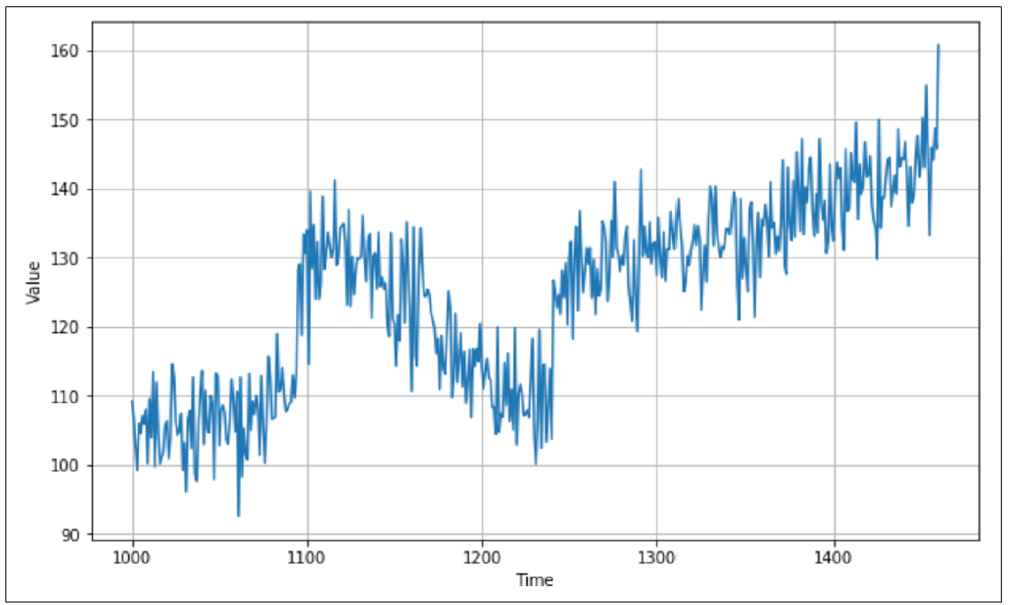
图9-2. 真实世界的时间序列

虽然这个时间序列是人工创建的（你稍后会看到如何做），它具备了复杂的真实世界时间序列的所有特征，比如股票图表或季节性降水。尽管看起来像是随机的，时间序列实际上有一些共同的特征，这些特征在设计可以预测它们的机器学习模型时非常有用，正如下一节所描述的那样。

时间序列的常见特征

虽然时间序列看起来可能是随机和噪声的，但通常它们有一些可预测的共同特征。在这一节，我们将探讨其中的一些特征。

趋势

时间序列通常会朝着特定的方向发展。在摩尔定律的例子中，很容易看出，随着时间的推移，y轴上的值在增加，呈现上升趋势。图9-2中的时间序列也有一个上升趋势。当然，这并不总是如此：有些时间序列可能会随着时间的推移大致保持平稳，尽管有季节变化，而其他一些则呈下降趋势。例如，摩尔定律的反向版本就预测了每个晶体管的价格下降趋势。

季节性

许多时间序列会呈现出一种随时间重复的模式，这种重复会以定期的间隔发生，称为季节性。比如，考虑天气中的温度。我们通常每年有四个季节，夏季温度最高。如果你将几年的天气数据绘制出来，你会看到每四个季节会出现一个峰值，这就是季节性的概念。但这种现象并不仅限于天气。例如，图9-3就是一个网站流量的图。

图9-3. 网站流量

这是按周绘制的，你可以看到规律性的下降。你能猜到是什么原因吗？这个网站提供的是软件开发者的信息，正如你所预料的那样，周末流量较少！因此，时间序列显示了五天高流量和两天低流量的季节性。数据是在几个月的时间里绘制的，圣诞节和新年假期大致在中间，所以你能看到那时的额外季节性。如果我把数据绘制几年的话，你会明显看到年末流量的下跌。

季节性可以以多种方式在时间序列中呈现。例如，零售网站的流量可能在周末达到峰值。

自相关

时间序列中的另一个特征是事件发生后会出现可预测的行为。在图9-4中，你可以看到明显的尖峰，但每次尖峰后都会出现一种确定性的衰减。这就叫做自相关。

在这种情况下，我们能看到一种特定的行为模式，这种模式会重复出现。自相关可能隐藏在时间序列的模式中，但它们具有内在的可预测性，因此包含许多自相关的时间序列可能是可以预测的。

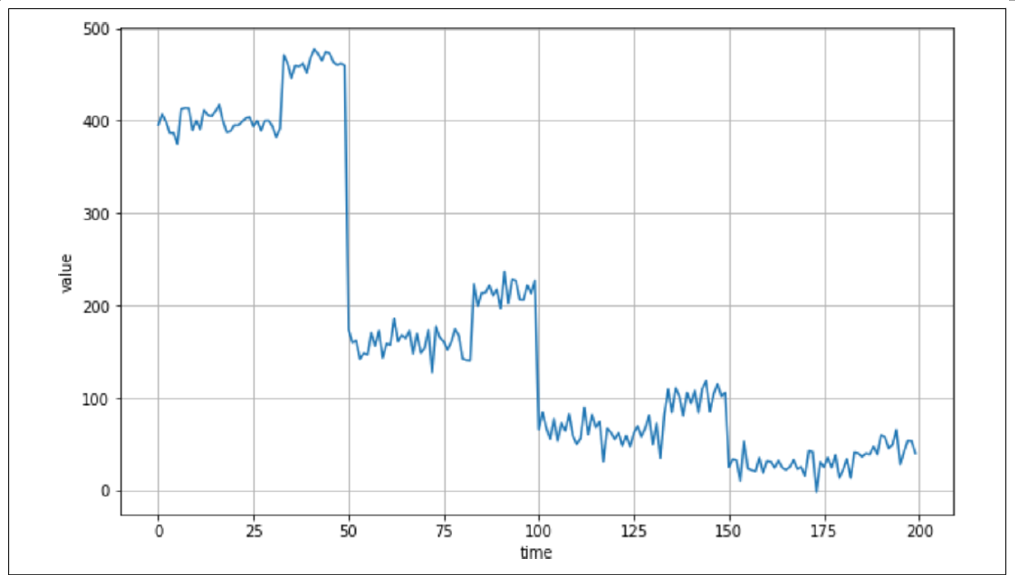
                                      图9-4. 自相关

噪声

顾名思义，噪声是时间序列中看似随机的扰动。这些扰动导致了高度的不确定性，并且可能掩盖趋势、季节性行为和自相关。例如，图9-5展示了与图9-4相同的自相关图，但加上了一些噪声。突然间，看到自相关的情况变得更加困难，预测值也变得更难。

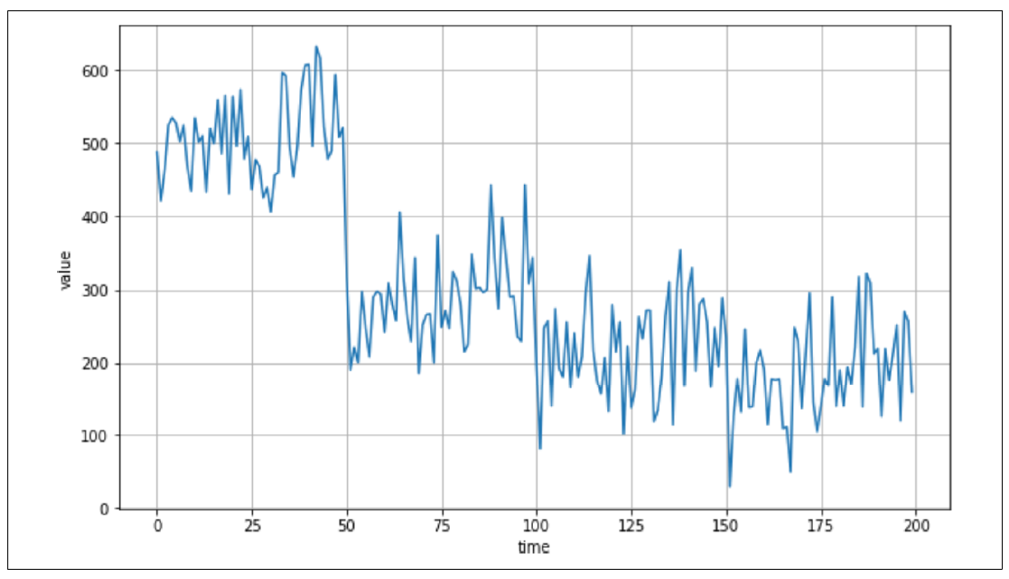
图9-5. 加入噪声的自相关序列

考虑到这些因素，我们来探讨一下如何对包含这些特征的时间序列进行预测。

总结：今天的内容主要为大家介绍了序列的概念。通过摩尔定律的简单示例，我们了解了时间序列的定义和基本特征，比如趋势、季节性、自相关和噪声。实际生活中，股市的K线图、加密货币价格走势，以及网站流量波动，都是典型的时间序列。这些特征帮助我们更好地理解数据变化的规律，为后续的机器学习模型应用提供了方向。下一篇将详细介绍如何利用人工智能模型或机器学习技术来预测和生成序列数据。