回溯算法————n皇后、素数串

回溯就是算法是搜索算法中一种控制策略，是一个逐个试探的过程。在试探的过程中，如果遇到错误的选择，就会回到上一步继续选择下一种走法，一步一步的进行直到找到解或者证明无解为止。

如下是一个经典回溯问题n皇后的解答树：

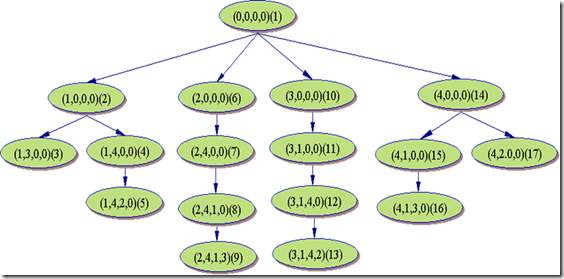
下面就从n皇后说起：

---

【问题描述】

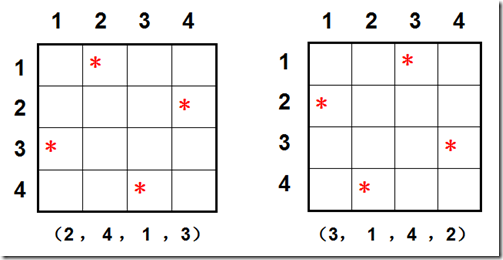
在n×n的国际象棋盘上，放置n个皇后，使任何一个皇后都不能吃掉另一个,需满足的条件是：同一行、同一列、同一对角线上只能有一个皇后。求所有满足要求的放置方案。4皇后的放置方案如下：

【输入】一个正整数n。

【输出】每行代表一种放置方案：第i行的第一个数是i，表示第i种方案，后面一个冒号，然后是用空格隔开的n个数，其中第i个数x[i]表示第i行上的皇后放在第x[i]列；最后一行：一个整数，表示方案总数。

【样例输入】

4

【样例输出】

1:2 4 1 3

2:3 1 4 2

2

这个题目简直是太经典了，一提到回溯第一个想到的就是它。这个题非常的通俗易懂，就是在一个n*n的棋盘上满足条件地放置n个皇后，每种组合搜一遍就好了。在搜的过程中判断下一步的某种方向是否可以走，如果可以的话就进入下一层，如果不符合要求就搜下一个方向，搜完这一层的所有方向以后就回到上一层，继续搜上一层的下一个方向。

不知道大家看懂了没有，如果没看懂，看代码就懂了。。

上代码：

#include<iostream>
#include<cstdio>

using namespace std;

int n;
int sum=0;//解法存放个数
int a[100000];//存放皇后位置数据
bool b[1000000]={0},c[1000000]={0},d[10000000]={0};//b存储y方向,c、d存储对角线

void print()
{
	sum++;
	cout<<sum<<':';
	for(int i=1;i<=n;i++)
	{
		cout<<a[i]<<' ';
	}
	cout<<endl;
}

int search(int x)
{
	for(int j=1;j<=n;j++)//遍历本层中每种方向
	{
		if((!b[j])&&(!c[x+j])&&(!d[x-j+n-1]))//如果满足条件
		{
			a[x]=j;//存入皇后数据
			b[j]=1;//占领y轴
			c[x+j]=1;//占领对角线
			d[x-j+n-1]=1;//占领对角线
			if(x==n)
			{
				print();//如果有完整解，输出
			}
			else
			{
				search(x+1);//如果没有继续找下一行
			}
			b[j]=0;//找完之后取消占领
			c[x+j]=0;
			d[x-j+n-1]=0;
		}
	}
}

int main()
{
	cin>>n;
	search(1);//从第一个开始找
	cout<<sum;
}

　　把思想带到代码里应该就看懂了吧。

回溯就是这样一层一层的找，找完本层返回上一层继续找，直到找到正确解为止。

继续再看一道题：

3、素数链

设计程序将1。。。n排成一排，使任意两个相邻的数的和为素数。第1个和最后一个的和也为素数.输出一种方案即可。

输入：

n （n<=100）

输出:

1到n的一个序列，中间用一个空格隔开。第一个数为1。

如果无解输出-1。

样例输入：

10

样例输出：

1  2  3  4  7  6  5  8  9  10

这道题和刚才那道n皇后的思路是一样的，遍历所有可能，在遍历的过程中判断，如果可以就继续搜下一层。

代码如下：

#include<cstdio>
#include<iostream>

const int maxx=1000;

using namespace std;

int n;
int numguo[maxx]={0};
bool guo[maxx]={0},pguo=0;
int c=0;

int sushu(int x)//验证素数的函数
{
//关于判断素数的题很早就做过，这里我就不解释了
	int i=2;
	while(i<x)
	{
		if(x%i==0)
		return 0;//如果不是直接跳出返回0
		i++;
	}
	return 1;//如果是的话返回1
}

int panduan()
{
	int t;
	for(int i=1;i<n;i++)//判断是否达到要求
	{
		if(!sushu(numguo[i]+numguo[i+1]))//这里我直接放到函数里去验证
		{
			return 0;//如果不是素数就直接跳出返回0
		}
	}
	if(!sushu(numguo[n]+numguo[1])) return 0;//注意别忘了最后一个和第一个数字的和是否为素数
	return 1;//正确的话返回1
}

int print()
{
	c++;//可能方法+1
	for(int i=1;i<=n;i++){
		cout<<numguo[i]<<' ';
	}
	cout<<endl;
}

int search(int x)
{
	for(int i=1;i<=n;i++)//搜索本层中每种可能
	{
		if(!guo[i])
		{
			guo[i]=1;//占领
			numguo[x]=i;//标记
			if(x==n)//如果达到数量要求
			{

				if(panduan())//如果符合要求
				{
					if(!pguo)//如果没输出过
					{
						pguo=1;//输出过
						print();//输出
						return 0;//搜到就直接跳出
					}
				}
			}
			else search(x+1);
			guo[i]=0;
			numguo[x]=0;
		}
	}
}

int main()
{
	cin>>n;
	search(1);//从第一个开始找
	if(!c)	cout<<"-1";//如果没可能就输出“-1”
	return 0;
}

　　这些代码中我用了很多的函数，这样节约了代码长度，也更加方便（个人觉得）。

回溯就是这个中心思想，一步步往下搜，一层层的搜，直到搜完或找到结果为止。

其实上面两道题都是很水的基础，再往后还有回溯遍历图、树等等等等。。

ending。。。