主成分分析、实例及R语言原理实现

欢迎批评指正！

主成分分析（principal component analysis，PCA）

一。几何的角度理解PCA -- 举例：将原来的三维空间投影到方差最大且线性无关的两个方向（二维空间）。

二。数学推导的角度为 -- 将原矩阵进行单位正交基变换。

且听我慢慢展开。

关于第一句话，给个图直观理解，请问，下面的三维空间中的一条鱼，在二维平面时怎么能更直观的看出，这是一条鱼？

很明显，第一种情况更直观，为什么呢？

这就是将原矩阵（三维空间）投影到了信息量最大的两个维度上（二维平面），这就是PCA所做的事情，降维

参考https://www.bilibili.com/medialist/play/ml304203591

　　https://www.matongxue.com/madocs/228/

关于第二句话，从数学的角度解释，一句话，原矩阵进行单位正交基变化。

首先。什么是基变化

举例

三维空间中的四个点（矩阵B），左乘一个矩阵A，没有发生任何变化，因为该矩阵就是B的基，如果A发生变化，对应的乘积也发生变化。

第二，为什么要正交单位基，单位基很好理解了，就是为了计算的方便，正交的目的是为了PCA降维之后，我们希望能对各个主成分进行合理解释，如果非正交的话，各主成分之间相关性很高，结果难已解释。

下面到了最重要的一点，如何找鸡？不对不对，找基！

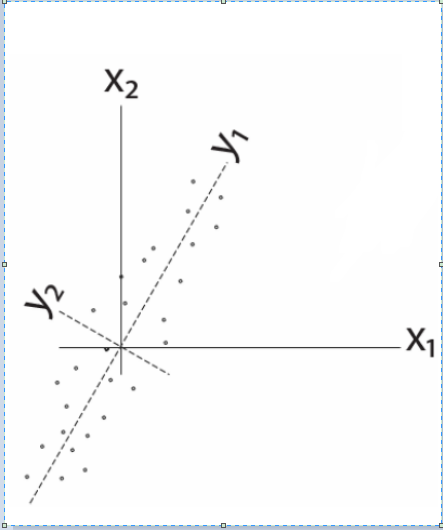
当我们遇到这样的（左面）的数据时，我们很难去选择将数据投影到X1或者X2，因为两个基上的数据信息量差别不大，我们希望找到像Y1,Y2这样的基，这时的取舍就很明确了。

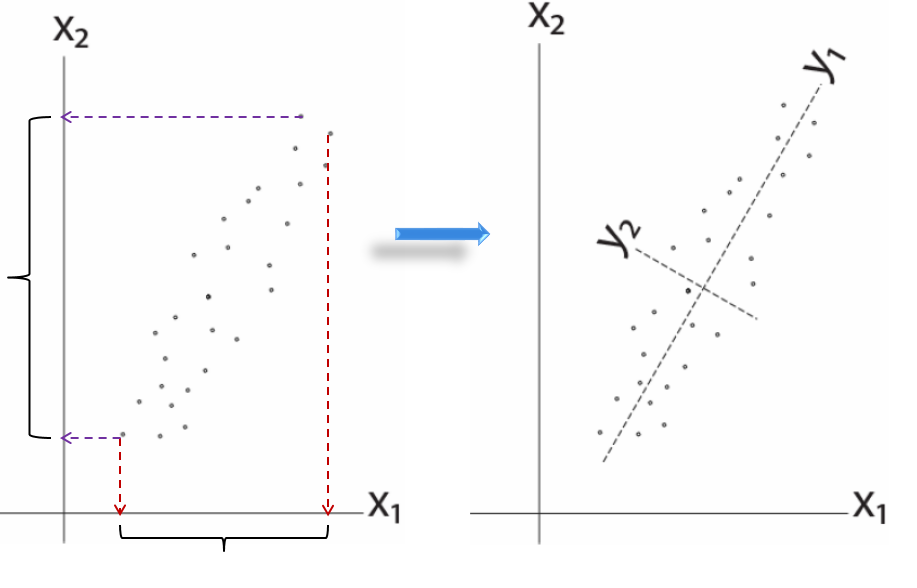
首先，我们将数据中心化

疑问（问什么要中心化）

因为标准化之后X的相关矩阵等于协方差阵，证明（忽视角标0_0），注意此处的Y与下文的Y无关

因为在之前X坐标系下，X1与X2存在很大的相关性，所义无法很好的选择一个维度来投影，但是在Y坐标系下，Y1,Y2之间相关性很小，投影方向很明确。

问题转化为Y = PX,

那么我们希望得到的是一个除去对角线上元素为1之外的其他元素均为零的矩阵。

第三步为谱分解，她有很好的性质，如，Q为X的特征向量组，为单位正交矩阵，D为对角线元素为X特征值的对角线矩阵

对于第④步的解释：我们希望得到的是Y的协方差矩阵为对角线矩阵，而D为对角线矩阵，PQ = 单位矩阵即可，

又Q为正交阵，所以inverse Q = transpose Q，所以

我们可以选择特征值较大的eigenvectors 乘以 X，实现降维

伪代码

实例及R语言实现

a <- c(-1,-1,0,2,0)
b <- c(-2,0,0,1,1)
x <- as.matrix(cbind(a,b))   # already normalization
x
cor <- cor(x)
eig <- eigen(cor)
plot(eig$values)
p <- eig$vectors
y <- t(p) %*% t(x)
plot(t(y))

参考https://www.bilibili.com/video/av29441413/?p=3

https://www.bilibili.com/medialist/play/ml304203591

https://blog.csdn.net/y521263/article/details/44925363