Harmonic Number（调和级数+欧拉常数）

In mathematics, the nth harmonic number is the sum of the reciprocals of the first n natural numbers:

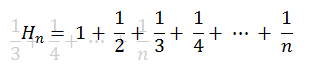
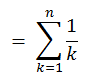
In this problem, you are given n, you have to find Hn.

Input
Input starts with an integer T (≤ 10000), denoting the number of test cases.

Each case starts with a line containing an integer n (1 ≤ n ≤ 108).

Output
For each case, print the case number and the nth harmonic number. Errors less than 10-8 will be ignored.

Sample Input
12

1

2

3

4

5

6

7

8

9

90000000

99999999

100000000

Sample Output
Case 1: 1

Case 2: 1.5

Case 3: 1.8333333333

Case 4: 2.0833333333

Case 5: 2.2833333333

Case 6: 2.450

Case 7: 2.5928571429

Case 8: 2.7178571429

Case 9: 2.8289682540

Case 10: 18.8925358988

Case 11: 18.9978964039

Case 12: 18.9978964139

题意：求f(n)=1/1+1/2+1/3+1/4…1/n   (1 ≤ n ≤ 108).，精确到10^-8。

题解：当n很小时，可直接求出结果，当n很大时，利用公式f(n)=ln(n)+C+1/(2*n)，在C++ math库中，log即为ln;

代码：

#include <iostream>
#include <cstdio>
#include <cmath>
using namespace std;
const double r=0.57721566490153286060651209;//欧拉常数
double a[];
int main()
{
    a[]=;
    for (int i=;i<;i++){//预先把小于10000的f(n)求出来
        a[i]=a[i-]+1.0/i;
    }
    int n; cin>>n;
    for (int kase=;kase<=n;kase++)
    {
        cin>>n;
        if (n<){//n<10000时，可直接得出结果
            printf("Case %d: %.10lf\n",kase,a[n]);
        }
        else{//否则利用欧拉公式
            double a=log(n)+r+1.0/(*n);
            printf("Case %d: %.10lf\n",kase,a);
        }
    }
    return ;
}