leetcode69 X的平方根的几种解法

第一种自然就是调APi啦(手动滑稽)

public int mySqrt(int x) {
        return (int)Math.sqrt(x);
    }

时间是52 ms,还超过了1/5的人呢

第二种 二分法

就是在0--X之间一半地一半地砍,最后直到左右边界的中间的数 = X/mid,这样做是防止因为mid数字太大而导致溢出

看代码吧,跟排序类似

public int getSqrtByDevide(int x) {
        if (x<=1) {
            return x;
        }
        int low = 0;
        int high = x;
        int mid = 0;
        while(low<=high) {
            mid = low + (high - low)/2;
            if(mid == (x/mid))
                return mid;
            else if(mid < (x/mid))
                low = mid + 1;
            else
                high = high -1;
        }
        return high;
    }

这种比上种稍微快一点:45 ms

第三种 牛顿迭代法

刚开始还没搞懂是怎么回事,后来看了网上的一些帖子才明白.

首先拿此题来说,假设最后的输出的结果x² = N,(N是函数参数终点x),这里可以看成一个函数,即f(x) = x² - N;

那么最终的目的就变成了求这个函数的零点了

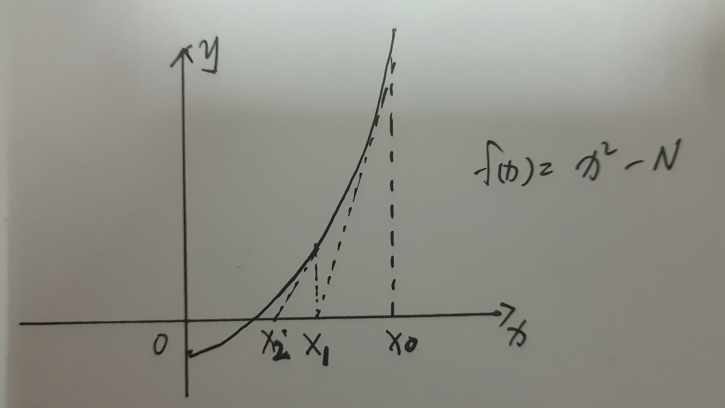
迭代过程就是从X0开始,看它的平方是不是等于N,是就返回,不是就在X0对应的在函数图像上的点上做切线

再求这个切线和x轴的交点,重复上面的步骤:

f(x) = x² - N
设点Xi,则经过点(Xi,f(Xi))处的切线方程为g(x) = f(Xi)+ f'(Xi)(x - Xi)
令g(x) = 0
得x = Xi - f(Xi)/f'(Xi)
又f(Xi) = Xi² - N
代入得最终迭代式子:
x = (Xi + N/Xi)/2;

然后代码:

public int getSqrtByNewton(int x) {
        if (x<=1) {
            return x;
        }
        double last = -1;//最后
        double ans = 1;//结果
        while(last!=ans) {
            last = ans;//将迭代前的ans存起来,如果和迭代后ans相等,代表非常逼近
            ans = (ans+x/ans)/2;
        }
        return (int)ans;

    }

这个还是很快的:27ms

第四种 "0x5f3759df"算法

这个的原理我也没搞太清楚,好像有个专门的论文将这个算法的,很神奇,经常用于图形学游戏领域一些场景里面

那我就只贴个代码吧(凑个字数...)

public int mySqrt(int x) {
        long t = x;
    t = 0x5f3759df - (t >> 1);
    while (!(t*t <= x && (t+1)*(t+1) > x))
        t = (x/t + t)/2;
    return (int)t;
    }

这里有讲,挺麻烦的,我就知道打一波666吧...

http://www.sandaoge.com/info/new_id/30.html?author=1