网络编程基础【day09】：socket解决粘包问题之MD5（八）

本节内容

1、概述

2、代码实现

一、概述

　　上一篇博客讲到的用MD5来校验还是用的之前解决粘包的方法，就是客户端发送一个请求，等待服务端的确认的这样的一个笨方法。下面我们用另外一种方法：就是客户端已经知道可接收多少数据了，既然客户端已经知道接收多少数据了，那么客户端在接收数据的时候，正好接收已经知道的数据，不就ok了吗？就是说我循环了正好是收到已经知道的那些数据。比如：我要发5M的数据，我正好收到5M的数据，然后就不往下再收了，因为它有可能跟MD5值黏在一块了，本来说是发5M文件，结果你发了5.1M，那么客户端正好收5M的话，那客户端的0.1M是不是就不收了，不收了之后我就把客户端把文件存下来，再来recive一下，下面recive的正好是0.1M。

二、代码实现

说明：其实我们在接收文件时，只有最后一次才会超过接收大小，所以我们从这里下手

2.1、服务端代码

说明：生成md5对象->发送的数据生成MD5值->发送MD5 值

①代码

import hashlib

import socket,os

server = socket.socket()

server.bind(("localhost",9999))

server.listen()

while True:

conn,addr = server.accept()

print("new conn:",addr)

while True:

print("等待新指令")

data = conn.recv(1024)

if not data:

print("客户端已断开")

break

cmd,filename = data.decode().split()

print(filename)

if os.path.isfile(filename):

m = hashlib.md5() #生成MD5的对象

with open(filename,"rb") as f:

file_size = os.stat(filename).st_size

conn.send( str(file_size).encode() ) #send file size

conn.recv(1024)

for line in f:

m.update(line) #计算md5值

conn.send(line) #发送数据至客户端

print("file md5",m.hexdigest())

conn.send(m.hexdigest().encode()) #生成MD5值并且发送给客户端

print("send done")

server.close()

②代码改动

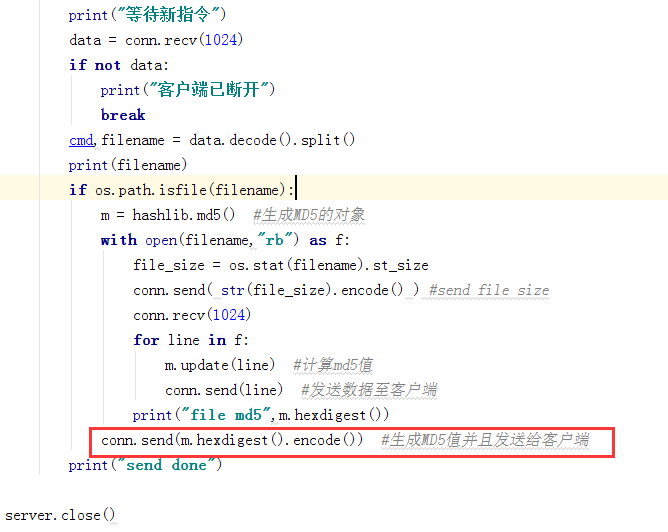
2.2、客户端

说明：文件大小-接收大小是否大于1024 ->获取size值->recive(size)->下面再次recive时就是MD5值了

①代码

import socket,hashlib

client = socket.socket()

client.connect(("localhost",9999))

while True:

cmd = input(">>>:").strip()

if len(cmd) == 0:continue

if cmd.startswith("get"):

client.send(cmd.encode())

server_respose = client.recv(1024)

print("server response:",server_respose)

client.send("ready to recv file".encode())

file_total_size = int(server_respose.decode())

revived_size = 0

filename = cmd.split()[1]

m = hashlib.md5() #生成MD5对象

with open(filename + ".new","wb") as f:

while revived_size < file_total_size:

if file_total_size - revived_size > 1024: #要收不止一次

size = 1024

else: #最后一次，剩多少收多少

size = file_total_size - revived_size

print("last receive:",size)

data = client.recv(size)

revived_size += len(data)

m.update(data) #计算数据接收的MD5值

f.write(data)

else:

print(file_total_size,revived_size)

new_file_md5 = m.hexdigest() #生成接收数据的MD5值16进制形式

server_file_md5 = client.recv(1024) #接收客户端的MD5值

print("server file md5:",server_file_md5.decode())

print("client file md5:",new_file_md5)

client.close()

②代码改动

2.3、思路图

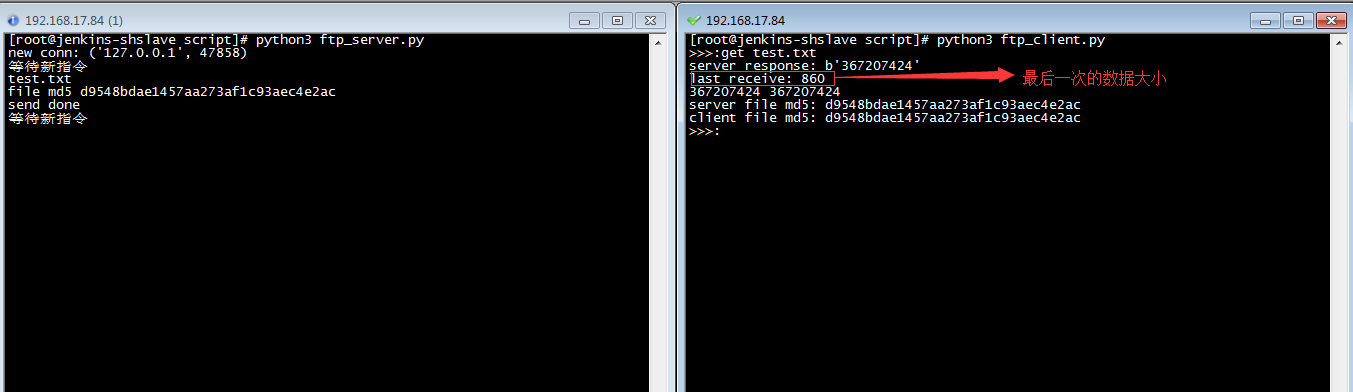
2.4、实现的效果图