BPOS关于“相邻库存查询”的调整

　　“相邻库存查询”的应用场景：主要是实现门店间，相互查看商品库存状况，但出于公司对门店的查看权限控制要求，不能一次性查看到相关店铺的所有库存，所以产生了“相邻库存查询”的功能，通过后台系统给指定门店定义相关联的店仓，让门店可以按照单款查询到的方式查询到已定义的“相邻店铺”的商品库存分布状况。

　　但是标准产品里面设计的“相邻库存查询”，因对查询条件的匹配限制(当输入“款号”能查询所有尺码的库存分布情况，输入“条码”时只能查询次条码的库存情况)，这样的方式降低“相邻看下查询”的功能效果，接收很多客户的反馈之后，重新调整自定义了相关程序(getBarcodeQtyCanByUserId_C.jsp)，添加条码解析函数(oracle数据库自定义函数get_mpda_no_mpt)，实现了扫入条码，直接查询所有尺码的库存情况。

　　

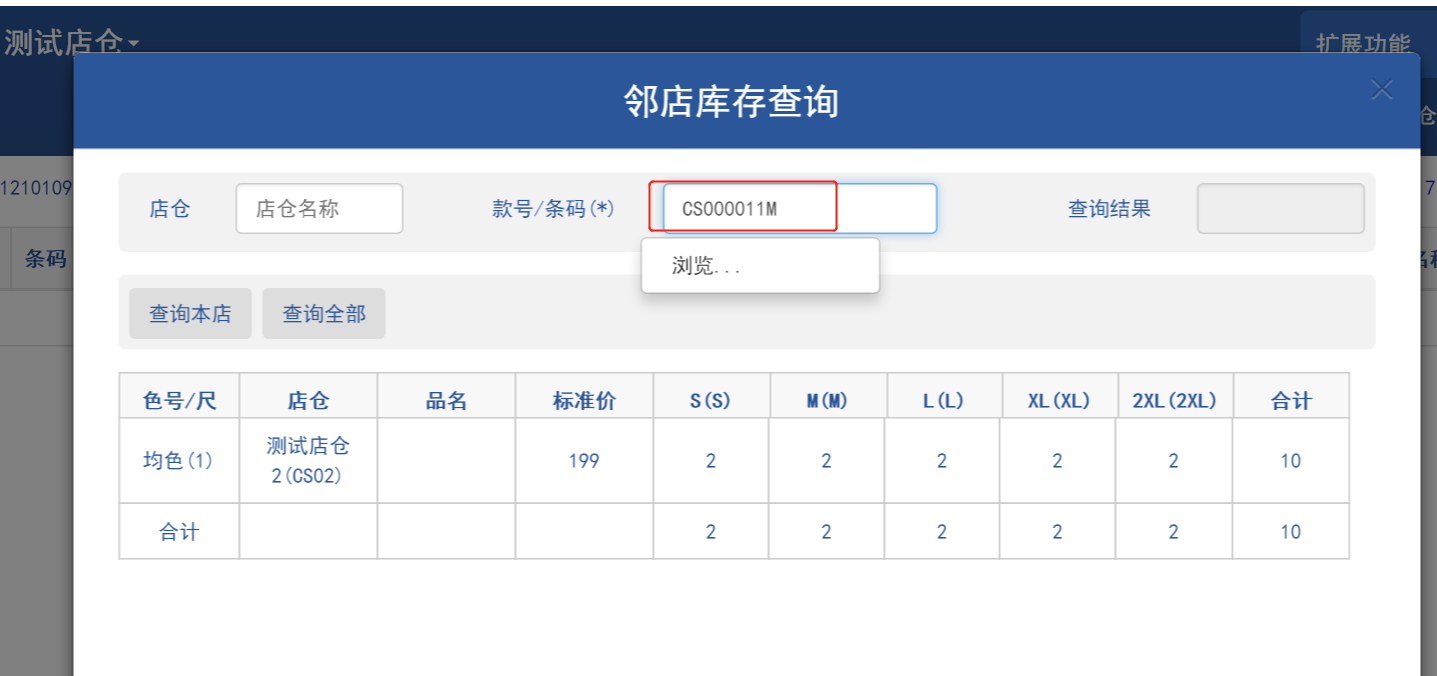
　　修改后的jsp
　　

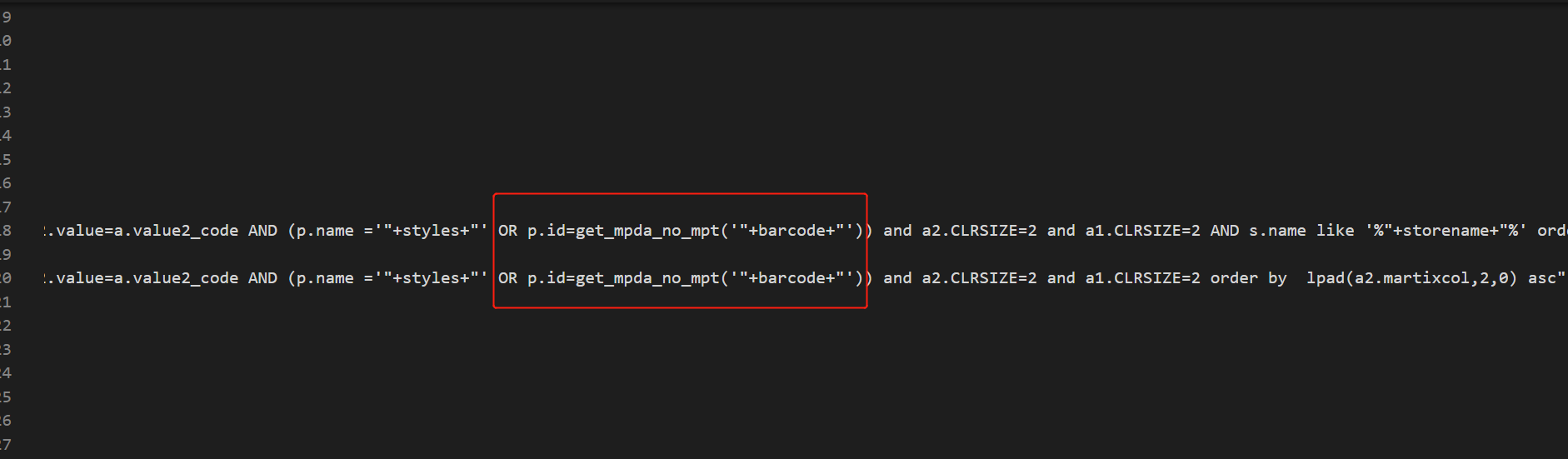
　　自定义函数get_mpda_no_mpt的代码

　　

create or replace function get_mpda_no_mpt(p_no in varchar2) return number as

  v_seqname varchar2(80);
  pos       number(10);
  m_pda_id  number(10);

begin

  --1条码
  begin
    EXECUTE IMMEDIATE '
    select t.m_product_id  from m_product_alias t where t.no = :1'
      into m_pda_id
      using p_no;

  exception
    when no_data_found then
      m_pda_id := null;
  end;
  if m_pda_id is not null then
    return m_pda_id;
  end if;

  --2条码
  begin
    EXECUTE IMMEDIATE '
    select t.id from m_product t where t.name = :1'
      into m_pda_id
      using p_no;

  exception
    when no_data_found then
      m_pda_id := null;
  end;
  if m_pda_id is not null then
    return m_pda_id;
  end if;

  --3流水码（截取位数）
  pos := ad_param_value(37, 'portal.6001', 0);
  begin
    --raise_application_error(-20201,pos);
    FOR v IN (SELECT regexp_substr(pos, '[^,]+', 1, LEVEL, 'i') AS text
                FROM dual
              CONNECT BY LEVEL <=
                         length(pos) - length(REPLACE(pos, ',')) + 1) LOOP
      EXECUTE IMMEDIATE 'select max(m_product_id) from m_product_alias where no=:1'
        INTO m_pda_id
        USING substr(p_no, 1, length(p_no) - v.text);
      IF m_pda_id > 0 THEN
        return m_pda_id;
      END IF;
    END LOOP;
  exception
    when no_data_found then
      m_pda_id := null;
  end;
  if m_pda_id is not null then
    return m_pda_id;
  end if;

  --4国标码
  begin
    EXECUTE IMMEDIATE '
    select t.m_product_id
      from m_product_alias t
     where t.INTSCODE = :1'
      into m_pda_id
      using p_no;
  exception
    when no_data_found then
      m_pda_id := null;
  end;
  if m_pda_id is not null then
    return m_pda_id;
  end if;

  --5新旧条码对照
  begin
    EXECUTE IMMEDIATE '
    select a.m_product_id
      from m_pdt_alias_con t, m_product_alias g,m_product_alias a
     where t.m_pda_old_id = g.id
     and t.m_pda_new_id=a.id
       and g.no = :1'
      into m_pda_id
      using p_no;

  exception
    when no_data_found then
      m_pda_id := null;
  end;

  if m_pda_id is not null then
    return m_pda_id;
  end if;

  return m_pda_id;

end;

　　后台“相邻店铺”维护调整，标准的“相邻店铺”维护只能是一一对应维护，例如定义A店铺的“相邻店铺”为B、C店铺，则需要再A店铺的店仓档案下的“相邻店铺”table也页添加B、C店铺后，再到B、C店铺的店仓档案下添加A店铺，维护起来很是不方便。

　　解决方案：通过给店仓档案添加新的标签，修改对应的店仓档案程序，在对店仓档案修改的时候，识别将统一标签的店仓直接相互更新到对应的“相邻店铺”。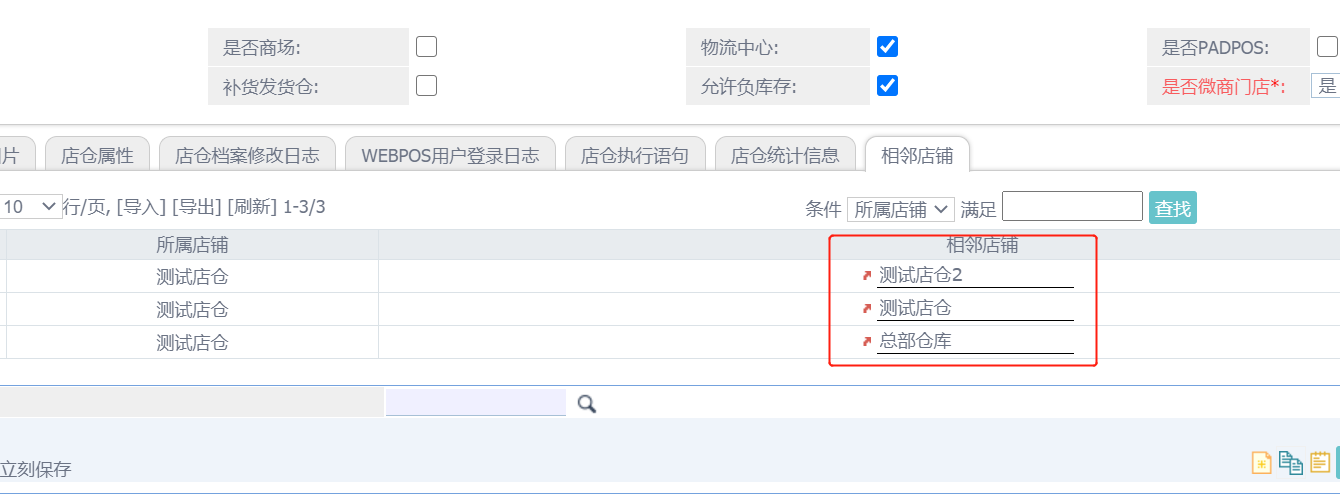

 1  /*根据店仓性质更新相邻店铺*/
 2   --先删除原明细
 3   delete from C_STORENEB;
 4
 5   for v in (select a.id, a.c_storekind_id
 6               from c_store a
 7              where a.isactive='Y') loop
 8
 9     --插入新的明细
10     insert into C_STORENEB t
11       (id,
12        ad_client_id,
13        ad_org_id,
14        c_neb_store_id,
15        c_store_id,
16        ownerid,
17        modifierid,
18        creationdate,
19        modifieddate,
20        isactive)
21       select get_sequences('C_STORENEB'),
22              a.ad_client_id,
23              a.ad_org_id,
24              a.id,
25              v.id,
26              ownerid,
27              modifierid,
28              creationdate,
29              modifieddate,
30              isactive
31         from c_store a
32        where a.isactive='Y';
33   end loop;