【ACwing 98】分形之城—

（题面来自ACwing）

城市的规划在城市建设中是个大问题。

不幸的是，很多城市在开始建设的时候并没有很好的规划，城市规模扩大之后规划不合理的问题就开始显现。

而这座名为 Fractal 的城市设想了这样的一个规划方案，如下图所示：

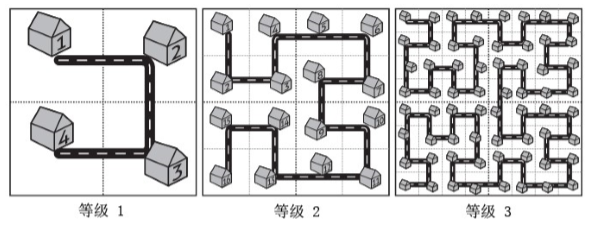
当城区规模扩大之后，Fractal 的解决方案是把和原来城区结构一样的区域按照图中的方式建设在城市周围，提升城市的等级。

对于任意等级的城市，我们把正方形街区从左上角开始按照道路标号。

虽然这个方案很烂，Fractal 规划部门的人员还是想知道，如果城市发展到了等级 N，编号为 A 和 B 的两个街区的直线距离是多少。

街区的距离指的是街区的中心点之间的距离，每个街区都是边长为 10 米的正方形。

输入格式

第一行输入正整数n，表示测试数据的数目。

以下n行，输入n组测试数据，每组一行。

每组数据包括三个整数 N,A,B, 表示城市等级以及两个街区的编号，整数之间用空格隔开。

输出格式

一共输出n行数据，每行对应一组测试数据的输出结果，结果四舍五入到整数。

数据范围

1≤N≤31,
1≤A,B≤22N,
1≤n≤1000

　　分形指的是一种无限包含更小尺度下的自身的几何结构。当然，题中的城市是有最小尺寸边界的，即n = 0时。

　　该题的难点是在这样的图中根据房屋编号找到它的坐标位置。我们发现，城市扩建只是扭转了左上、左下第n-1级城市的方向，城市本身的结构没有变化，而每个房屋旋转后的坐标是有规律的。因此，我们想要确定房屋a在第n级城市中的位置，只需要先确定出它在哪个次级的n-1级城市里，求出它在这个子城市中的坐标，然后分情况讨论这个子城市中的房屋在构成现在城市时发生的坐标变化即可。边界：n = 0时，坐标为(0, 0)。总时间复杂度为O(n * N)。确定子城市可以用编号除以子城市大小size（2的(2n-2)次方），确定a在子城市中的编号则可以用编号对size取模得到。为了这一步运算方便，我们把房屋改为从0到n-1编号。具体的坐标变化规律见代码。

　　在计算距离的时候遇到了锅，所以想强调一下数据范围。int的最大值是2^31 - 1，刚好够记录城市直径（从0行开始），但是平方级别的编号会炸。所以在记录城市尺寸、房屋编号的时候要记得开long long。

代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <climits>
#define fst first
#define sec second
#define mp make_pair
typedef long long LL;
using namespace std;
int n, T;
LL a, b;
pair<LL, LL> solve(int n, LL pos) {
if (n == 0) return mp(0, 0);
LL len = 1LL << (n - 1), size = 1LL << ((n << 1) - 2), id = pos / size;
pair<LL, LL> sub = solve(n - 1, pos % size);
LL x = sub.first, y = sub.second;
switch (id) {
case 0:
return mp(y, x);
case 1:
return mp(x, y + len);
case 2:
return mp(x + len, y + len);
case 3:
return mp((len << 1) - y - 1, len - x - 1);
default: break;
}
}
double calc(pair<LL, LL> a, pair<LL, LL> b) {//double sqrt(double x)
return sqrt((a.fst - b.fst) * 1.0 * (a.fst - b.fst) + (a.sec - b.sec) * 1.0 * (a.sec - b.sec)) * 10;
}
int main() {
scanf("%d", &T);
while (T--) {
scanf("%d %lld %lld", &n, &a, &b);
printf("%.0lf\n", calc(solve(n, --a), solve(n, --b)));
}
return 0;
}