【bzoj5110】[CodePlus2017]Yazid 的新生舞会 Treap

题目描述

求一个序列所有的子区间，满足区间众数的出现次数大于区间长度的一半。

输入

第一行2个用空格隔开的非负整数n,type，表示序列的长度和数据类型。数据类型的作用将在子任务中说明。

第二行n个用空格隔开的非负整数，依次为A1,A2,...,An，描述这个序列。

N<=500000,0<=Type<=3

对于所有数据，保证 0 ≤ Ai ≤ n - 1。

对于 type = 0 的数据，没有任何特殊约定。

对于 type = 1 的数据，保证 Ai ∈ {0, 1}。

对于 type = 2 的数据，保证序列 A 的众数在整个序列中的出现次数不超过 15。

对于 type = 3 的数据，保证 Ai ≤ 7。

输出

输出一行一个整数，表示答案。

样例输入

5 0
1 1 2 2 3

样例输出

10

---

题解

Treap

做麻烦了...

先把所有相同的数出现的位置存到一个vector里，然后考虑这个数作为众数的贡献。

考虑枚举贡献段的最后一个数的位置，这样对于某个左边的该数出现的位置，区间长度应该满足：区间长度小于2*这段中该数的个数。

如果设 x 表示右端点位置， y 表示右端点在某位置下满足条件的区间个数。那么由于区间长度一定，可以得到一个 y=-x+b 类型的直线（实际上有意义的只有第一象限的部分）。

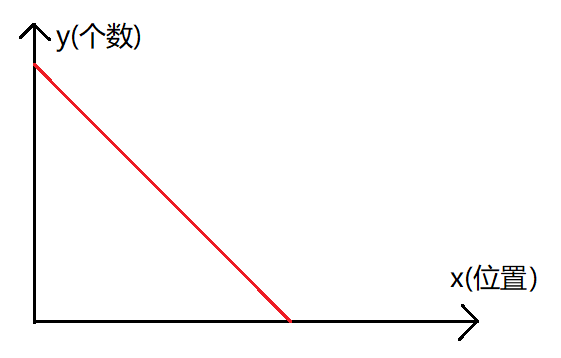
但是这样会有一个问题：某些区间会计算重复。

由于考虑的是这段该数出现位置的贡献，因此区间不能包含其它的该数，即贡献区间的最端点不能达到上一个出现位置。

因此可以得到如下的图：

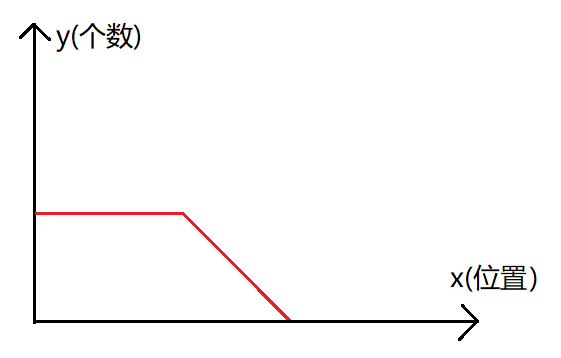
（好，以上只是理论部分...）

考虑一下我们需要做的：

我们枚举该数出现位置的右端点，并计算 [上一个出现的位置,当前位置) 区间的贡献。我们维护所有前面的这样的折线，统计所有折线在这段区间的面积和。

然后，由于多了当前位置，相当于以前的区间中选择区间的长度加了2，因此这些折线需要向右平移2个单位。

最后，需要把当前位置对应的折线维护起来。

一条折线可以看作是两条直线作差，因此我们需要做的有：添加直线、维护直线面积、支持直线集体向右平移。可以使用Treap来维护。

按照直线与x轴交点来维护，维护直线的斜率、截距、面积，以及子树中这三者的和。插入直接正常插入，整体平移则直接打标记。

统计面积的过程可以转化为前缀相减。在Treap上查询，如果其与左边的位置都小于当前位置，那么左边的答案就是面积总和，递归右子树；否则右边的贡献都是梯形面积（转化为等差数列求和），递归左子树。

然后就可以了，注意开long long。

细节贼多...

时间复杂度$O(n\log n)$

然后我考试时写的SBT，由于没有在旋转时pushdown（震惊！SBT竟然要在旋转时pushdown）导致爆0，再也不写SBT了...

附上Treap的代码：

#include <vector>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define N 500010
using namespace std;
typedef long long ll;
vector<int> v[N];
int l[N] , r[N] , rnd[N] , tot , root , a[N];
ll vp[N] , tag[N] , wk[N] , wb[N] , ws[N] , sk[N] , sb[N] , ss[N];
inline void add(int k , ll x)
{
	vp[k] += x;
	ws[k] += (2 * wb[k] - (x + 1) * wk[k]) * x / 2;
	ss[k] += (2 * sb[k] - (x + 1) * sk[k]) * x / 2;
	wb[k] -= wk[k] * x;
	sb[k] -= sk[k] * x;
	tag[k] += x;
}
inline void pushup(int k)
{
	sk[k] = sk[l[k]] + sk[r[k]] + wk[k];
	sb[k] = sb[l[k]] + sb[r[k]] + wb[k];
	ss[k] = ss[l[k]] + ss[r[k]] + ws[k];
}
inline void pushdown(int k)
{
	if(tag[k]) add(l[k] , tag[k]) , add(r[k] , tag[k]) , tag[k] = 0;
}
inline void zig(int &k)
{
	int t = l[k];
	l[k] = r[t] , r[t] = k , pushup(k) , pushup(t) , k = t;
}
inline void zag(int &k)
{
	int t = r[k];
	r[k] = l[t] , l[t] = k , pushup(k) , pushup(t) , k = t;
}
void insert(int &k , ll p , ll xk , ll xb)
{
	if(!k)
	{
		k = ++tot , vp[k] = p , wk[k] = sk[k] = xk , wb[k] = sb[k] = xb , ws[k] = ss[k] = xb * (p + 1) / 2 , rnd[k] = rand();
		return;
	}
	pushdown(k);
	if(p < vp[k])
	{
		insert(l[k] , p , xk , xb) , pushup(k);
		if(rnd[l[k]] < rnd[k]) zig(k);
	}
	else
	{
		insert(r[k] , p , xk , xb) , pushup(k);
		if(rnd[r[k]] < rnd[k]) zag(k);
	}
}
ll query(int k , ll p)
{
	if(!k) return 0;
	pushdown(k);
	if(p < vp[k]) return (2 * (wb[k] + sb[r[k]]) + (wk[k] + sk[r[k]]) * p) * (p + 1) / 2 + query(l[k] , p);
	else return ws[k] + ss[l[k]] + query(r[k] , p);
}
void clear(int k)
{
	if(!k) return;
	clear(l[k]) , clear(r[k]) , l[k] = r[k] = vp[k] = tag[k] = wk[k] = wb[k] = ws[k] = sk[k] = sb[k] = ss[k] = 0;
}
int main()
{
	int n , i , pos;
	ll ans = 0;
	unsigned j;
	scanf("%d%*d" , &n);
	for(i = 1 ; i <= n ; i ++ ) scanf("%d" , &a[i]) , v[++a[i]].push_back(i);
	for(i = 1 ; i <= n ; i ++ ) v[i].push_back(n + 1);
	for(i = 1 ; i <= n ; i ++ )
	{
		pos = 0;
		for(j = 0 ; j < v[i].size() ; j ++ )
		{
			ans += query(root , v[i][j] - 1) - query(root , pos - 1);
			add(root , 2);
			insert(root , v[i][j] + 1 , -1 , v[i][j] + 1) , insert(root , pos + 1 , 1 , -pos - 1);
			pos = v[i][j];
		}
		clear(root) , root = tot = 0;
	}
	printf("%lld\n" , ans);
	return 0;
}