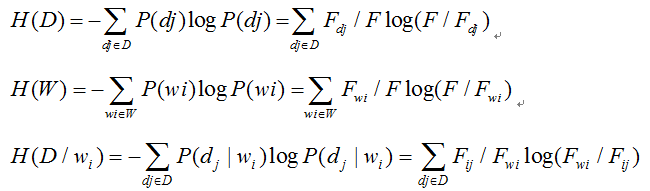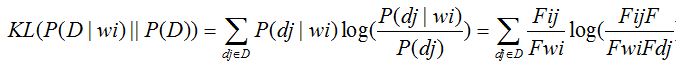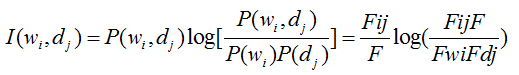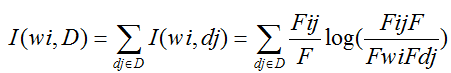从互信息的角度来理解tf-idf
先介绍tf idf
在一份给定的文件里,词频(term frequency,tf)指的是某一个给定的词语在该文件中出现的频率。这个数字是对词数(term count)的归一化,以防止它偏向长的文件。(同一个词语在长文件里可能会比短文件有更高的词数,而不管该词语重要与否。)对于在某一特定文件里的词语
以上式子中


逆向文件频率(inverse document frequency,idf)是一个词语普遍重要性的度量。某一特定词语的idf,可以由总文件数目除以包含该词语之文件的数目,再将得到的商取以10为底的对数得到:
其中
- |D|:语料库中的文件总数
:包含词语
的文件数目(即
的文件数目)如果词语不在数据中,就导致分母为零,因此一般情况下使用
然后
某一特定文件内的高词语频率,以及该词语在整个文件集合中的低文件频率,可以产生出高权重的tf-idf。因此,tf-idf倾向于过滤掉常见的词语,保留重要的词语。
互信息:
一般地,两个离散随机变量 X 和 Y 的互信息可以定义为:
其中 p(x,y) 是 X 和 Y 的联合概率分布函数,而

其中 p(x,y) 当前是 X 和 Y 的联合概率密度函数,而 

如果对数以 2 为基底,互信息的单位是bit。
直观上,互信息度量 X 和 Y 共享的信息:它度量知道这两个变量其中一个,对另一个不确定度减少的程度。例如,如果 X 和 Y 相互独立,则知道 X 不对 Y 提供任何信息,反之亦然,所以它们的互信息为零。在另一个极端,如果 X 是 Y 的一个确定性函数,且 Y 也是 X 的一个确定性函数,那么传递的所有信息被 X 和 Y共享:知道 X 决定 Y 的值,反之亦然。因此,在此情形互信息与 Y(或 X)单独包含的不确定度相同,称作 Y(或 X)的熵。而且,这个互信息与 X 的熵和 Y 的熵相同。(这种情形的一个非常特殊的情况是当 X 和 Y 为相同随机变量时。)
互信息是 X 和 Y 联合分布相对于假定 X 和 Y 独立情况下的联合分布之间的内在依赖性。 于是互信息以下面方式度量依赖性:I(X; Y) = 0 当且仅当 X 和 Y 为独立随机变量。从一个方向很容易看出:当 X 和 Y 独立时,p(x,y) = p(x) p(y),因此:
此外,互信息是非负的(即 I(X;Y) ≥ 0; 见下文),而且是对称的(即 I(X;Y) = I(Y;X))。
我们首先列出以下要用的一些变量:
D:文档随机变量D。
P(D):D的分布。
W:词条随机变量W。
P(W):W的分布。
P(D|W):已知W,D的条件分布。
P(wi,dj):提出词条wi,得到dj的概率。
F:所有文档相加的总次数。
Fij:词条i在文档j中出现的频率。
Fwi:词条wi在所有文档中的总频率。
Fdj:单个文档dj中的词数。
基于频率的概率模型:
我们假设词条wi提出的频率等于其出现的频率:
P(Wi)=Fwi/F
每个文档的出现概率与其包含词数成正比:
P(dj)=Fdj/F
提出wi以后,每个文档被取出的概率,也等于其包含wi频率比例:
P(dj|wi)=Fij/Fwi
Wi和dj同时发生的概率等于dj包含词条wi的频率:
P(wi,dj)=P(wi)*P(dj|wi)=Fwi/F*Fij/Fwi=Fij/F
H表示信息熵,I表示互信息,KL表示KL距离.
于是,再带入之前的信息论模型,得到:
熵:
KL距离:
PWI(互信息):
(1)
(2)
参考资料:
https://blog.csdn.net/ice110956/article/details/17243071
从互信息的角度来理解tf-idf的更多相关文章
- TF/IDF(term frequency/inverse document frequency)
TF/IDF(term frequency/inverse document frequency) 的概念被公认为信息检索中最重要的发明. 一. TF/IDF描述单个term与特定document的相 ...
- 文本分类学习(三) 特征权重(TF/IDF)和特征提取
上一篇中,主要说的就是词袋模型.回顾一下,在进行文本分类之前,我们需要把待分类文本先用词袋模型进行文本表示.首先是将训练集中的所有单词经过去停用词之后组合成一个词袋,或者叫做字典,实际上一个维度很大的 ...
- tf idf公式及sklearn中TfidfVectorizer
在文本挖掘预处理之向量化与Hash Trick中我们讲到在文本挖掘的预处理中,向量化之后一般都伴随着TF-IDF的处理,那么什么是TF-IDF,为什么一般我们要加这一步预处理呢?这里就对TF-IDF的 ...
- Elasticsearch由浅入深(十)搜索引擎:相关度评分 TF&IDF算法、doc value正排索引、解密query、fetch phrase原理、Bouncing Results问题、基于scoll技术滚动搜索大量数据
相关度评分 TF&IDF算法 Elasticsearch的相关度评分(relevance score)算法采用的是term frequency/inverse document frequen ...
- Android AsyncTask完全解析,带你从源码的角度彻底理解
转载请注明出处:http://blog.csdn.net/guolin_blog/article/details/11711405 我们都知道,Android UI是线程不安全的,如果想要在子线程里进 ...
- 从逆向的角度去理解C++虚函数表
很久没有写过文章了,自己一直是做C/C++开发的,我一直认为,作为一个C/C++程序员,如果能够好好学一下汇编和逆向分析,那么对于我们去理解C/C++将会有很大的帮助,因为程序中所有的奥秘都藏在汇编中 ...
- 基于TF/IDF的聚类算法原理
一.TF/IDF描述单个term与特定document的相关性TF(Term Frequency): 表示一个term与某个document的相关性. 公式为这个term在document中出 ...
- [转]Android事件分发机制完全解析,带你从源码的角度彻底理解(上)
Android事件分发机制 该篇文章出处:http://blog.csdn.net/guolin_blog/article/details/9097463 其实我一直准备写一篇关于Android事件分 ...
- 使用solr的函数查询,并获取tf*idf值
1. 使用函数df(field,keyword) 和idf(field,keyword). http://118.85.207.11:11100/solr/mobile/select?q={!func ...
随机推荐
- 高性能网站服务器的架设优化-Nginx优化
一:对于高性能网站 ,请求量大,如何支撑?思路 在网站架构设计中,大家一定对 LNMP (Linux Nginx Mysql Php) 不陌生.LNMP 确实是一个非常优秀的架构,秉承着自由,开放,高 ...
- 接口测试工具 — jmeter(关联)
1.正则表达式 1)添加正则表达式提取器 2)提取关联词 3)填写正则表达式 4)使用关联,其他请求使用${sign2}代替变量值 2. 1)添加提取器 2)填写变量值 3)使用关联,其他请求使用${ ...
- mysql数据库转移到oracle的经历
简单说明一下情况,系统原本是LAMP的.现在要添加对oracle的支持,原来的mysql也同样支持(通过配置选择数据库类型). 第一步,表结构转移到oracle,并掌握转移的方法(方便给有二开的老客户 ...
- FastReports_4.14.1 _Cliff手动安装
首次编译frx15.dproj包的时候,会出错: [DCC Fatal Error] fs15.dpk(59): F1026 File not found: 'fs_ipascal.dcu'原因是因为 ...
- .net ASPxGridView 使用手记
统计汇总功能: TotalSummary属性:此属性必须设置KeyFieldName属性:Settings中的ShowFooter属性设置为True. DisplayFormat:同.net中的Str ...
- SQL 将列转成字符串并用逗号分隔
SELECT STUFF((SELECT ',' + FieldName FROM TableName FOR XML PATH('')),1,1,'') AS T 其中的逗号可以换成其它字符 转换完 ...
- Pantone色卡——安全装备的面板、丝印及铭牌颜色设计参考
可以参考上传文件<Pantone色卡电子版下载>
- Android学习九---OpenCV4android org.opencv.feature2d
不管是在识别,配准等应用中,提取图像的特征都是很关键的一环,提取特征是先找出图像的关键点(如角点,边缘点等),然后用描述子来描述这些点,最后整幅图像就可以表示成一个特征向量,特征向量就可以利用在后续识 ...
- go——结构
Go语言中数组可以存储同一类型的数据,但在结构体中我们可以为不同项定义不同的数据类型.结构体是由一系列具有相同类型或不同类型的数据构成的数据集合. 结构体定义需要使用type和struct语句.str ...
- MySQL的搜索引擎,统一字符编码 和忘记MySQL密码如何破解
忘记mysql密码 linux平台下,破解密码的两种方式 [root@egon ~]# rm -rf /var/lib/mysql/mysql #所有授权信息全部丢失!!! [root@egon ~] ...