ID3、C4.5和CART决策树对比

ID3决策树：利用信息增益来划分节点

信息熵是度量样本集合纯度最常用的一种指标。假设样本集合D中第k类样本所占的比重为pk，那么信息熵的计算则为下面的计算方式

当这个Ent(D)的值越小，说明样本集合D的纯度就越高

有了信息熵，当我选择用样本的某一个属性a来划分样本集合D时，就可以得出用属性a对样本D进行划分所带来的“信息增益”

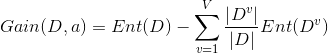
一般来讲，信息增益越大，说明如果用属性a来划分样本集合D，那么纯度会提升，因为我们分别对样本的所有属性计算增益情况，选择最大的来作为决策树的一个结点，或者可以说那些信息增益大的属性往往离根结点越近，因为我们会优先用能区分度大的也就是信息增益大的属性来进行划分。当一个属性已经作为划分的依据，在下面就不在参与竞选了，我们刚才说过根结点代表全部样本，而经过根结点下面属性各个取值后样本又可以按照相应属性值进行划分，并且在当前的样本下利用剩下的属性再次计算信息增益来进一步选择划分的结点，ID3决策树就是这样建立起来的。

C4.5决策树：先算信息增益，然后再选取增益率最高的

C4.5决策树的提出完全是为了解决ID3决策树的一个缺点，当一个属性的可取值数目较多时，那么可能在这个属性对应的可取值下的样本只有一个或者是很少个，那么这个时候它的信息增益是非常高的，这个时候纯度很高，ID3决策树会认为这个属性很适合划分，但是较多取值的属性来进行划分带来的问题是它的泛化能力比较弱，不能够对新样本进行有效的预测。

而C4.5决策树则不直接使用信息增益来作为划分样本的主要依据，而提出了另外一个概念，增益率

但是同样的这个增益率对可取值数目较少的属性有所偏好，因此C4.5决策树先从候选划分属性中找出信息增益高于平均水平的属性，在从中选择增益率最高的。

CART决策树：

CART决策树的全称为Classification and Regression Tree,可以应用于分类和回归。

采用基尼系数来划分属性

基尼值：

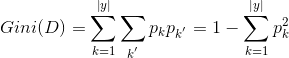
基尼系数：

分类：输出的是一个类别

回归：输出的是一个值，这个值在构建的过程中，就已经计算好了

分类：可以选择GINI，双化或有序双化

回归：可以使用最小二乘偏差（LSD）或最小绝对偏差（LAD）