笛卡尔树Cartesian Tree

前言

最近做题目，已经不止一次用到笛卡尔树了。这种数据结构极为优秀，但是构造的细节很容易出错。因此写一篇文章做一个总结。

笛卡尔树 Cartesian Tree

引入问题

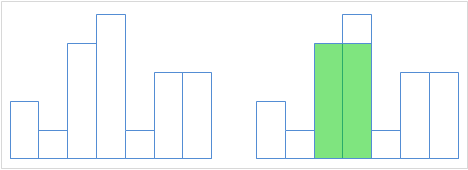
有N条的长条状的矩形，宽度都为1，第i条高度为H_i，相邻的竖立在x轴上，求最大的子矩形面积。

约定

1 ≤ N ≤ 10⁵

1 ≤ H_i ≤ 10⁹

分析

我们只需要求出每条矩形最多可以向两边拓展的宽度，就可以算出以这个矩形高度为高的最大子矩形面积。最后我们求一个最大值即可。

下面我们还是回到之前的笛卡尔树。

概念

笛卡尔树的树根是这一子树中键值最小（或最大）的元素；且对于某个序列的笛卡尔树，其任一子树的中序遍历恰好是对应了原序列中的一段连续区间。

性质

我们会发现笛卡尔树同时满足二叉树搜索和堆的性质：

1. 中序遍历即为原数组序列
2. 父节点的键值均小于（或大于）其左右子节点的键值

构造

我们可以利用单调栈在线性时间内对给定的数组序列构造出其笛卡尔树。

首先，由于笛卡尔树的中序遍历为原数组序列，那么我们设

T_i为当前序列中[1..i]区间的笛卡尔树，

那么，一定有：

第(i+1)个节点属于T_i最右边的那一条路径。

那么对于有已经构造好的T_i和第(i+1)个节点，我们只需要沿着T_i最右边的路径从下往上找，直到发现当前节点可以放的位置。

我们可以用一个单调栈来维护最右边的这条路径，当前根节点压在栈底，对于当前节点，我们将它与栈顶比较，若栈顶不能做它的父节点，则将栈顶弹出。

由于每个点进栈和出栈至多一次，因此这个构造的复杂度为O(n)的。

参考代码

节点用结构体定义

（这里我们用指针会方便许多）

struct Node {
    int index, val;    // index表示原数组的索引，val为当前节点的键值
    Node *parent, *lefts, *rights;    // 这三个指针分别指向父节点，左子节点，右子节点
    Node(int id = , int v = , Node *l = NULL, Node *r = NULL) { index = id; val = v; lefts = l; rights = r; }
};

树构造函数

（这里要注意的细节较多）

Node * build(int arr[], int size) {    // 这里构建一个根节点为最小值的笛卡尔树
    std::stack<Node * > S;    // 存储最右边路径的栈
    Node *now, *next, *last;
    for (int i = ; i < size; i++) {
        next = new Node(i, arr[i]); last = NULL;    // last用来指向最后被弹出栈的元素（若有弹出），它的作用后面会写到
        while (!S.empty()) {
            if (S.top()->val < next->val) {    // 若栈顶节点的键值比当前节点键值小了，那么当前节点就做栈顶节点的右子节点
                now = S.top();
                if (now->rights) {    // 而栈顶节点的原右子节点要变成当前节点的左子节点（由于前面一定与当前节点比较过了，栈顶节点右子树的键值一定都比当前节点大）
                    now->rights->parent = next;
                    next->lefts = now->rights;
                }
                now->rights = next;
                next->parent = now;
                break;
            }
            last = S.top();
            S.pop();
        }
        if (S.empty() && last) {    // 这里为了特判一种可能出现的情况，就是当前节点把栈全部弹空了，就要把原先的根节点作为当前节点的左子节点
            next->lefts = last;
            last->parent = next;
        }
        S.push(next);
    }
    while (!S.empty()) now = S.top(), S.pop();
    return now;
}