[leetcode]238. Product of Array Except Self除了自身以外的数组元素乘积

Given an array nums of n integers where n > 1,  return an array output such that output[i] is equal to the product of all the elements of nums except nums[i].

Example:

Input:  [1,2,3,4]
Output: [24,12,8,6]

Note: Please solve it without division and in O(n).

思路

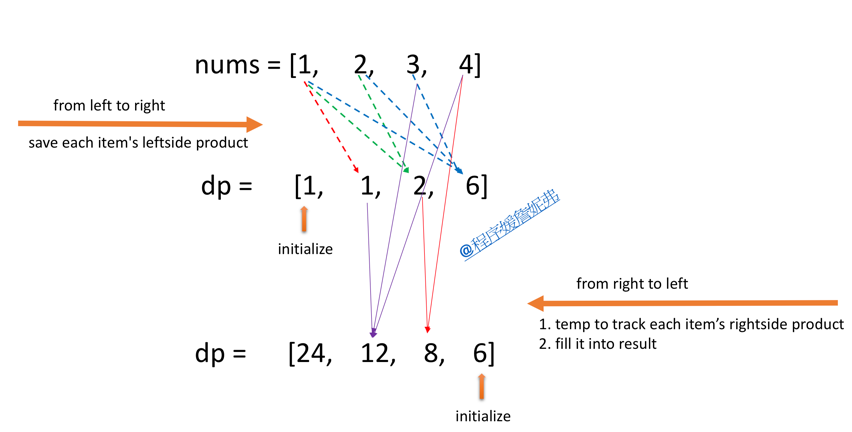
1. from left to right,  save each item's left side product

2. from right to left, maintain a variable temp to track each item's right side product, then fill product (left * right) into result

代码

 class Solution {
     public int[] productExceptSelf(int[] nums) {
         int[]dp = new int[nums.length];

         dp[0] = 1;

         // left to right
         for( int i = 1; i< nums.length; i++){
             dp[i] = dp[i-1] * nums[i-1];
         }
         // right to left
         int temp = 1;
         for( int i = nums.length-1; i>=0; i--){
             dp[i] = dp[i] *temp;
             temp = temp*nums[i];
         }
         return dp;

     }
 }