KMP(2)

KMP 算法（2）：其细微之处

• 2017 年 05 月 13 日
• • 技术

系列文章目录

KMP 算法（1）：如何理解 KMP
KMP 算法（2）：其细微之处

本篇来谈一谈 KMP 的一些细微之处，直接进入主题。

一：起始下标之 “争”：0 和 1展开目录

/* P 为模式串，下标从 0 开始 */
void GetNext(string P, int next[])
{
    int p_len = P.size();
    int i = 0;   // P 的下标
    int j = -1;  // 相同真前后缀的长度
    next[0] = -1;

    while (i < p_len)
    {
        if (j == -1 || P[i] == P[j])
        {
            i++;
            j++;
            next[i] = j;
        }
        else
            j = next[j];
    }
}

/* 在 S 中找到 P 第一次出现的位置 */
int KMP(string S, string P, int next[])
{
    GetNext(P, next);

    int i = 0;  // S 的下标
    int j = 0;  // P 的下标
    int s_len = S.size();
    int p_len = P.size();

    while (i < s_len && j < p_len)
    {
        if (j == -1 || S[i] == P[j])  // P 的第一个字符不匹配或 S[i] == P[j]
        {
            i++;
            j++;
        }
        else
            j = next[j];  // 当前字符匹配失败，进行跳转
    }

    if (j == p_len)  // 匹配成功
        return i - j;

    return -1;
}

上述代码的起始下标都是从 0 开始的，但每个人对数组起始位置的编码习惯不同，分为两类：0 和 1。对于上面的代码，起始位置如果改为 1 的话又是怎样呢？

 

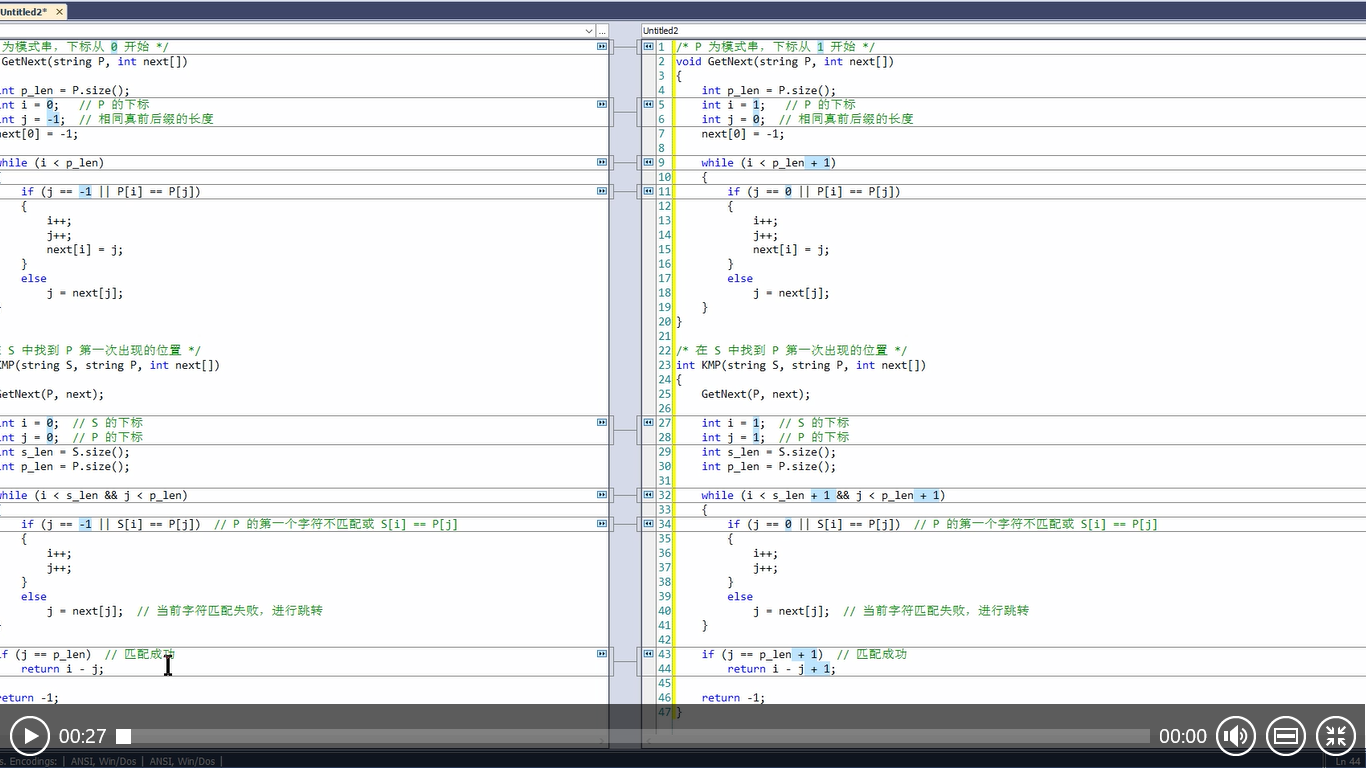
但它们的区别并不止如此。我们知道，KMP 算法的 next[i] 表示最长的相同真前后缀，但这对起始位置为 1 的 next[i] 却不再适用。

i	0	1	2	3	4	5	6	7
模式串	A	B	C	D	A	B	D	'\0'
next[i]	-1	0	0	0	0	1	2	0

i	1	2	3	4	5	6	7	8
模式串	A	B	C	D	A	B	D	'\0'
next[i]	0	1	1	1	1	2	3	1

上面两个表格表展示的是：相同模式串下不同起始位置的 next 值对比。

相比之下，起始位置为 1 的 next 值比起始位置为 0 的 next 值多了 1。多 1，不是巧合，而是必然。这很容易证明。

在 GetNext() 中，j 从 0 开始（起始位置为 1），在走了相等步后停下依次赋值给 next[i]，因此相较于起始位置为 0 的 next 总是多 1。这又引起了我们的思考，多了 1 后在模式匹配中，next 还会正确的实现跳转么？当然会了，next 多 1，同时模式串的起始位置也多了 1，这就好比数学中，从 a=b 转化为 a+1=b+1，形式不同但完全等价。

二：next[i] 里最不起眼处的妙用展开目录

先来看一个问题，在主串 S 中找到模式串 P 所有可以完全匹配的位置。

很简单，典型的 KMP 模式匹配。

假设起始位置都是从 0 开始，对于上图，若已找到主串的第一个完全匹配位置即 0--4，那么请问接下来模式串如何移动？

不知道各位读者有没有注意过模式串最后末尾处的 next 值代表什么？（末尾即为字符串的结尾标志：'\0'）

它代表整个模式串的最长相同真前后缀。

利用这个 next 值，我们直接可以实现跳转，更快地找到下一个匹配点。