堆 Heap

2018-03-01 20:38:34

堆（Heap）是可以用来实现优先的队列的数据结构，而不是堆栈。

• 若采用数组或者链表实现优先队列

• 若采用树的结构

如果采用二叉搜索树，那么每次删除，比如删除最大值，也就是删除最右边的叶子，那么很快这棵二叉树就不再平衡了。

那能否采用别的方法来构造树呢？

我们可以这样构造二叉树：每课树最大的元素在根处，且该定义是递归的，另外，为了保证效率，这棵树还应该是完全二叉树。

其实这就是堆的定义。

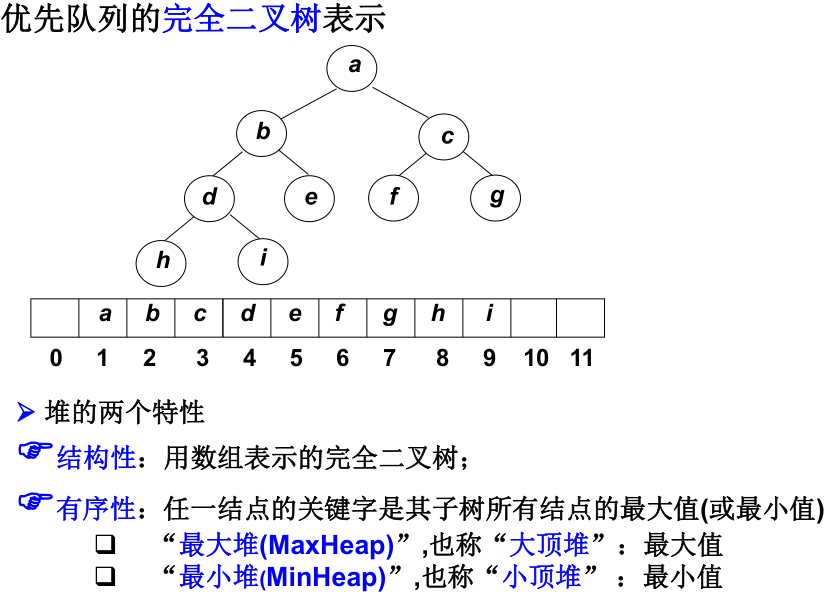
堆的抽象数据类型描述：

1）最大堆的初始化

2）堆的插入

算法描述：将插入元素放到末尾，并进行调整，将之最终插入从其父结点到根结点的有序序列中去。

时间复杂度：O（logn）

3）堆的删除

算法描述：显然为了维护完全二叉树的特点，删除的元素在末尾是比较合适的。最大堆的定义指出删除应该是删除最大值，也就是删除根结点。此时，可以采用将根结点与末尾的结点数值替换的方法，来间接的删除最大值。在末尾值移到根部之后可能会打破堆的定义，此时需要进行堆的维护。

时间复杂度：O（logn）

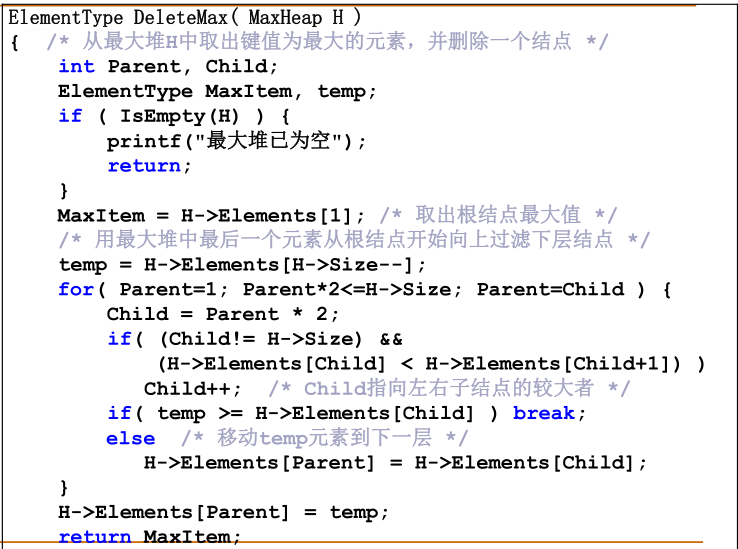
4）最大堆的建立

既然已经有了插入的算法，当然可以逐个进行插入，基于这种的算法的时间复杂是O（nlog（n））。

事实上，可以在O（n）的时间复杂度内完成建立堆，具体的思路就是首先由数组已经建立了一个完全二叉树，这时候，自底向上进行维护，这样做的目的是为了满足堆维护算法的合法性：堆的左右子树都是堆。这种算法的时间复杂度为O（n）。