相机IMU融合四部曲(二):误差状态四元数详细解读
相机IMU融合四部曲(二):误差状态四元数详细解读
极品巧克力
前言
上一篇文章,《D-LG-EKF详细解读》中,讲了理论上的SE3上相机和IMU融合的思想。但是,还没有涉及到实际的操作,以及实际操作中会遇到的一些问题。所以,本文开始讲实际操作,包括,在相机和IMU融合的过程中,IMU速度的计算,加速度计和陀螺仪的使用,偏移的处理,重力的滤波等。
本文的主要参考文献为John sola的《Quaternion kinematics for the error state Kalman》,简称为误差状态四元数。它的基本思想和D-LG-EKF是一样的,都是对均值状态和扰动状态的进行处理。但是,不同的是,在误差状态四元数里,是把偏移也放到状态里滤波的,而Google Cardboard里的偏移是通过低通滤波滤出来的。
而且John sola的相机和IMU融合的程序是开源的,项目名称为RT-SLAM,源代码地址为https://www.openrobots.org/wiki/rtslam/。
其运行效果如视频(https://vimeo.com/114879173)所示。
本文目标读者:传感器融合算法工程师。
1.预测
首先,列出运动方程。

其中,下标t表示的是true的意思。
又因为实际测量值与真实值的关系为,
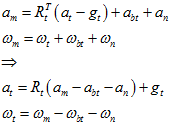
把实际测量值代入到上式中,
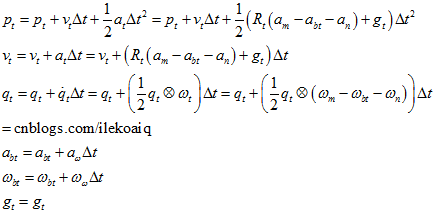
所以,用D-LG-EKF里面的均值+扰动的思想,表示两个时刻的均值以及扰动状态之间要满足的关系,
因为,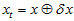 ,所以,代入上式,得到,
,所以,代入上式,得到,
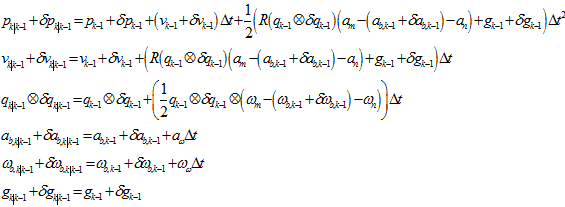
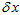 里面,其实是
里面,其实是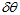 ,而不是
,而不是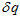 ,
,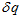 是中间的一个转换。
是中间的一个转换。
其中,上式左边的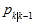 等都为均值,就是由
等都为均值,就是由 时刻的均值变换过来的,新的均值的计算过程如下,
时刻的均值变换过来的,新的均值的计算过程如下,
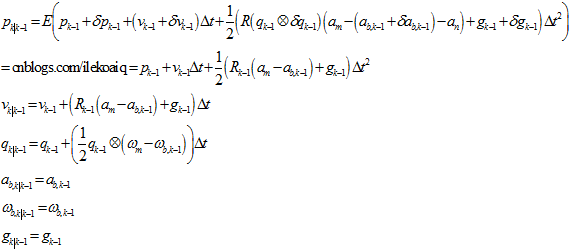
再代回到之前的公式中,
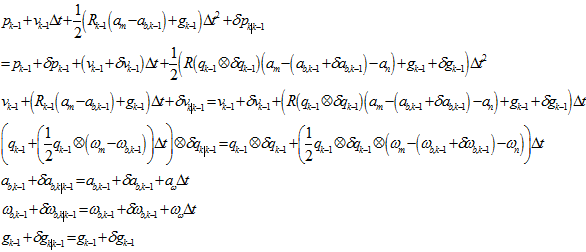
从而得到,新的扰动与旧的扰动的关系,

把 的平方项都忽略掉,忽略二阶的极小值,进一步推导。
的平方项都忽略掉,忽略二阶的极小值,进一步推导。
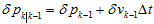
参考《从角轴到四元数微分方程》,角轴扰动与四元数扰动的关系为,
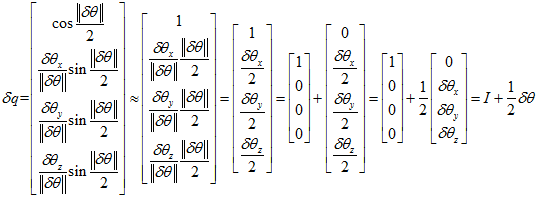
原先的表达式可以转换为,

在上面的推导中,因为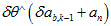 是二阶极小值,所以忽略掉。因为
是二阶极小值,所以忽略掉。因为 是各向相同的噪声,所以
是各向相同的噪声,所以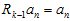 ,参考论文里面的推导,
,参考论文里面的推导,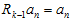 并不会影响协方差的计算。
并不会影响协方差的计算。
对下一个表达式进行转换,
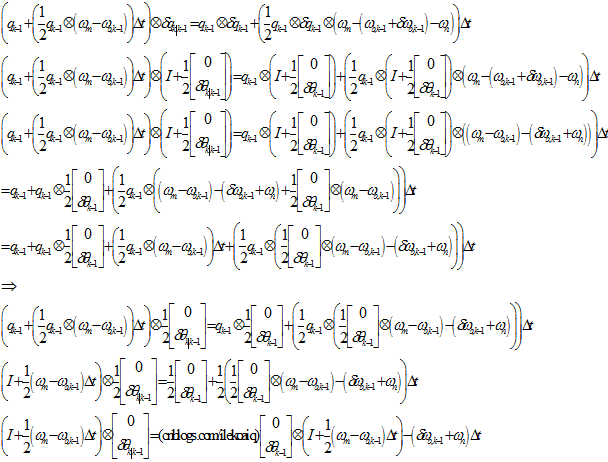
把上面的四元数乘法,全部都解开,应该就能算出来。但是太麻烦了。
利用,

上式转换为,

在上式中,因为,认为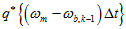 是一个微小值,所以直接
是一个微小值,所以直接 。
。
或者,另外一种方法,参考论文上的方法,对表达式两边求导,导数也应该是相同的。
因为, ,所以,
,所以,
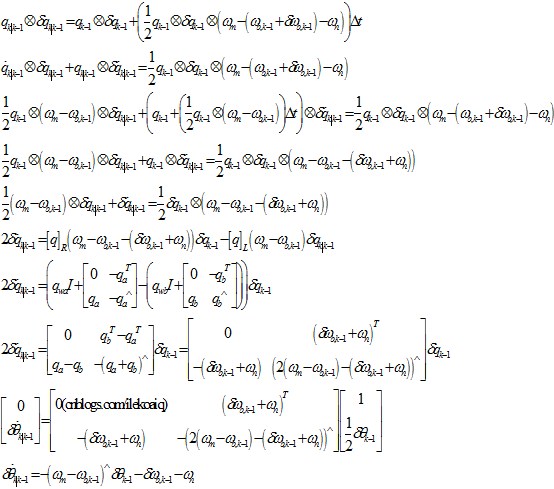
在上面,进行了两处简化,首先,忽略掉了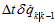 项,然后,
项,然后, 。积分之后,就得到,
。积分之后,就得到,

与前面那种方法的结果相同。但是,论文上的这种方法难想到,为了思考上的方便,以后仍然还是用前面的那种方法。
启发:这里用旋转矩阵,而不是叉乘,这么操作的目的应该是,叉乘只是对旋转矩阵的近似,而角轴转旋转矩阵,用罗德里格斯变换,得到的结果最准确。所以,最终结果里,还是尽量少用叉乘,能组合成旋转矩阵就组合成旋转矩阵,而角轴到旋转矩阵的方法用罗德里格斯变换。
然后,算后面的扰动。
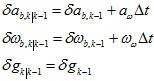
新的扰动与旧的扰动的关系,总结起来就是,

所以,都转换成了线性的关系,可以表示为,
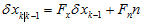
其中,

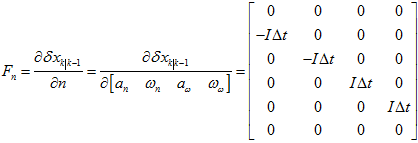
因为,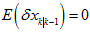 ,所以,
,所以,
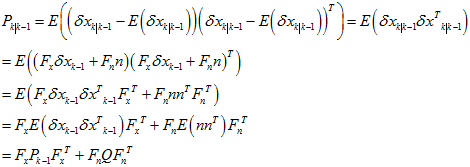
其中, 的计算,参考论文上的公式(270)。
的计算,参考论文上的公式(270)。

2.更新
然后,使用贝叶斯公式,用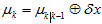 表示,
表示,
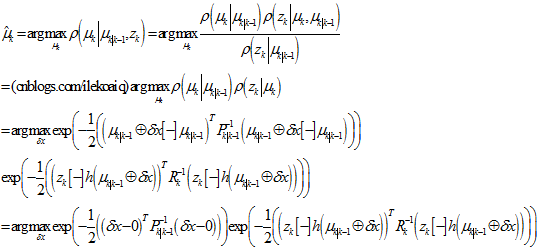
上面的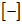 表示的是一种特殊的运算,意思是距离。
表示的是一种特殊的运算,意思是距离。
为了能像《D-LG-EKF》里面那样转换成卡尔曼滤波的形式,上式的右边内容,需要进行线性化。在扰动的均值处进行线性化,在这里,即为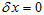 处进行线性化。
处进行线性化。
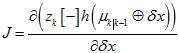
当然,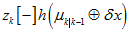 ,也可以进一步变换,比如,MSF里,把四元数残差转换成角轴残差。但这些残差都要有相对应的
,也可以进一步变换,比如,MSF里,把四元数残差转换成角轴残差。但这些残差都要有相对应的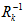 。
。
而在误差状态四元数论文里,是通过级联求导的方法。
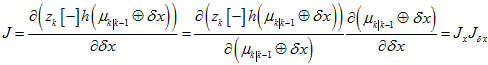
其中, 要根据具体的残差方程来计算,而
要根据具体的残差方程来计算,而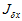 则是固定的。无论是四元数残差还是角轴残差,还是其它的残差,不同的仅仅只是
则是固定的。无论是四元数残差还是角轴残差,还是其它的残差,不同的仅仅只是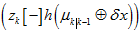 ,而
,而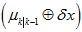 和
和 都是一样的。所以,上面的表达式,是一个通用模型,适用于所有的残差,也可以说是,适用于所有的观测。
都是一样的。所以,上面的表达式,是一个通用模型,适用于所有的残差,也可以说是,适用于所有的观测。
所以,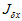 可以提前计算好,
可以提前计算好,
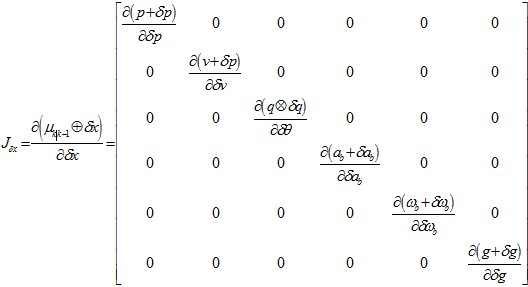
其中,其它项都是单位阵,除了 ,则计算如下,
,则计算如下,
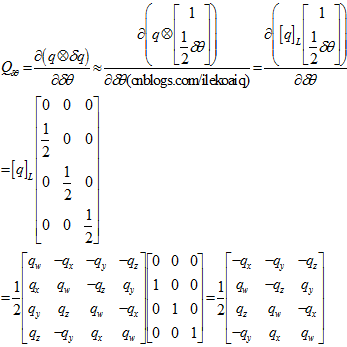
所以,
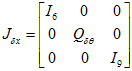
这是可以提前计算好的,在实际计算时,只需要把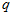 代进来就行。
代进来就行。
用 ,则原式可以转换为,
,则原式可以转换为,
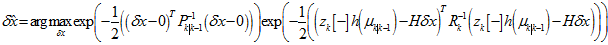
然后,就可以转换为卡尔曼滤波公式,这些对应的是扰动的均值和协方差,
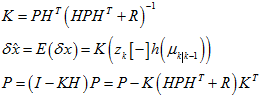
然后,就是把卡尔曼滤波算出来的最大后验值,加入到原先的状态中,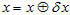 。
。
也就是论文里面的reset部分,就是让旧的状态吸收进卡尔曼滤波出来的扰动的均值,让新扰动的均值变为0。
则新的扰动,与旧的扰动的关系为,

其中,

代回到之前的公式,得到,
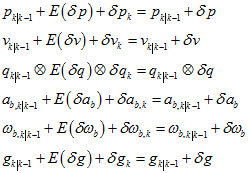
从而得到,
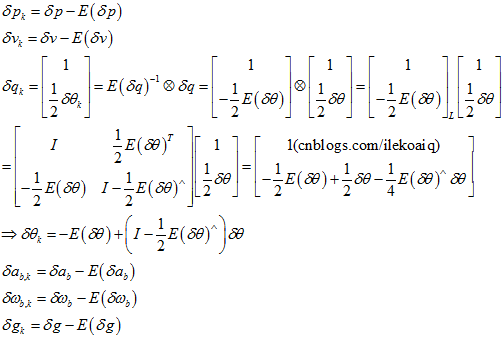
所以,新的扰动的均值为,
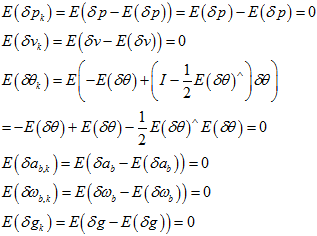
新的扰动的协方差为,
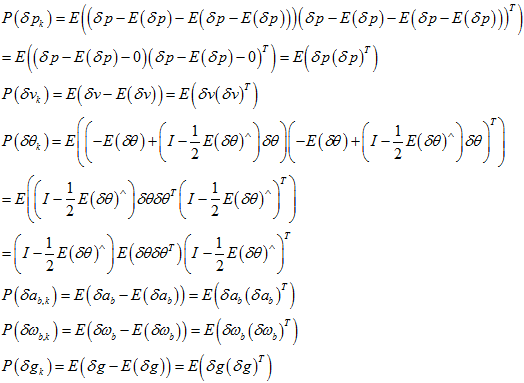
所以,也就得到的新的协方差,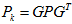 。
。
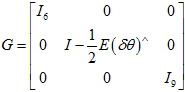
或者,也没必要这么麻烦,直接根据前面新旧扰动的关系,算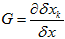 ,然后
,然后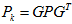 。其实根据协方差计算公式,本质上是一样的。
。其实根据协方差计算公式,本质上是一样的。
3.全局扰动
之前的扰动都是加在右边的,全局扰动就是加在左边的扰动。
全局扰动与本地扰动的区别,如论文中的表格4所示。差别不大,主要是角度上的扰动的雅克比。这里也计算一下。
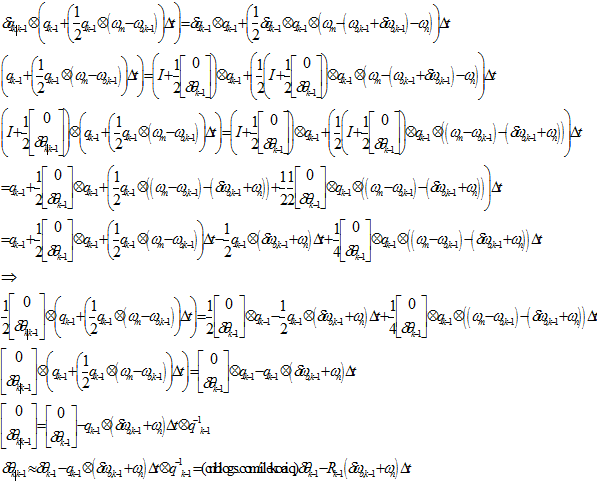
4.微分方程的积分
论文的附录部分,就是讨论用龙格库塔的方法,或者泰勒多阶展开的方法,对状态转移矩阵进行积分。
5.总结
虽然论文中有说这么一句话,全局扰动的方法比局部扰动的方法要好,比如李名杨的MSCKF中的方法,但是没有具体举例说明好在哪里。
用四元数来表示状态,四元数扰动与角轴扰动的转换太麻烦了,可以改成用李代数来表示旋转,但是李代数里面的BCH近似的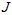 又不好算。
又不好算。
6.参考文献
- Solà J. Quaternion kinematics for the error-state Kalman filter[J]. 2017.
相机IMU融合四部曲(二):误差状态四元数详细解读的更多相关文章
- 相机IMU融合四部曲(三):MSF详细解读与使用
相机IMU融合四部曲(三):MSF详细解读与使用 极品巧克力 前言 通过前两篇文章,<D-LG-EKF详细解读>和<误差状态四元数详细解读>,已经把相机和IMU融合的理论全部都 ...
- 相机IMU融合四部曲(一):D-LG-EKF详细解读
相机IMU融合四部曲(一):D-LG-EKF详细解读 极品巧克力 前言 前两篇文章<Google Cardbord的九轴融合算法>,<Madgwick算法详细解读>,讨论的都是 ...
- 【用户状态】详细解读Oracle用户ACCOUNT_STATUS的九种状态
转至:http://blog.itpub.net/519536/viewspace-672276/ DBA_USERS视图中ACCOUNT_STATUS记录的用户的当前状态,一般情况下在使用的正常用户 ...
- 一步一步学习S-MSCKF(一)连续时间IMU误差状态运动模型
1 IMU真实状态运动模型 状态向量: \(x_{I}=\left[{{_{G}^{I}{q(t)}}^{T},{b_{g}(t)}^{T},{^{G}v_{I}(t)}^{T},{b_{a}(t)} ...
- VINS(四)初始化与相机IMU外参标定
和单目纯视觉的初始化只需要获取R,t和feature的深度不同,VIO的初始化话通常需要标定出所有的关键参数,包括速度,重力方向,feature深度,以及相机IMU外参$R_{c}^{b}$和$p_{ ...
- 相机-imu外参校准总结
1. 研究背景及相关工作 1)研究背景 单目视觉惯性slam是一种旨在跟踪移动平台的增量运动并使用来自单个车载摄像头和imu传感器的测量结果同时构建周围环境地图的技术.视觉相机和惯性测量单元(imu) ...
- 相机imu外参标定
1. 第一步初始化imu外参(可以从参数文档中读取,也可以计算出),VINS中处理如下: # Extrinsic parameter between IMU and Camera. estimate_ ...
- Introduction to 3D Game Programming with DirectX 12 学习笔记之 --- 第二十二章:四元数(QUATERNIONS)
原文:Introduction to 3D Game Programming with DirectX 12 学习笔记之 --- 第二十二章:四元数(QUATERNIONS) 学习目标 回顾复数,以及 ...
- 第2章 rsync(二):inotify+rsync详细说明和sersync
本文目录: inotify+rsync 1.1 安装inotify-tools 1.2 inotifywait命令以及事件分析 1.3 inotify应该装在哪里 1.4 inotify+rsync示 ...
随机推荐
- laravel的phpstorm插件laravel-ide-helper
地址https://github.com/barryvdh/laravel-ide-helper 简单记录下安装过程 项目目录下 composer require barryvdh/laravel-i ...
- cf Double Happiness(判断是否为素数且为4k+1型)
2790. Double Happiness time limit per test 3 seconds memory limit per test 128 megabytes input sta ...
- Java中split的用法
Java中的我们可以利用split把字符串按照指定的分割符进行分割,然后返回字符串数组,下面是string.split的用法实例及注意事项:java.lang.string.splitsplit 方法 ...
- java web 程序---刷新页面次数
<%! int count=0; %> <% count++; session.setAttribute("count",count); out.print(&q ...
- java web 程序---猜数字游戏
思路:1.第一个是随机产生的数字,告诉我们去猜 cai.jsp 2.第二个是一个form表单,提交按钮后,将连接到验证页面 test1.jsp 3.第三个是比较猜的数和随机数.对了,提示再玩一次,不 ...
- Java 静态对象 static
什么是静态变量 大家都知道,我们可以基于一个类创建多个该类的对象,每个对象都拥有自己的成员,互相独立. 然而在某些时候,我们更希望该类所有的对象共享同一个成员.此时就是 static 大显身手的时候了 ...
- 杂项-数学软件:MATLAB
ylbtech-杂项-数学软件:MATLAB MATLAB是美国MathWorks公司出品的商业数学软件,用于算法开发.数据可视化.数据分析以及数值计算的高级技术计算语言和交互式环境,主要包括MATL ...
- Jquery 页面初始化常用的三种方法以及Jquery 发送ajax 请求
第一种 $(document).ready(function(){ //文档就绪事件 }); 第二种是第一种的简略写法,效果上和第一种是等效的. $(function(){ //文档加载事件,整个文档 ...
- CentOS7.6安装Maven
官网下载地址:http://maven.apache.org/download.cgi 第一步:软件下载安装 进行安装目录:cd /opt/software (如果目录不存在,请先创建目录) 下载二进 ...
- 第四篇 Flask 中的模板语言 Jinja2 及 render_template 的深度用法
是时候开始写个前端了,Flask中默认的模板语言是Jinja2 现在我们来一步一步的学习一下 Jinja2 捎带手把 render_template 中留下的疑问解决一下 首先我们要在后端定义几个字符 ...
