python实现一个层次聚类方法

层次聚类(Hierarchical Clustering)

一.概念

　　层次聚类不需要指定聚类的数目，首先它是将数据中的每个实例看作一个类，然后将最相似的两个类合并，该过程迭代计算只到剩下一个类为止，类由两个子类构成，每个子类又由更小的两个子类构成。如下图所示：

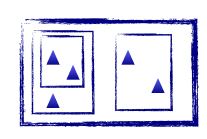
二.合并方法

在聚类中每次迭代都将两个最近的类进行合并，这个类间的距离计算方法常用的有三种：

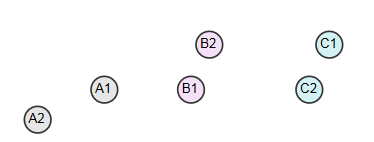
1.单连接聚类(Single-linkage clustering)

　　在单连接聚类中，两个类间的距离定义为一个类的所有实例到另一个类的所有实例之间最短的那个距离。如上图中类A(A1,A2)，B(B1,B2)，C(C1,C2)，A类和B类间的最短距离是A1到B1，所以A类与B类更近，所有A和B合并。

2.全连接聚类(Complete-linkage clustering)

　　在全连接聚类中，两个类间的距离定义为一个类的所有实例到另一个类的所有实例之间最长的那个距离。图中A类和B类间最长距离是A2到B2，B类和C类最长距离是B1到C1，distance(B1-C1)<distance(A2-B2)，所以B类和C类合并在一起。

3.平均连接聚类(Average-linkage clustering)

　　在平均连接聚类中，类间的距离为一个类的所有实例到另一个类的所有实例的平均距离。

三.python实现(单连接)

 #!/usr/bin/python
 # -*- coding: utf-8 -*-

 from queue import PriorityQueue
 import math
 import codecs

 """
 层次聚类
 """
 class HCluster:

     #一列的中位数
     def getMedian(self,alist):
         tmp = list(alist)
         tmp.sort()
         alen = len(tmp)
         if alen % 2 == 1:
             return tmp[alen // 2]
         else:
             return (tmp[alen // 2] + tmp[(alen // 2) - 1]) / 2

     #对数值型数据进行归一化，使用绝对标准分[绝对标准差->asd=sum(x-u)/len(x),x的标准分->(x-u)/绝对标准差，u是中位数]
     def normalize(self,column):
         median = self.getMedian(column)
         asd = sum([abs(x - median) for x in column]) / len(column)
         result = [(x - median) / asd for x in column]
         return result

     def __init__(self,filepath):
         self.data={}
         self.counter=0
         self.queue=PriorityQueue()
         line_1=True#开头第一行
         with codecs.open(filepath,'r','utf-8') as f:
             for line in f:
                 #第一行为描述信息
                 if line_1:
                     line_1=False
                     header=line.split(',')
                     self.cols=len(header)
                     self.data=[[] for i in range(self.cols)]
                 else:
                     instances=line.split(',')
                     toggle=0
                     for instance in range(self.cols):
                         if toggle==0:
                             self.data[instance].append(instances[instance])
                             toggle=1
                         else:
                             self.data[instance].append(float(instances[instance]))
         #归一化数值列
         for i in range(1,self.cols):
             self.data[i]=self.normalize(self.data[i])

         #欧氏距离计算元素i到所有其它元素的距离，放到邻居字典中，比如i=1,j=2...，结构如i=1的邻居-》{2: ((1,2), 1.23),  3: ((1, 3), 2.3)... }
         #找到最近邻
         #基于最近邻将元素放到优先队列中
         #data[0]放的是label标签，data[1]和data[2]是数值型属性
         rows=len(self.data[0])
         for i in range(rows):
             minDistance=10000
             nearestNeighbor=0
             neighbors={}
             for j in range(rows):
                 if i!=j:
                     dist=self.distance(i,j)
                     if i<j:
                         pair=(i,j)
                     else:
                         pair=(j,i)
                     neighbors[j]=(pair,dist)
                     if dist<minDistance:
                         minDistance=dist
                         nearestNeighbor=j
             #创建最近邻对
             if i<nearestNeighbor:
                 nearestPair=(i,nearestNeighbor)
             else:
                 nearestPair=(nearestNeighbor,i)
             #放入优先对列中，(最近邻距离，counter,[label标签名，最近邻元组，所有邻居])
             self.queue.put((minDistance,self.counter,[[self.data[0][i]],nearestPair,neighbors]))
             self.counter+=1

     #欧氏距离,d(x,y)=math.sqrt(sum((x-y)*(x-y)))
     def distance(self,i,j):
         sumSquares=0
         for k in range(1,self.cols):
             sumSquares+=(self.data[k][i]-self.data[k][j])**2
         return math.sqrt(sumSquares)

     #聚类
     def cluster(self):
         done=False
         while not done:
             topOne=self.queue.get()
             nearestPair=topOne[2][1]
             if not self.queue.empty():
                 nextOne=self.queue.get()
                 nearPair=nextOne[2][1]
                 tmp=[]
                 #nextOne是否是topOne的最近邻，如不是继续找
                 while nearPair!=nearestPair:
                     tmp.append((nextOne[0],self.counter,nextOne[2]))
                     self.counter+=1
                     nextOne=self.queue.get()
                     nearPair=nextOne[2][1]
                 #重新加回Pop出的不相等最近邻的元素
                 for item in tmp:
                     self.queue.put(item)

                 if len(topOne[2][0])==1:
                     item1=topOne[2][0][0]
                 else:
                     item1=topOne[2][0]
                 if len(nextOne[2][0])==1:
                     item2=nextOne[2][0][0]
                 else:
                     item2=nextOne[2][0]
                 #联合两个最近邻族成一个新族
                 curCluster=(item1,item2)
                 #下面使用单连接方法建立新族中的邻居距离元素，一：计算上面新族的最近邻。二：建立新的邻居。如果 item1和item3距离是2，item2和item3距离是4，则在新族中的距离是2
                 minDistance=10000
                 nearestPair=()
                 nearestNeighbor=''
                 merged={}
                 nNeighbors=nextOne[2][2]
                 for key,value in topOne[2][2].items():
                     if key in nNeighbors:
                         if nNeighbors[key][1]<value[1]:
                             dist=nNeighbors[key]
                         else:
                             dist=value
                         if dist[1]<minDistance:
                             minDistance=dist[1]
                             nearestPair=dist[0]
                             nearestNeighbor=key
                         merged[key]=dist
                 if merged=={}:
                     return curCluster
                 else:
                     self.queue.put((minDistance,self.counter,[curCluster,nearestPair,merged]))
                     self.counter+=1

 if __name__=='__main__':
     hcluser=HCluster('filePath')
     cluser=hcluser.cluster()
     print(cluser)

参考：1.machine.learning.an.algorithmic.perspective.2nd.edition.

　　　 2.a programmer's guide to data mining