NOIP 2010 P1514 引水入城

题目：传送门

题目概要：有一个n行m列的矩阵，每一个格子都有一个高度，路径只能从高处向低处扩散，问你如果最后一行可以全部被覆盖，最少要从第一行多少个格子开始，如果不能使最后一行全部被覆盖，求有多少个格子不能；

看完这道题，最直接的想法就是直接定义dx,dy两个数组表示上下左右走，看看第一行每一个格子能对应多少个最后一行的格子。

然后再设置一个vis数组表示最后一行是否已经被到达过，如果最后一行有点还没有被到达过，就输出0和vis=0的格子数量

但是当我们想要实现的时候，发现如果第一行的某个点对应的最后一行的点是断断续续的，那就很舒（e）服（xin）了

buuuut~

似乎可以证明，对于每一个第一行的点，他所对应的最后一行的点总是连续的

反证法：假设可以不连续

我们来看图

如图，这是一条从上到下的连续的路径，用红色标记

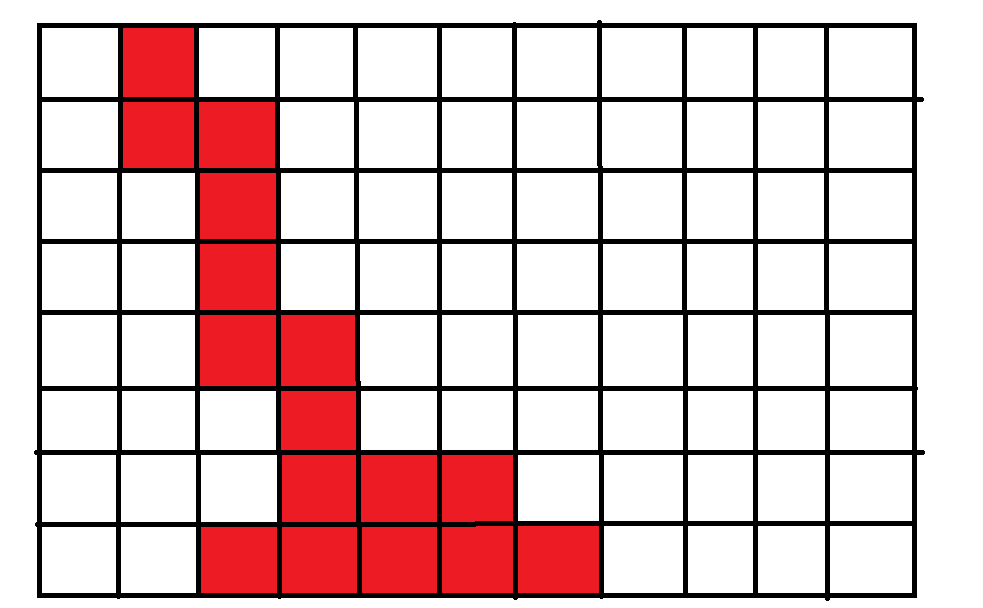
现在我们假设从第一行开始有这么一条路径不连续，如图，用蓝色表示

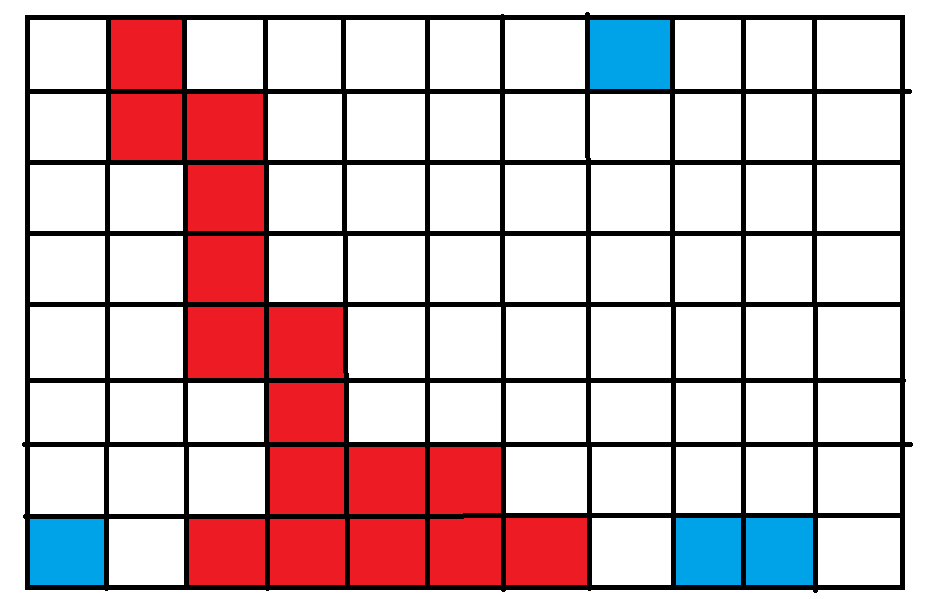
我们会发现，这样的话一定会有重合的路径，用紫色表示

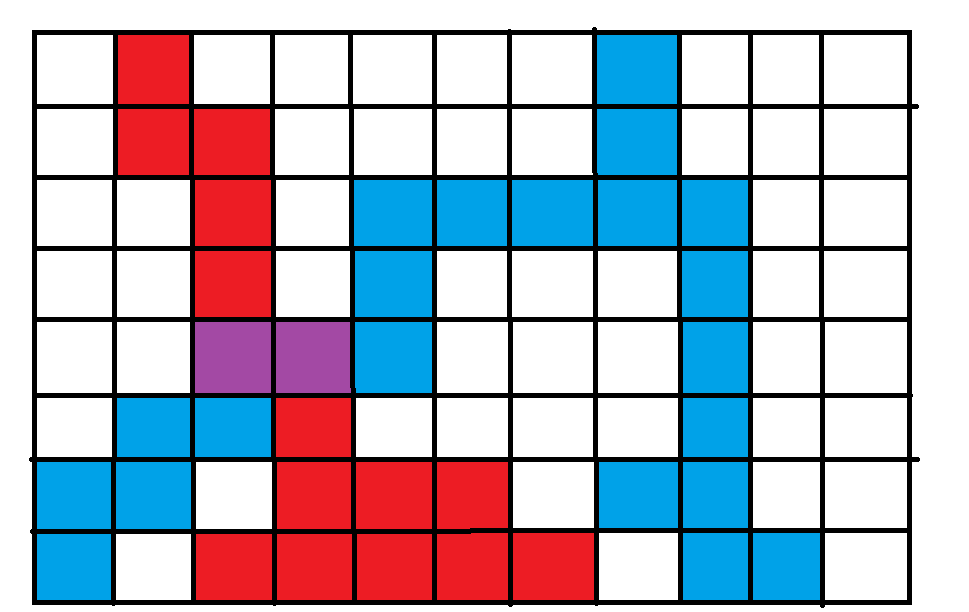
既然这样，从第一行蓝色点出发也一定能够到达最下层的红色点

那么最下面一行的区间一定是连续的，证毕（这里不连续是因为有无解的情况）

有了这个结论，只要不是无解的情况，把最后一行的连续区间拿出来，就变成了一个线段覆盖问题

代码：

 #include<iostream>
 #include<cstdio>
 #include<cstdlib>
 #include<algorithm>
 #include<cstring>
 #include<string>
 #include<queue>
 #include<stack>
 #include<time.h>
 using namespace std;
 typedef long long ll;
 ll read(){
     ll ans=;
     char last=' ',ch=getchar();
     while(ch<'' || ch>'')last=ch,ch=getchar();
     while(ch>='' && ch<='')ans=ans*+ch-'',ch=getchar();
     if(last=='-')ans=-ans;
     return ans;
 }

 const int maxn=;

 int n,m,atlas[maxn][maxn];
 int num[maxn][maxn];
 bool vis[maxn][maxn];
 int dx[]={,-,,},dy[]={,,,-};
 int l[maxn][maxn],r[maxn][maxn];

 //记忆化搜索
 void dfs(int x,int y)
 {
     vis[x][y]=true;//先标记这个点到达过
     for(int i=;i<;i++)//上下左右搜索
     {
         int nx=x+dx[i],ny=y+dy[i];
         if(nx<||nx>n||ny<||ny>m) continue;//判断边界
         if(atlas[nx][ny]>=atlas[x][y]) continue;//判断高度
         if(!vis[nx][ny])dfs(nx,ny);
         l[x][y]=min(l[x][y],l[nx][ny]);
         r[x][y]=max(r[x][y],r[nx][ny]);//更新区间左右端点
     }
 }

 int main()
 {
     n=read(),m=read();
     memset(vis,false,sizeof(vis));
     memset(l,0x3f,sizeof(l));//初始化
     for(int i=;i<=m;i++)
     {
         l[n][i]=r[n][i]=i;//区间初始化
     }
     for(int i=;i<=n;i++)
     {
         for(int j=;j<=m;j++)
         {
             atlas[i][j]=read();
         }
     }

     for(int i=;i<=m;i++)
     {
         if(!vis[][i]) dfs(,i);//如果还没有被到达过，就搜索
     }

     int counti=;
     for(int i=;i<=m;i++)
     {
         if(!vis[n][i]) counti++;
     }//看最后一行有没有不能到达的
     if(counti!=)
     {
        cout<<<<endl<<counti;
        return ;
     }

     int left=;//记录当前最左边的点
     while (left<=m)//跑一遍区间覆盖
     {
         int maxr=;
         for (int i=;i<=m;i++)
             if (l[][i]<=left)//如果这个点在区间左端点的右边
                 maxr=max(maxr,r[][i]);//寻找右端点最大的
         counti++;
         left=maxr+;//继续更新
     }
     cout<<<<endl<<counti;
     return ;
 }