AtCoder Regular Contest 071 D - 井井井 / ###

题目：http://arc071.contest.atcoder.jp/tasks/arc071_b

题意：

　　　　有一个二维的平面，给你x_n根竖线和y_m根横线，问这些线围成的长方形（正方形）的面积和（要求mod）。

　　　　例子：

　　　　　　3 3
　　　　　　1 3 4
　　　　　　1 3 6

　　　　

　　　　构成了9个长方体。

　　　　

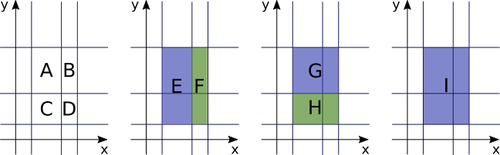
　　　　可以算出ans = 60；

题解：

　　　　　　　　很容易就可以想到暴击枚举 i,j,k,l，对应的每个值然后求面积。

　　　　　

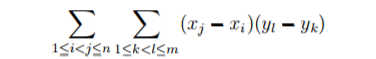
　　　　　　　　但是毫无疑问n⁴是会TLE的。

　　　　　　　　同样的答案等价于

　　　　

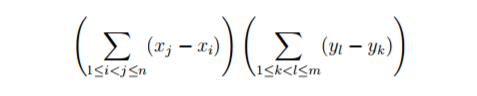
　　　　　　　　但是很不好意思，这样还是会TLE。

　　　　　　　　所以我们就可以把它化简为

　　　　　　　　

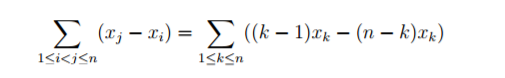
　　　　　　　————————————证明————————————

　　　　　　　　展开 ∑(x_j-x_i)为

　　　　　　　　(x₂-x₁)+(x₃-x₁)+····+(x_n-x₁)

　　　　　　　　(x₃-x₂)+(x₄-x₂)+···+（x_n-x₁）

　　　　　　　　···

　　　　　　　　不难发现当为第k个x的时候，在它前面有(k-1)个x要选择它，所以是 +（k-1）*x_k 。而在k的后面有（n-k）个x。x_k 要选它们，所以是 -（n-k）*x_k 。

　　　　　　　　就可以化简成∑((k-1)x_k-(n-k)x_k)。把复杂度从n²降到n。

　　　　　　　　同理y也是这样。

　　　　　　　　总的复杂度为O(_n+_m)。

　　　　　　　——————————————————————————

 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <cstdlib>
 #include <string>
 #include <vector>
 #include <map>
 #include <set>
 #include <queue>
 #include <sstream>
 #include <algorithm>
 using namespace std;
 #define pb push_back
 #define mp make_pair
 #define ms(a, b)  memset((a), (b), sizeof(a))
 //#define LOCAL
 typedef long long LL;
 const int inf = 0x3f3f3f3f;
 const int maxn = +;
 const int mod = 1e9+;
 LL x[maxn];
 LL y[maxn];
 int main()
 {
     #ifdef LOCAL
         freopen("input.txt" , "r", stdin);
     #endif // LOCAL
     int n, m;
     scanf("%d%d", &n, &m);
     for(int i=;i<=n;i++)   scanf("%lld", &x[i]);
     for(int i=;i<=m;i++)   scanf("%lld", &y[i]);
     LL ans =;
     LL sumx = , sumy=;
     for(int i=;i<=n;i++)
         sumx =(sumx+ ( (i-)*x[i] - (n-i)*x[i] )%mod)%mod;
     for(int i=;i<=m;i++)
         sumy =(sumy+ ( (i-)*y[i] - (m-i)*y[i] )%mod)%mod;
 //    printf("%lld %lld\n", sumx, sumy);
     printf("%lld\n", (sumx * sumy) %mod);
     return ;
 }