The Preliminary Contest for ICPC Asia Nanjing 2019（ B H F）

B. super_log

题意：研究一下就是求幂塔函数 %m的值。

思路：扩展欧拉降幂。

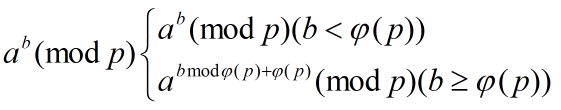
AC代码：

 #include<bits/stdc++.h>
 using namespace std;
 typedef long long ll;
 const long long mod = 1e9 + ;
 int a, b, m;
 ll eular(ll n)
 {
     ll ans = n;
     for(int i = ;i * i <= n;i++)
     {
         if(n % i == )
         {
             ans -= ans / i;
             while(n % i == ) n /= i;
         }
     }
     if(n != ) ans -= ans / n;
     return ans;
 }
 int ksm(ll a, ll n, ll mod)
 {
     if(n == ) return ;
     if(a <= ) return a;
     if (n == )
         return ;
     if (a<=)
         return a;
     bool flag = false;
     ll t = ;
     for (int i = ; i < n; i++)
     {
         t = t*a;
         if (t >= mod)
         {
             flag = true;
             break;
         }
     }
     ll ans = ;
     while (n)
     {
         if (n & )
         {
             ans *= a;
             ans %= mod;
         }
         a = a * a % mod;
         n >>= ;
     }
     if (flag)
     {
         ans += mod;
     }
     return ans;
 }
 ll dfs(int a,int b,ll mod)
 {
     if (b == )
         return ;
     if (b == )
         return a;
     if (mod == )
         return ;
     ll h1 = ksm(a, dfs(a, b-, eular(mod)),mod);
     return h1;
 }
 int main()
 {
     int t;
     cin >>t;
     while(t--)
     {
         cin >> a >> b >> m;
         cout << dfs(a, b, m) % m << endl;
     }
     return ;
 }

F. Greedy Sequence

题意：题意好绕的啊，自己看吧。

思路：用线段树查询区间最大值，因为对于每个数 i，只有比他小的数才有用，所以从小到大枚举，在线段树中（此时所有值都小于 i ）。

AC代码：

 #include<bits/stdc++.h>
 using namespace std;
 #define lson l , m , rt << 1
 #define rson m + 1, r, rt << 1 | 1
 #define ls rt << 1
 #define rs rt << 1 | 1
 #define lr2 (l + r) / 2
 const int maxn = 1e5+ ;
 int n, k, a[maxn], pos[maxn];
 int ans[maxn];
 int sum[maxn* ] ;
 void up(int rt){
     sum[rt] = max(sum[ls], sum[rs]);
 }
 void build(int l ,int r, int rt)
 {
     sum[rt] = ;
     if(l == r) return ;
     int m = lr2;
     build(lson);
     build(rson);
     up(rt);
 }
 int query(int a, int b, int l, int r, int rt)
 {
     if(a <= l && b >= r) return sum[rt];
     int ans = ;
     int m = lr2;
     if(a <= m) ans = max(ans,query(a, b, lson));
     if(b > m) ans = max(ans, query(a, b, rson));
     return ans;
 }
 void update(int k, int v, int l, int r, int rt)
 {
     if(l == r){
         sum[rt] = v;
         return;
     }
     int m = lr2;
     if(k <= m) update(k, v, lson);
     else update(k, v, rson);
     up(rt);
 }
 int main()
 {
     std::ios::sync_with_stdio(false);
     int t;
     cin >> t;
     while(t--)
     {
         cin >> n >> k;
         for(int i = ;i <= n;i++){
             cin >> a[i];
             pos[a[i]] = i;
         }
         build(, n, );
         for(int i = ;i <= n;i++)
         {
             int l = max(, pos[i] - k);
             int r = min(n, pos[i] + k);
             int x = query(l, r , , n, );
             update(pos[i], i, , n, );
             ans[i] = ans[x] + ;
         }
         for(int i = ;i <= n;i++){
             cout << ans[i];
             if(i == n)cout << endl;
             else cout << " ";
         }
     }
     return ;
 }

---

H. Holy Grail

题意：给你一张n点m边的有向图，无重边，无负加权循环。请你加6对顶点，请你加6条权值最小的边使之没有负圈。

思路：每给一对顶点，跑一遍最短路，没有负环的条件是没有一条来的路和加的边加起来为负，所以每次加的边和答案为反向最短路。

AC代码：

 #include<iostream>
 #include<cstdio>
 #include<vector>
 #include<queue>
 #include<cstring>
 #include<algorithm>
 using namespace std;
 const int maxn = 1e5+;
 const int INF = 0x3f3f3f3f;
 typedef long long ll;
 typedef pair<ll,int> P;
 int n,m;
 struct edge{
     int to;
     ll cost;
 }es[maxn];
 vector <edge> G[maxn];
 ll d[maxn];
 void dijkstra(int s)
 {
     priority_queue<P,vector<P>,greater<P> > que;
     fill(d,d+m+,INF);
     d[s] = ;
     que.push(P(,s));
     while(!que.empty())
     {
         P p= que.top();que.pop();
         int v = p.second;
         if(d[v] < p.first) continue;
         for(int i = ;i < G[v].size();i++)
         {
             edge e = G[v][i];;
             if(d[e.to] > d[v] + e.cost)
             {

                 d[e.to]= d[v] + e.cost;
                 que.push(P(d[e.to],e.to));
             }
         }
     }
 }
 int main()
 {
     std::ios::sync_with_stdio(false);
     std::cin.tie();std::cout.tie();
     int t;
     cin >> t;
     while(t--)
     {
         cin >> n >> m;
         for(int i = ;i <= n;i++)G[i].clear();
         int count = ;
         int a,b,c;
         for(int i = ;i < m;i++)
         {
            cin >> a >> b >> c;
             es[count].to = b;
             es[count].cost = c;
             G[a].push_back(es[count++]);
         }
         for(int i = ;i < ;i++){
             cin >> a >> b;
             dijkstra(b);
             cout << -d[a] << endl;
             es[count].to = b;
             es[count].cost = -d[a];
             G[a].push_back(es[count++]);
         }

     }

     return ;
 }