Java数据结构与算法(1):线性表

线性表是一种简单的数据类型，它是具有相同类型的n个数据元素组成的有限序列。形如如A₀，A₁，...，A_n-1。大小为0的表为空表，称A_i后继A_i-1，并称A_i-1前驱A_i。

printList打印出表元素，makeEmpty置空表，find返回某一项首次出现的位置，insert和remove一般是从表的某个位置插入和删除某个元素；而findKth则返回某个位置上的元素，next和previous会取一个位置作为参数返回前驱元和后继元的值。

表的数组实现

对表的所有操作都可以通过数组实现。数组的存储示意图如下：

这种存储结构的特点是：数据是连续的，随机访问速度快。printList以线性时间执行，findKth操作则话费常数时间。对于插入和删除来说效率是比较低下的，最坏情况下，在位置0的插入需要将所有元素向后移动一个位置。

基于数组的链表实现：

public class MyArrayList<T> implements Iterable<T>{

    private static final int DEFAULT_CAPACITY=10;
    private int size;
    private T[] items;

    public MyArrayList() {
        doClear();
    }

    public void clear() {
        doClear();
    }

    public int size() {
        return size;
    }

    public boolean isEmpty() {
        return size == 0;
    }

    public void trimToSize() {
        ensureCapacity(size);
    }

    public boolean add(T x) {
        add(size, x);
        return true;
    }

    public void add(int idx, T x) {
        if (items.length == size) {
            ensureCapacity(size * 2 + 1);
        }
        for (int i = size; i > idx; i--) {
            items[i] = items[i - 1];
        }
        items[idx] = x;
        size++;
    }

    public T remove(int idx) {
        T removedItem = items[idx];
        for (int i = idx; i < size - 1; i++) {
            items[i] = items[i + 1];
        }
        size--;
        return removedItem;
    }

    private void doClear() {
        size = 10;
        ensureCapacity(DEFAULT_CAPACITY);
    }

    private void ensureCapacity(int newCapacity) {
        if (newCapacity < size) {
            return;
        }
        T[] old = items;
        items = (T[]) new Object[newCapacity];
        for (int i = 0; i < size; i++) {
            items[i] = old[i];
        }
    }

    public Iterator<T> iterator() {
        return new ArrayListIterator();
    }

    private class ArrayListIterator implements Iterator<T> {
        private int current = 0;

        @Override
        public boolean hasNext() {
            return current < size;
        }

        @Override
        public T next() {
            if (!hasNext())
                throw new NoSuchElementException();
            return items[current++];
        }

        public void remove() {
            MyArrayList.this.remove(--current);
        }
    }
}

单链表

当需要对表进行频繁的插入删除操作时，数组的实现方式就显得效率过低了。链表由一些列节点组成，这些节点不必在内存中相连。每一个节点均含有表元素和到包含该元素后继元的节点的链。单链表的存储示意图如下：

remove操作只需要移动next引用即可实现：

insert方法需要先添加一个节点，然后执行两次引用的调整：

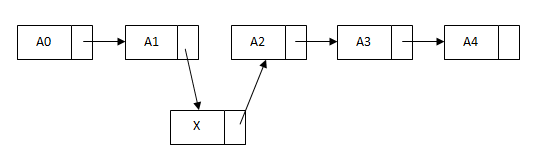
单链表的特点：节点的链接方向是单向的；相对于数组，单链表的随机访问速度较慢，添加、删除效率较高。

双向链表

双向链表与单向链表结构相似，由数据元素和两个链组成，这两个链分别指向该节点的前驱和后继。一般构建为双向循环链表，即最后一个节点的next链指向链表的第一个元素，第一个节点的previous链指向链表的最后一个元素。存储结构如下：

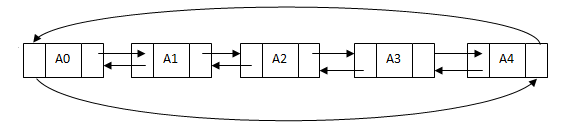
双向链表删除：

双向链表的添加就是删除的一个逆过程，不再画图了。

双向链表实现：

public class DoubleLink<T> {
    // 表头
    private Node<T> head;
    // 节点数
    private int count;

    private class Node<T> {
        public Node prev; // 前节点
        public Node next; // 后节点
        public T value;

        public Node(T value, Node prev, Node next) {
            this.prev = prev;
            this.next = next;
            this.value = value;
        }
    }

    public DoubleLink() {
        // 创建表头
        head = new Node<>(null, null, null);
        head.prev = head.next = head;
        count = 0;
    }

    // 节点数
    public int size() {
        return count;
    }

    // 判断表是否为空
    public boolean isEmpty() {
        return count == 0;
    }

    // 获取第index位置的节点
    private Node<T> getNode(int index) {
        if (index < 0 || index >= count) {
            throw new IndexOutOfBoundsException();
        }
        // 正向查找
        if (index <= count / 2) {
            Node<T> node = head.next;
            for (int i = 0; i < index; i++) {
                node = node.next;
            }
            return node;
        }
        // 反向查找
        Node<T> rnode = head.prev;
        int rindex = count - index - 1;
        for (int j = 0; j < rindex; j++) {
            rnode = rnode.prev;
        }
        return rnode;
    }

    // 获取第index位置节点的值
    public T get(int index) {
        return getNode(index).value;
    }

    // 将节点插入到index位置
    public void insert(int index, T t) {
        if (index == 0) {
            Node node = new Node(t, head, head.next);
            head.next.prev = node;
            head.next = node;
            count++;
            return;
        }
        Node<T> inode = getNode(index);
        // 创建新节点
        Node<T> newNode = new Node<>(t, inode.prev, inode);
        inode.prev.next = newNode;
        inode.next = newNode;
        return;
    }

    // 删除节点
    public Node<T> delete(int index) {
        Node<T> delNode = getNode(index);
        delNode.prev.next = delNode.next;
        delNode.next.prev = delNode.prev;
        count--;
        return delNode;
    }
}