Codeforces 916E(思维+dfs序+线段树+LCA)

题面

传送门

题目大意:给定初始根节点为1的树,有3种操作

1.把根节点更换为r

2.将包含u,v的节点的最小子树(即lca(u,v)的子树)所有节点的值+x

3.查询v及其子树的值之和

分析

看到批量修改子树,我们想到将树上操作转化为区间操作

通过DFS序我们可以实现这一点.

对于每个节点x,我们记录它在前序遍历中的位置l[x],再一次回到x时的序号r[x],则x及其子树的区间为前序遍历中的[l[x],r[x]]

具体可点击这篇博客

那么,3种操作如何进行:

操作1.用一个变量root记录当前根即可,时间复杂度O(1)" role="presentation" style="position: relative;">O(1)O(1)

以下求LCA,DFS序,子树,以及修改等操作都在初始的树上进行,再想办法将它转换为根不是1的情况

操作2.由于根节点变化,需要分类讨论

首先,定义三个点的LCA值lca(u,v,w)为lca(u,v),lca(u,w),lca(v,w)中深度最深的那一个

设修改的点为u,v,根节点为root

(1) 若lca(u,v)在root的子树中



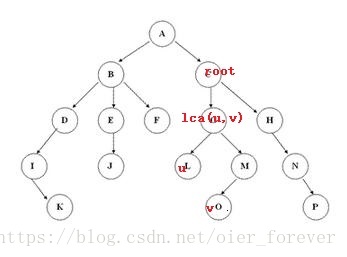
显然结果和根为1的情况一样,直接修改即可,时间复杂度O(log2n)" role="presentation" style="position: relative;">O(log2n)O(log2n)

(2)若lca(u,v,root)=root



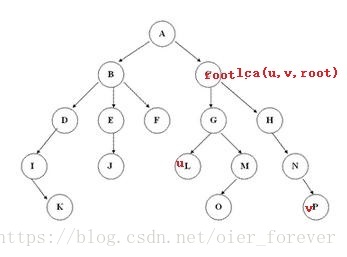
很明显包含u,v的最小子树就是整棵树,所以修改整棵树,时间复杂度O(log2n)" role="presentation" style="position: relative;">O(log2n)O(log2n)

(3)若root在lca(u,v,root)的子树中



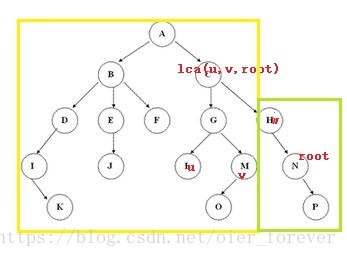
此时可采用类似容斥原理的方法

先将整棵树的值+x

再找到root的祖先中离lca(u,v,root)最近的整数w,将w及其子树(绿色部分)的值-x,剩下的就是包含u,v的最小子树了(黄色部分)

求w可用树上倍增,时间复杂度O(log2n)" role="presentation" style="position: relative;">O(log2n)O(log2n)

操作3.

类似操作2的分类讨论

设查询的点为u,根节点为root

(1)若u在root的子树中,则直接查询u的子树

(2)若u=root,查询整棵树

(3)若root在u的子树中



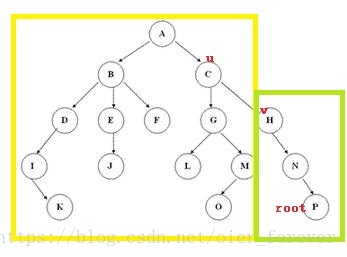
先查询整棵树的值之和,再找root的祖先中距离u最近的一个v

用整棵树的值之和-v及子树的值之和(绿色部分)=所求(黄色部分)

代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#define maxn 100005
#define maxlog 32
using namespace std;
inline int qread(){
    int x=0,sign=1;
    char c=getchar();
    while(c<'0'||c>'9'){
        if(c=='-') sign=-1;
        c=getchar();
    }
    while(c>='0'&&c<='9'){
        x=x*10+c-'0';
        c=getchar();
    }
    return x*sign;
}

int n,q;
int a[maxn];
int root=1;

struct edge{
    int from;
    int to;
    int next;
}E[maxn<<1];
int head[maxn];
int size=0;
void add_edge(int u,int v){
    size++;
    E[size].from=u;
    E[size].to=v;
    E[size].next=head[u];
    head[u]=size;
}

int cnt;
int log2n;
int l[maxn],r[maxn];
int deep[maxn],anc[maxn][maxlog];
void dfs(int x,int fa){
    l[x]=++cnt;
    anc[x][0]=fa;
    for(int i=1;i<=log2n;i++){
        anc[x][i]=anc[anc[x][i-1]][i-1];
    }
    for(int i=head[x];i;i=E[i].next){
        int y=E[i].to;
        if(y!=fa){
            deep[y]=deep[x]+1;
            dfs(y,x);
        }
    }
    r[x]=cnt;
}

int lca(int x,int y){
    if(deep[x]<deep[y]) swap(x,y);
    for(int i=log2n;i>=0;i--){
        if(deep[anc[x][i]]>=deep[y]){
            x=anc[x][i];
        }
    }
    if(x==y) return x;
    for(int i=log2n;i>=0;i--){
        if(anc[x][i]!=anc[y][i]){
            x=anc[x][i];
            y=anc[y][i];
        }
    }
    return anc[x][0];
}

int tri_lca(int u,int v,int r){
    int l1=lca(u,v);
    int l2=lca(u,r);
    int l3=lca(v,r);
    int max_deep=max(deep[l1],max(deep[l2],deep[l3]));
    if(deep[l1]==max_deep) return l1;
    else if(deep[l2]==max_deep) return l2;
    else return l3;
}

int get_close(int w,int r){
    int x=r;
    for(int i=log2n;i>=0;i--){
        if(deep[anc[x][i]]>deep[w]){
            x=anc[x][i];
        }
    }
    return x;
}
struct node{
    int l;
    int r;
    long long v;
    long long mark;
    int len(){
        return r-l+1;
    }
}tree[maxn<<2];
void push_up(int pos){
    tree[pos].v=tree[pos<<1].v+tree[pos<<1|1].v;
}
void build(int l,int r,int pos){
    tree[pos].l=l;
    tree[pos].r=r;
    tree[pos].v=0;
    tree[pos].mark=0;
    if(l==r) return;
    int mid=(l+r)>>1;
    build(l,mid,pos<<1);
    build(mid+1,r,pos<<1|1);
}
void push_down(int pos){
    if(tree[pos].mark){
        tree[pos<<1].mark+=tree[pos].mark;
        tree[pos<<1|1].mark+=tree[pos].mark;
        tree[pos<<1].v+=tree[pos].mark*tree[pos<<1].len();
        tree[pos<<1|1].v+=tree[pos].mark*tree[pos<<1|1].len();
        tree[pos].mark=0;
    }
}
void update(int L,int R,long long v,int pos){
    if(L<=tree[pos].l&&R>=tree[pos].r){
        tree[pos].mark+=v;
        tree[pos].v+=(v*tree[pos].len());
        return;
    }
    push_down(pos);
    int mid=(tree[pos].l+tree[pos].r)>>1;
    if(L<=mid) update(L,R,v,pos<<1);
    if(R>mid) update(L,R,v,pos<<1|1);
    push_up(pos);
}
long long query(int L,int R,int pos){
    if(L<=tree[pos].l&&R>=tree[pos].r){
        return tree[pos].v;
    }
    push_down(pos);
    int mid=(tree[pos].l+tree[pos].r)>>1;
    long long ans=0;
    if(L<=mid) ans+=query(L,R,pos<<1);
    if(R>mid) ans+=query(L,R,pos<<1|1);
    return ans;
}

void change(int u,int v,int x){
    int xx=lca(u,v);
    int lca_num=tri_lca(u,v,root);
    if(l[root]<l[xx]||r[root]>r[xx]){
        update(l[xx],r[xx],x,1);
        return;
    }else if(lca_num==root){
        update(1,n,x,1);
        return;
    }else{
        int w2=get_close(lca_num,root);
        update(1,n,x,1);
        update(l[w2],r[w2],-x,1);
        return;
    }
}

long long sum(int w){
    if(l[root]<l[w]||r[root]>r[w]){
        return query(l[w],r[w],1);
    }else{
        if(w==root){
            return query(1,n,1);
        }
        int sonw=get_close(w,root);
//      printf("%d\n",query(1,n,1));
//      printf("%d\n",query(l[sonw],r[sonw],1));
        return query(1,n,1)-query(l[sonw],r[sonw],1);
    }
}

int main(){
    int u,v,cmd,x;
    n=qread();
    q=qread();
    for(int i=1;i<=n;i++) a[i]=qread();
    for(int i=1;i<n;i++){
        u=qread();
        v=qread();
        add_edge(u,v);
        add_edge(v,u);
    }
    deep[1]=1;
    log2n=log2(n)+1;
    dfs(1,0);
    build(1,n,1);
    for(int i=1;i<=n;i++){
        update(l[i],l[i],a[i],1);
    }
    for(int i=1;i<=q;i++){
        cmd=qread();
        if(cmd==1){
            v=qread();
            root=v;
        }else if(cmd==2){
            u=qread();
            v=qread();
            x=qread();
            change(u,v,x);
        }else{
            v=qread();
            printf("%I64d\n",sum(v));
        }
//      printf("debug: sum=%d\n",query(1,n,1));
    }
    return 0;
}