2023-03-11：给定一个N*M的二维矩阵，只由字符‘O‘、‘X‘、‘S‘、‘E‘组成， ‘O‘表示这个地方是可通行的平地， ‘X‘表示这个地方是不可通行的障碍， ‘S‘表示这个地方有一个士兵，全

2023-03-11：给定一个N*M的二维矩阵，只由字符’O’、‘X’、‘S’、'E’组成，
'O’表示这个地方是可通行的平地，
'X’表示这个地方是不可通行的障碍，
'S’表示这个地方有一个士兵，全图保证只有一个士兵，
'E’表示这个地方有一个敌人，全图保证只有一个敌人，
士兵可以在上、下、左、右四个方向上移动，
走到相邻的可通行的平地上，走一步耗费a个时间单位，
士兵从初始地点行动时，不管去哪个方向，都不用耗费转向的代价，
但是士兵在行动途中，如果需要转向，需要额外再付出b个时间单位。
返回士兵找到敌人的最少时间。
如果因为障碍怎么都找不到敌人，返回-1，
1 <= N,M <= 1000，
1 <= a,b <= 100000，
只会有一个士兵、一个敌人。
来自华为。

答案2023-03-11：

Dijkstra算法+优先级队列。

代码根据山寨版chatgpt稍做修改写的。这不得不承认chatgpt很强大，这还是山寨版的，感觉比我自己写得还要好。

以下代码是生成的rust代码，稍微做了修改。如下：

use rand::Rng;
use std::cmp::Reverse;
use std::collections::BinaryHeap;
fn random_map(n: usize, m: usize) -> Vec<Vec<char>> {
    let mut map = vec![vec!['O'; m]; n];
    for i in 0..n {
        for j in 0..m {
            if rand::thread_rng().gen_range(0, 2) == 0 {
                map[i][j] = 'X';
            }
        }
    }
    let si = rand::thread_rng().gen_range(0, n);
    let sj = rand::thread_rng().gen_range(0, m);
    map[si][sj] = 'S';
    let (mut ei, mut ej) = (si, sj);
    while ei == si && ej == sj {
        ei = rand::thread_rng().gen_range(0, n);
        ej = rand::thread_rng().gen_range(0, m);
    }
    map[ei][ej] = 'E';
    map
}

fn main() {
    let n = 3;
    let m = 4;
    let v = 10;
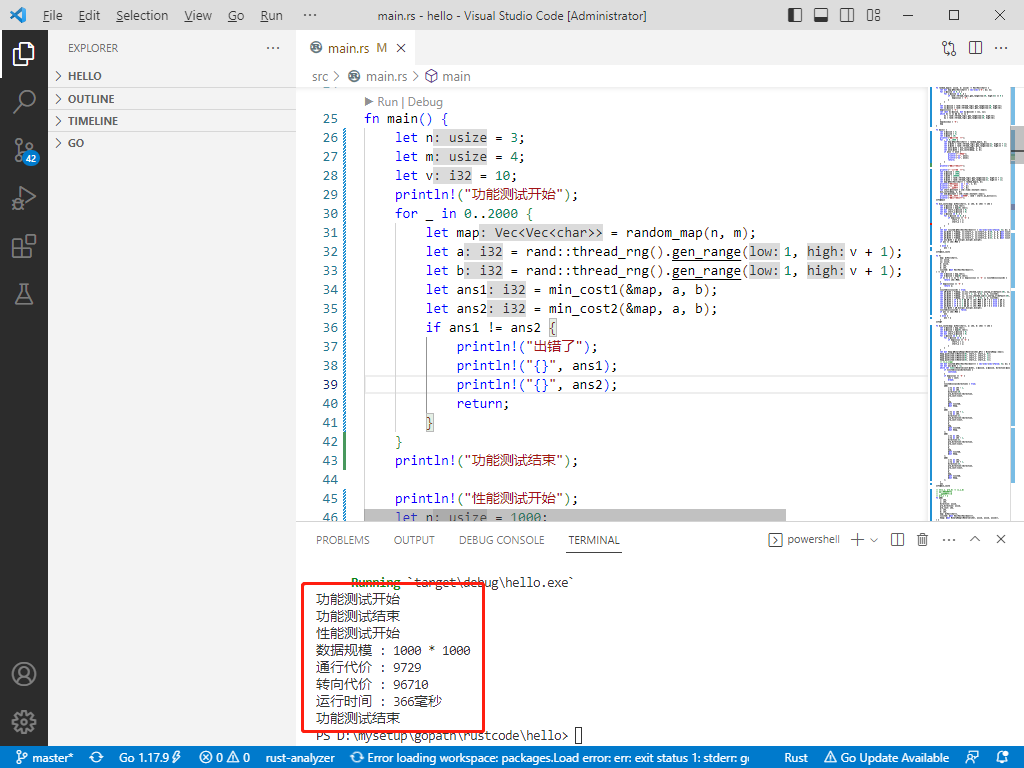
    println!("功能测试开始");
    for _ in 0..2000 {
        let map = random_map(n, m);
        let a = rand::thread_rng().gen_range(1, v + 1);
        let b = rand::thread_rng().gen_range(1, v + 1);
        let ans1 = min_cost1(&map, a, b);
        let ans2 = min_cost2(&map, a, b);
        if ans1 != ans2 {
            println!("出错了");
            println!("{}", ans1);
            println!("{}", ans2);
            return;
        }
    }
    println!("功能测试结束");

    println!("性能测试开始");
    let n = 1000;
    let m = 1000;
    let v = 100000;
    let a = rand::thread_rng().gen_range(1, v + 1);
    let b = rand::thread_rng().gen_range(1, v + 1);
    let map = random_map(n, m);
    println!("数据规模 : {} * {}", n, m);
    println!("通行代价 : {}", a);
    println!("转向代价 : {}", b);
    let start = std::time::Instant::now();
    min_cost2(&map, a, b);
    let end = std::time::Instant::now();
    println!("运行时间 : {}毫秒", (end - start).as_millis());
    println!("功能测试结束");
}

fn min_cost1(map: &[Vec<char>], a: i32, b: i32) -> i32 {
    let n = map.len();
    let m = map[0].len();
    let mut start_x = 0;
    let mut start_y = 0;
    for i in 0..n {
        for j in 0..m {
            if map[i][j] == 'S' {
                start_x = i;
                start_y = j;
            }
        }
    }
    let mut visited = vec![vec![vec![false; 4]; m]; n];
    let p1 = f(&map, start_x, start_y, 0, a, b, &mut visited);
    let p2 = f(&map, start_x, start_y, 1, a, b, &mut visited);
    let p3 = f(&map, start_x, start_y, 2, a, b, &mut visited);
    let p4 = f(&map, start_x, start_y, 3, a, b, &mut visited);
    let ans = p1.min(p2).min(p3).min(p4);
    if ans == i32::MAX {
        -1
    } else {
        ans - a
    }
}

fn f(
    map: &[Vec<char>],
    si: usize,
    sj: usize,
    d: usize,
    a: i32,
    b: i32,
    visited: &mut Vec<Vec<Vec<bool>>>,
) -> i32 {
    let n = map.len();
    let m = map[0].len();
    if si >= n || sj >= m || map[si][sj] == 'X' || visited[si][sj][d] {
        return i32::MAX;
    }
    if map[si][sj] == 'E' {
        return a;
    }
    visited[si][sj][d] = true;
    let p0 = f(&map, si.checked_sub(1).unwrap_or(0), sj, 0, a, b, visited);
    let p1 = f(&map, si + 1, sj, 1, a, b, visited);
    let p2 = f(&map, si, sj.checked_sub(1).unwrap_or(0), 2, a, b, visited);
    let p3 = f(&map, si, sj + 1, 3, a, b, visited);
    let p0 = if d != 0 && p0 != i32::MAX { p0 + b } else { p0 };
    let p1 = if d != 1 && p1 != i32::MAX { p1 + b } else { p1 };
    let p2 = if d != 2 && p2 != i32::MAX { p2 + b } else { p2 };
    let p3 = if d != 3 && p3 != i32::MAX { p3 + b } else { p3 };
    let ans = p0.min(p1).min(p2).min(p3);
    visited[si][sj][d] = false;
    if ans == i32::MAX {
        ans
    } else {
        ans + a
    }
}

fn min_cost2(map: &[Vec<char>], a: i32, b: i32) -> i32 {
    let n = map.len();
    let m = map[0].len();
    let mut start_x = 0;
    let mut start_y = 0;
    for i in 0..n {
        for j in 0..m {
            if map[i][j] == 'S' {
                start_x = i;
                start_y = j;
            }
        }
    }
    let mut heap = BinaryHeap::new();
    heap.push((Reverse(0), start_x, start_y, 0));
    heap.push((Reverse(0), start_x, start_y, 1));
    heap.push((Reverse(0), start_x, start_y, 2));
    heap.push((Reverse(0), start_x, start_y, 3));
    // (i,j,朝向)
    let mut visited = vec![vec![vec![false; 4]; m]; n];
    let mut ans = -1;
    while let Some((Reverse(cost), x, y, direction)) = heap.pop() {
        if visited[x][y][direction] {
            continue;
        }
        if map[x][y] == 'E' {
            ans = cost;
            break;
        }
        visited[x][y][direction] = true;
        add(
            x as i32 - 1,
            y as i32,
            0,
            direction,
            cost,
            a,
            b,
            map,
            &mut visited,
            &mut heap,
        );
        add(
            x as i32 + 1,
            y as i32,
            1,
            direction,
            cost,
            a,
            b,
            map,
            &mut visited,
            &mut heap,
        );
        add(
            x as i32,
            y as i32 - 1,
            2,
            direction,
            cost,
            a,
            b,
            map,
            &mut visited,
            &mut heap,
        );
        add(
            x as i32,
            y as i32 + 1,
            3,
            direction,
            cost,
            a,
            b,
            map,
            &mut visited,
            &mut heap,
        );
    }
    ans
}

// 从(x,y, pre_d) -> (i,j,d)
// 走格子的代价a
// 转向的代价是b
// pre_c + a
fn add(
    i: i32,
    j: i32,
    direction: usize,
    pre_direction: usize,
    pre_cost: i32,
    a: i32,
    b: i32,
    map: &[Vec<char>],
    visited: &mut Vec<Vec<Vec<bool>>>,
    heap: &mut BinaryHeap<(Reverse<i32>, usize, usize, usize)>,
) {
    let n = map.len() as i32;
    let m = map[0].len() as i32;
    if i < 0
        || i >= n
        || j < 0
        || j >= m
        || map[i as usize][j as usize] == 'X'
        || visited[i as usize][j as usize][direction]
    {
        return;
    }
    let mut cost = pre_cost + a;
    if direction != pre_direction {
        cost += b;
    }
    heap.push((Reverse(cost), i as usize, j as usize, direction));
}

以下代码是生成的golang代码，稍微做了修改。如下：

package main

import (
	"container/heap"
	"fmt"
	"math/rand"
	"time"
)

func minCost1(mapData [][]byte, a int, b int) int {
	// 获取地图大小和起点位置
	n, m := len(mapData), len(mapData[0])
	startX, startY := 0, 0
	for i := 0; i < n; i++ {
		for j := 0; j < m; j++ {
			if mapData[i][j] == 'S' {
				startX, startY = i, j
				break
			}
		}
	}

	// 初始化 visited 数组
	visited := make([][][]bool, n)
	for i := range visited {
		visited[i] = make([][]bool, m)
		for j := range visited[i] {
			visited[i][j] = make([]bool, 4)
		}
	}

	// 计算从四个方向到达终点的最短距离
	p1 := f(mapData, startX, startY, 0, a, b, visited)
	p2 := f(mapData, startX, startY, 1, a, b, visited)
	p3 := f(mapData, startX, startY, 2, a, b, visited)
	p4 := f(mapData, startX, startY, 3, a, b, visited)

	// 返回四个方向中最小的距离
	ans := min(p1, min(p2, min(p3, p4)))
	if ans == 1<<31-1 {
		return -1
	} else {
		return ans - a
	}
}

func f(mapData [][]byte, si int, sj int, d int, a int, b int, visited [][][]bool) int {
	// 如果出现越界、墙壁或者已经访问过的情况，返回一个大整数表示无法到达该位置
	if si < 0 || si == len(mapData) || sj < 0 || sj == len(mapData[0]) || mapData[si][sj] == 'X' || visited[si][sj][d] {
		return 1<<31 - 1
	}

	// 如果到达终点，返回 a 表示到达终点所需的代价
	if mapData[si][sj] == 'E' {
		return a
	}

	// 标记该位置已经被访问过
	visited[si][sj][d] = true

	// 计算从四个方向到达下一个位置所需的代价（如果可以到达的话）
	var p [4]int
	p[0] = f(mapData, si-1, sj, 0, a, b, visited)
	p[1] = f(mapData, si+1, sj, 1, a, b, visited)
	p[2] = f(mapData, si, sj-1, 2, a, b, visited)
	p[3] = f(mapData, si, sj+1, 3, a, b, visited)
	if d != 0 && p[0] != 1<<31-1 {
		p[0] += b
	}
	if d != 1 && p[1] != 1<<31-1 {
		p[1] += b
	}
	if d != 2 && p[2] != 1<<31-1 {
		p[2] += b
	}
	if d != 3 && p[3] != 1<<31-1 {
		p[3] += b
	}

	// 返回四个方向中最小的代价，并且取消对该位置的访问标记
	ans := min(p[0], min(p[1], min(p[2], p[3])))
	visited[si][sj][d] = false
	if ans == 1<<31-1 {
		return ans
	} else {
		return ans + a
	}
}

func min(a int, b int) int {
	if a < b {
		return a
	} else {
		return b
	}
}

func minCost2(mapData [][]byte, a int, b int) int {
	// 获取地图大小和起点位置
	n, m := len(mapData), len(mapData[0])
	startX, startY := 0, 0
	for i := 0; i < n; i++ {
		for j := 0; j < m; j++ {
			if mapData[i][j] == 'S' {
				startX, startY = i, j
				break
			}
		}
	}

	// 初始化优先队列和 visited 数组
	h := &minHeap{}
	heap.Init(h)
	heap.Push(h, node{startX, startY, 0, 0})
	heap.Push(h, node{startX, startY, 1, 0})
	heap.Push(h, node{startX, startY, 2, 0})
	heap.Push(h, node{startX, startY, 3, 0})

	visited := make([][][]bool, n)
	for i := range visited {
		visited[i] = make([][]bool, m)
		for j := range visited[i] {
			visited[i][j] = make([]bool, 4)
		}
	}

	// 运行 Dijkstra 算法并返回答案
	ans := -1
	for h.Len() > 0 {
		cur := heap.Pop(h).(node)
		if visited[cur.x][cur.y][cur.dir] {
			continue
		}
		if mapData[cur.x][cur.y] == 'E' {
			ans = cur.cost
			break
		}
		visited[cur.x][cur.y][cur.dir] = true
		add(cur.x-1, cur.y, 0, cur.dir, cur.cost, a, b, mapData, visited, h)
		add(cur.x+1, cur.y, 1, cur.dir, cur.cost, a, b, mapData, visited, h)
		add(cur.x, cur.y-1, 2, cur.dir, cur.cost, a, b, mapData, visited, h)
		add(cur.x, cur.y+1, 3, cur.dir, cur.cost, a, b, mapData, visited, h)
	}

	return ans
}

type node struct {
	x, y, dir, cost int
}

type minHeap []node

func (h minHeap) Len() int { return len(h) }

func (h minHeap) Less(i, j int) bool { return h[i].cost < h[j].cost }

func (h minHeap) Swap(i, j int) { h[i], h[j] = h[j], h[i] }

func (h *minHeap) Push(x interface{}) { *h = append(*h, x.(node)) }

func (h *minHeap) Pop() interface{} {
	old := *h
	n := len(old)
	x := old[n-1]
	*h = old[:n-1]
	return x
}

func add(i, j, d, preD, preC, a, b int, mapData [][]byte, visited [][][]bool, h *minHeap) {
	if i < 0 || i == len(mapData) || j < 0 || j == len(mapData[0]) || mapData[i][j] == 'X' || visited[i][j][d] {
		return
	}
	cost := preC + a
	if d != preD {
		cost += b
	}
	heap.Push(h, node{i, j, d, cost})
}

func randomMap(n, m int) [][]byte {
	mapData := make([][]byte, n)
	for i := range mapData {
		mapData[i] = make([]byte, m)
		for j := range mapData[i] {
			if rand.Float32() < 0.5 {
				mapData[i][j] = 'O'
			} else {
				mapData[i][j] = 'X'
			}
		}
	}
	si := rand.Intn(n)
	sj := rand.Intn(m)
	mapData[si][sj] = 'S'
	var ei, ej int
	for {
		ei = rand.Intn(n)
		ej = rand.Intn(m)
		if ei != si || ej != sj {
			break
		}
	}
	mapData[ei][ej] = 'E'
	return mapData
}

func main() {
	n, m := 3, 4
	v := 10
	fmt.Println("功能测试开始")
	for i := 0; i < 2000; i++ {
		mapData := randomMap(n, m)
		a := rand.Intn(v) + 1
		b := rand.Intn(v) + 1
		ans1 := minCost1(mapData, a, b)
		ans2 := minCost2(mapData, a, b)
		if ans1 != ans2 {
			fmt.Println("出错了")
			fmt.Println(ans1)
			fmt.Println(ans2)
		}
	}
	fmt.Println("功能测试结束")

	fmt.Println("性能测试开始")
	n = 1000
	m = 1000
	v = 100000
	a := rand.Intn(v) + 1
	b := rand.Intn(v) + 1
	mapData := randomMap(n, m)
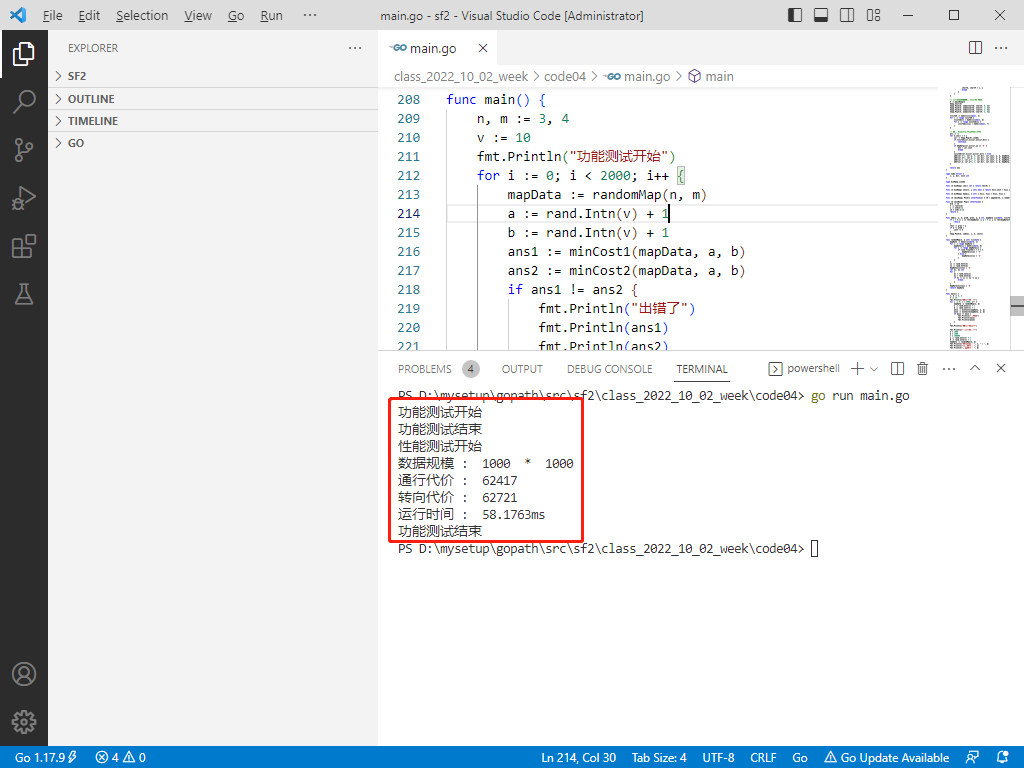
	fmt.Println("数据规模 : ", n, " * ", m)
	fmt.Println("通行代价 : ", a)
	fmt.Println("转向代价 : ", b)
	start := time.Now()
	minCost2(mapData, a, b)
	end := time.Now()
	fmt.Println("运行时间 : ", end.Sub(start))
	fmt.Println("功能测试结束")
}