西湖论剑2023-mp3[wp]

一 题目描述

二 解题步骤

1.分析文件

（1）放入Audacity中查看频谱信息无果

（2）010editor中查看文件结构

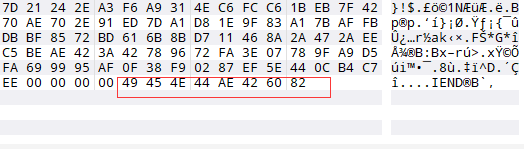
文件尾部存在PNG文件尾，搜索png文件头

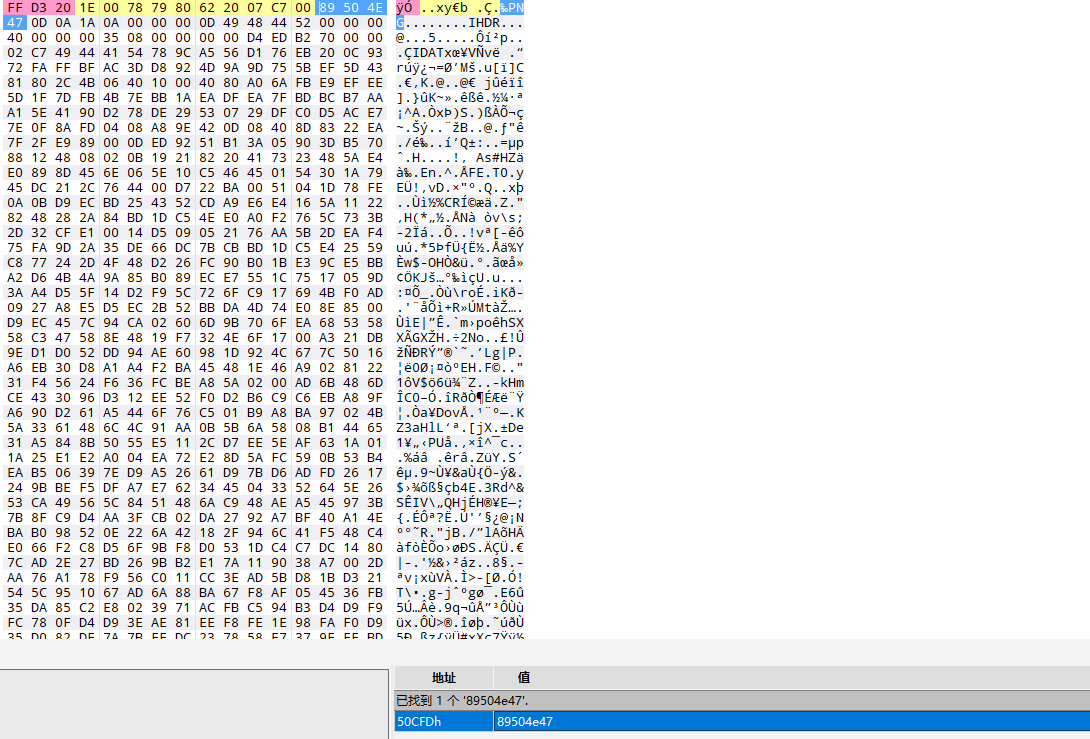
将该png文件复制提取出来，得到cipher_50CFEh_2FEh.png

有点像二维码，甚至Google到了图片降噪

2. 分析png

使用zsteg查看是否存在lsb信息

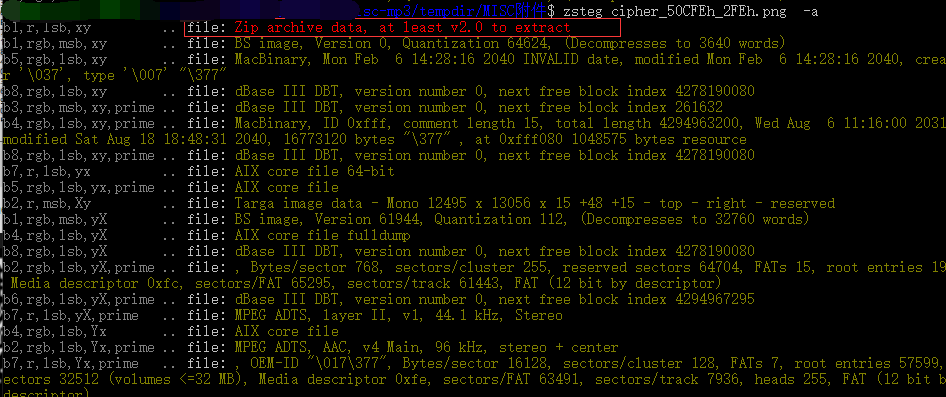
明显看到存在一个zip压缩数据内容。

 zsteg -E 'b1,r,lsb,xy'  cipher_50CFEh_2FEh.png > c1.zip
#该方式提取出来的zip打开会报错，按照zsteg显示的信息使用stegsolve提取一下

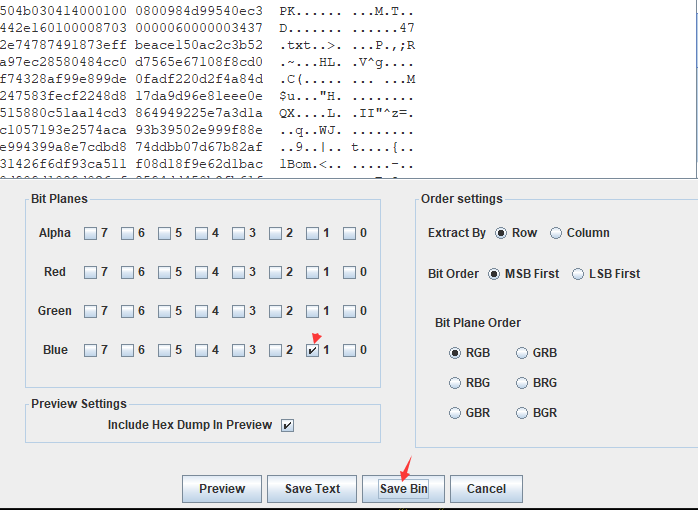
保存后就可以正常打开了，得到一个带密码的压缩包

注：不是伪加密

3.分析zip

密码信息想到一个MP3音频隐写工具  MP3Steno.将cipher.mp3放到工具目录下使用GUI界面解密或者命令行提取都行。

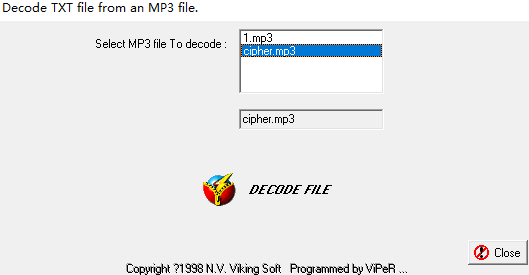
得到

解压成功得到47.txt

4.分析txt

2lO,.j2lL000iZZ2[2222iWP,.ZQQX,2.[002iZZ2[2020iWP,.ZQQX,2.[020iZZ2[2022iWLNZQQX,2.[2202iW2,2.ZQQX,2.[022iZZ2[2220iWPQQZQQX,2.[200iZZ2[202iZZ2[2200iWLNZQQX,2.[220iZZ2[222iZZ2[2000iZZ2[2002iZZ2Nj2]20lW2]20l2ZQQX,2]202.ZW2]02l2]20,2]002.XZW2]22lW2]2ZQQX,2]002.XZWWP2XZQQX,2]022.ZW2]00l2]20,2]220.XZW2]2lWPQQZQQX,2]002.XZW2]0lWPQQZQQX,2]020.XZ2]20,2]202.Z2]00Z2]02Z2]2j2]22l2]2ZWPQQZQQX,2]022.Z2]00Z2]0Z2]2Z2]22j2]2lW2]000X,2]20.,2]20.j2]2W2]2W2]22ZQ-QQZ2]2020ZWP,.ZQQX,2]020.Z2]2220ZQ--QZ2]002Z2]220Z2]020Z2]00ZQW---Q--QZ2]002Z2]000Z2]200ZQ--QZ2]002Z2]000Z2]002ZQ--QZ2]002Z2]020Z2]022ZQ--QZ2]002Z2]000Z2]022ZQ--QZ2]002Z2]020Z2]200ZQ--QZ2]002Z2]000Z2]220ZQLQZ2]2222Z2]2000Z2]000Z2]2002Z2]222Z2]020Z2]202Z2]222Z2]2202Z2]220Z2]2002Z2]2002Z2]2202Z2]222Z2]2222Z2]2202Z2]2022Z2]2020Z2]222Z2]2220Z2]2002Z2]222Z2]2020Z2]002Z2]202Z2]2200Z2]200Z2]2222Z2]2002Z2]200Z2]2022Z2]200ZQN---Q--QZ2]200Z2]000ZQXjQZQ-QQXWXXWXj

　

像是某种编码，通过文件名47，联想到  ROT47

得到另外一串编码，该编码像是js代码变量拼接输出了一些东西，直接F12控制台输出。

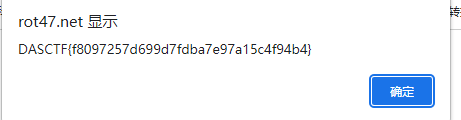
注：希望你能有所收获~~