phpstorm 工具使用技巧(持续补充中。。。)
phpstorm 工具使用技巧(持续补充中。。。)
一、phpstorm大小写切换
1、选择要转换的目标字符串:
//普通商家,普通折扣默认值
'COMMON_DISCOUNT'=>10.00,
'common_settle_discount'=>9.00,
2、然后,按住ctrl+shift+U快捷键,就可实现大小写自动转换
//普通商家,普通折扣默认值
'COMMON_DISCOUNT'=>10.00,
'COMMON_SETTLE_DISCOUNT'=>9.00,
二、phpstorm注释代码
选中要注释的代码,使用快捷键就行了,在phpstorm中快捷键有2种,区别不大
1、ctrl + /,表示 //,即单行注释,即使选择了多行代码,也是多个单行注释
<!--<a href="{:url('product/down',array('id'=>$vo['id']))}"-->
2 <!--class="js-ajax-dialog-btn btn btn-danger"-->
<!--data-msg="确定要下架么">下架</a>-->
2、ctrl + shift + /,表示/**/,即多行注释
<!--<a href="{:url('product/down',array('id'=>$vo['id']))}"
class="js-ajax-dialog-btn btn btn-danger"
data-msg="确定要下架么">下架</a>-->
注意:当注释单行时,两种都可以实现,区别在于使用 ctrl + / 自动注释鼠标定位所在行,不用提前选中注释文本(当然提前选中了更是可以),但是 ctrl + shift + /不行,必须提前选中待注释代码
三、快速折叠与展开
鼠标定位到某处代码之后,可快速折叠或展开最里一层的的代码块,并且由里向外逐步折叠或展开
1、ctrl + - 快速折叠
2、ctrl + + 快速展开
四、代码提示
当不明白某个方法里参数是什么时,可以通过此快捷键得出具体参数列表
1、ctrl+p 代码提示

注意:鼠标一定是定位到方法内部,即括号内
五、自动换行
很多时候代码太长超出了屏幕的宽度,默认情况下没有自动换行的,我们需要把光标往后挪,才能看到后面代码,显得略为蛋疼,我个人比较喜欢能够自动换行。包括书写代码的时候,也是自动换行
1、只对当前文件有效的操作:菜单栏->View -> Active Editor -> Use Soft Wraps;
2、如果想对所有文件都有效,就要在setting里面进行操作:File-> Setting-> Editor-> General -> Use soft wraps in editor。
六、导入和导出配置
导入和导出phpstorm配置信息,
导入:File-->Import Settings
导出:File-->Export Settings
七、更改模板文件
修改phpstorm创建的模板注释
位置:file-->setting-->Editor-->Code style-->File and Code Templates,然后选择Files或include或code,在相应地方添加统一注释即可
比如,我在include下的php function doc comment里,添加这样注释
* des_function:
* author:cyf
* time:${DATE} ${TIME}
,然后在创建function的时候,自动就出来了
八、设置FTP
使用phpstorm做项目的时候,有的时候需要上传ftp,设置ftp比较简单
如图所示: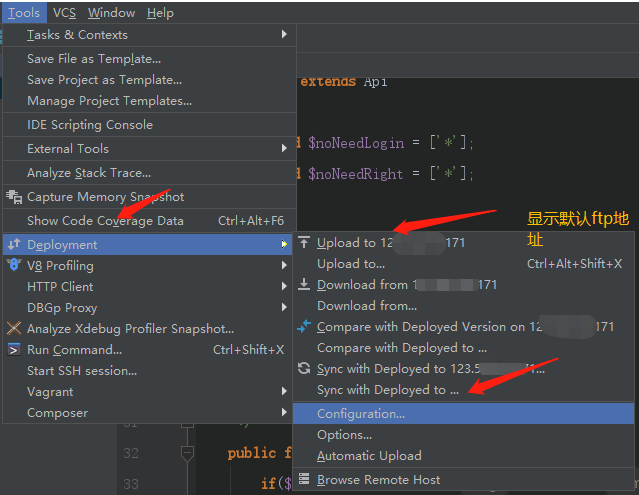

最后,一定不要忘了,设置与服务器相匹配的项目根地址,否则ftp不能使用
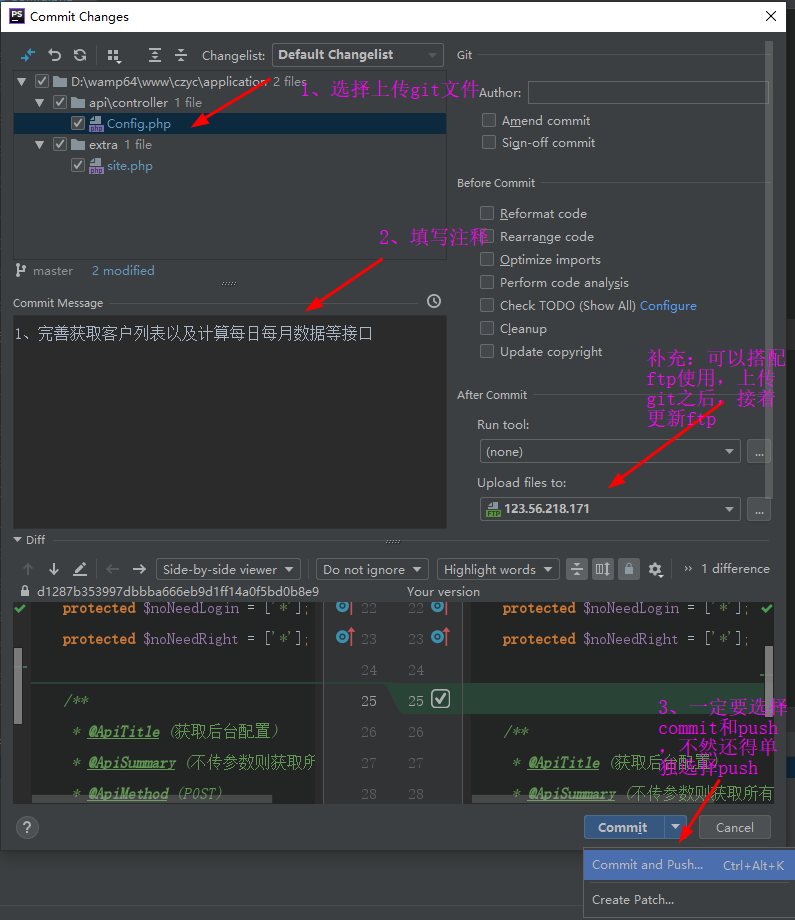
九、设置GIT
设置git比较简单,本地安装完git之后,然后如图所示,操作即可(第一次使用phpstorm设置git的时候,需要设置账户和邮箱)
如图所示: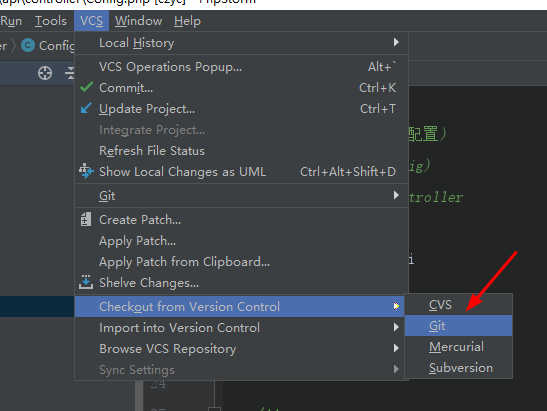 ,
,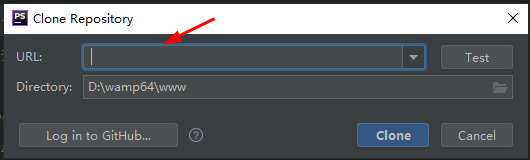
填写完项目源地址之后,就可以clone下来了
如果更改了项目,上传git的时候,操作如图所示
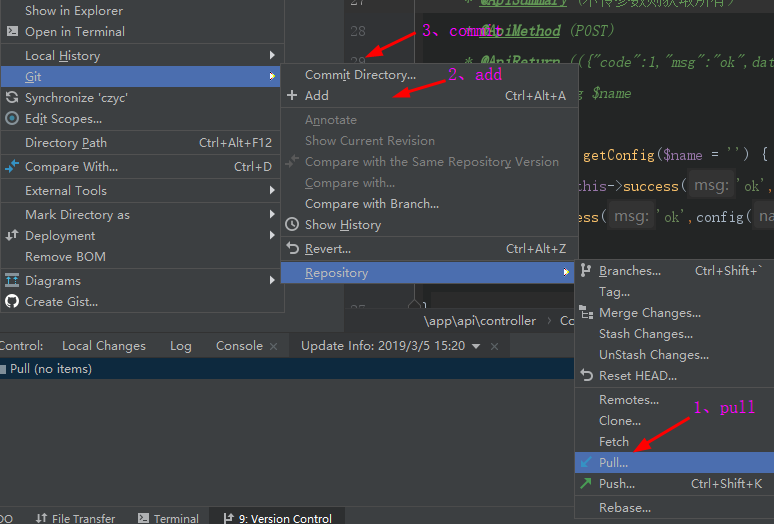
phpstorm 工具使用技巧(持续补充中。。。)的更多相关文章
- fastadmin 后台管理框架使用技巧(持续更新中)
fastadmin 后台管理框架使用技巧(持续更新中) FastAdmin是一款基于ThinkPHP5+Bootstrap的极速后台开发框架,具体介绍,请查看文档,文档地址为:https://doc. ...
- Django-rest-framework(八)使用技巧(持续补充中)
当viewset中,多个action对应了不同的serializers的时候 class UserView(viewsets.GenericViewSet): queryset = User.obje ...
- android开发文档工具集(持续更新中...)
http://www.androiddevtools.cn/ android 产品->交互->视觉->开发->测试各种工具地址下载, 各种文档下载应有尽有,强烈推荐. ht ...
- 来自平时工作中的css知识的积累---持续补充中
① 现代浏览器中,<img>元素默认情况下底部会有空白,那么这个空白到底是从哪里来的? 解惑: method-one:猛戳 来自知乎的解答 method-two: 延伸阅读 what is ...
- Js 过滤emoji表情...持续补充中..
原文来自: https://www.cnblogs.com/tsjTSJ/p/7065544.html 最全最详细的用JS过滤Emoji表情的输入 在前端页面开发过程中,总会碰到不允许输入框输入e ...
- 来自平时工作中的javascript知识的积累---持续补充中
① SeaJs和RequireJS最大的区别 解惑:来自豆友 ② javascript中如何判断undefined var exp = undefined; if (exp === undefined ...
- Android_实验小心得_持续补充中......
1.LineLayout布局控件宽度百分比显示 其中,宽度百分比 = 控件权重 / 所在parent中所有控件权重和 <LinearLayout android:layout_width=&qu ...
- linux常用小技巧(持续更新中)
一.设置固定ip地址1.config查看用的是哪一个网卡这是假设用的是eth12.修改dns地址vim /etc/resolv.confsearch 域名地址nameserver 192.168.3. ...
- vue项目常用方法封装,持续更新中。。。
vue项目中可以直接使用 1.常用工具类untils.js中 /* * 验证手机号是否合格 * true--说明合格 */ export function isPhone(phoneStr){ let ...
随机推荐
- dp优化1——sgq(单调队列)
该文是对dp的提高(并非是dp入门,dp入门者请先参考其他文章) 有时候dp的复杂度也有点大...会被卡. 这几次blog大多数会讲dp优化. 回归noip2017PJT4.(题目可以自己去百度).就 ...
- POJ-2777-CountColor(线段树,位运算)
链接:https://vjudge.net/problem/POJ-2777#author=0 题意: Chosen Problem Solving and Program design as an ...
- Codeforces Round 56-C. Mishka and the Last Exam(思维+贪心)
time limit per test 2 seconds memory limit per test 256 megabytes input standard input output standa ...
- applicationContext中普通数据源不用jndi数据源
applicationContext.xml <?xml version="1.0" encoding="UTF-8"?> <beans xm ...
- BeanCopier使用说明
BeanCopier从名字可以看出了,是一个快捷的bean类复制工具类. 一 如何使用,我就直接丢代码了 public class BeanCopierTest { static SimpleDate ...
- CSS grid layout demo 网格布局实例
直接 上代码,里面我加注释,相当的简单, 也可以去我的github上直接下载代码,顺手给个星:https://github.com/yurizhang/micro-finance-admin-syst ...
- 【Java】JMM内存模型和JVM内存结构
JMM内存模型和JVM内存结构 JAVA内存模型(Java Memory Model) Java内存模型,一般指的是JDK 5 开始使用的新的内存模型,主要由JSR-133: JavaTM Memor ...
- Unity3d通过脚本生成apk
参考链接:http://www.jianshu.com/p/a9261113b4ac 照着链接的方法并没有正确生成APK,IPA没有测试过,不过大致的方法是正确的,修改如下: Environment. ...
- Winform中Checkbox与其他集合列表类型之间进行关联
本文提供了Checkbox与CheckedListBox.DataGridViewCheckBoxColumn等的联动关系 1.CheckboxAssociateFactroy.Create创建联动关 ...
- 用Python完成根据日期计算是星期几
import datetime def week(year,month,day): someday=dayetime.date(year,month,day) result={ "0&quo ...
