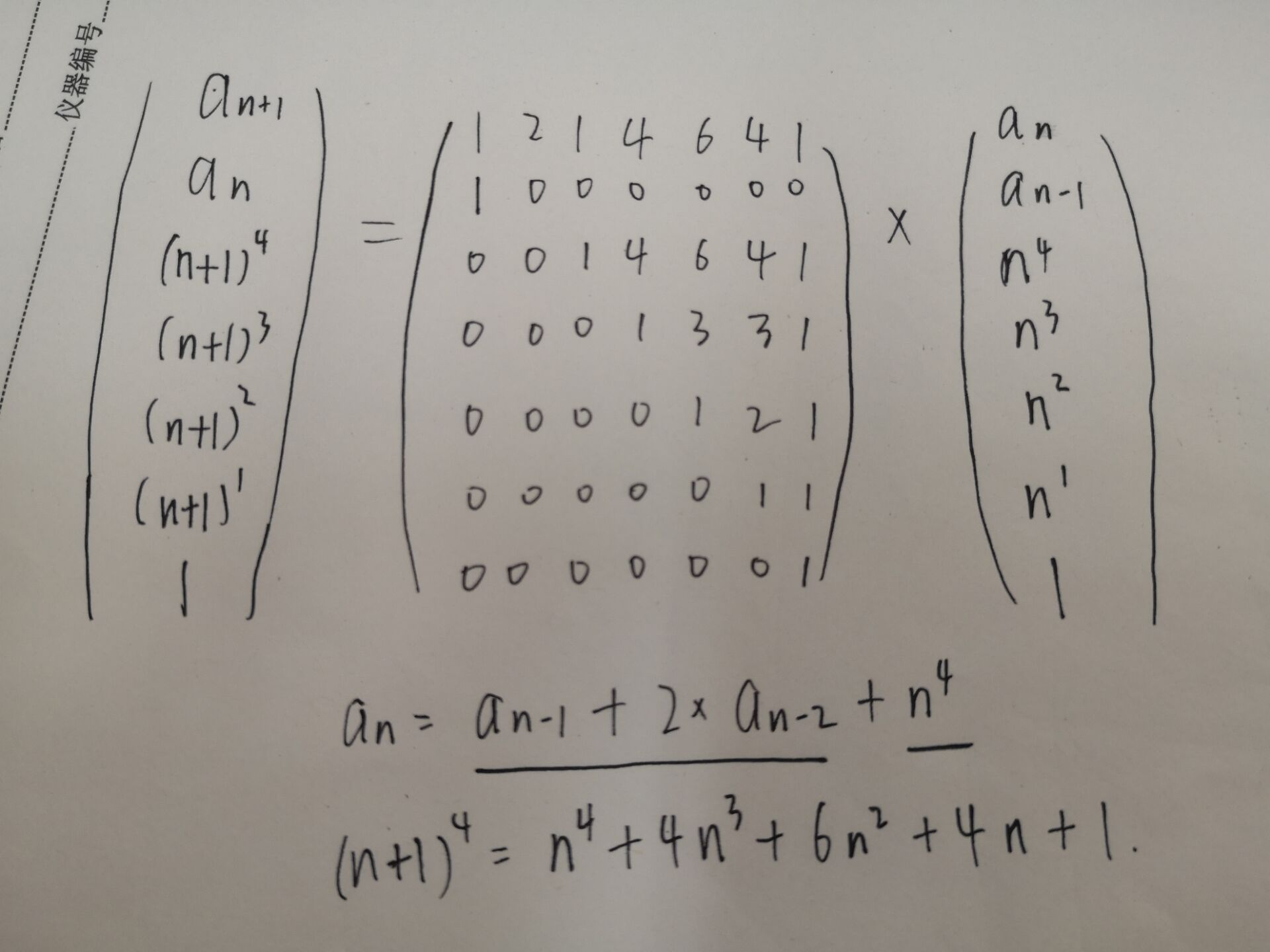HDU - 5950 Recursive sequence(二项式+矩阵合并+矩阵快速幂)
Recursive sequence
InputThe first line of input contains an integer t, the number of test cases. t test cases follow.
Each case contains only one line with three numbers N, a and b where N,a,b < 231231 as described above.
OutputFor each test case, output the number of the N-th cow. This number might be very large, so you need to output it modulo 2147493647.Sample Input
2
3 1 2
4 1 10
Sample Output
85
369
Hint
In the first case, the third number is 85 = 2*1十2十3^4.
In the second case, the third number is 93 = 2*1十1*10十3^4 and the fourth number is 369 = 2 * 10 十 93 十 4^4.
矩阵快速幂。利用了矩阵合并将两个递推关系合并到一个矩阵中。
之前做过了不少含有变量项的题,这道题是底数为变量,指数为常数的一种。
其中变量项的递推利用了二项式定理,系数满足杨辉三角规律。
#include <bits/stdc++.h>
#define MAX 10
#define MOD 2147493647
using namespace std;
typedef long long ll; struct mat{
ll a[MAX][MAX];
}; mat operator *(mat x,mat y)
{
mat ans;
memset(ans.a,,sizeof(ans.a));
for(int i=;i<=;i++){
for(int j=;j<=;j++){
for(int k=;k<=;k++){
ans.a[i][j]+=(x.a[i][k]*y.a[k][j]+MOD)%MOD;
ans.a[i][j]%=MOD;
}
}
}
return ans;
}
mat qMod(mat a,ll n)
{
ll tt[][]={,,,,,,,,
,,,,,,,,
,,,,,,,,
,,,,,,,,
,,,,,,,,
,,,,,,,,
,,,,,,,,
,,,,,,,};
mat t;
for(int i=;i<=;i++){
for(int j=;j<=;j++){
t.a[i][j]=tt[i][j];
}
}
while(n){
if(n&) a=t*a;
n>>=;
t=t*t;
}
return a;
}
int main()
{
int t,i,j;
ll n,a,b;
scanf("%d",&t);
while(t--){
scanf("%I64d%I64d%I64d",&n,&a,&b);
if(n<){
if(n==) printf("%I64d\n",a);
if(n==) printf("%I64d\n",b);
continue;
}
mat x;
memset(x.a,,sizeof(x.a));
x.a[][]=b;
x.a[][]=a;
x.a[][]=***;
x.a[][]=**;
x.a[][]=*;
x.a[][]=;
x.a[][]=;
x=qMod(x,n-);
printf("%I64d\n",x.a[][]);
}
return ;
}
HDU - 5950 Recursive sequence(二项式+矩阵合并+矩阵快速幂)的更多相关文章
- HDU 5950 Recursive sequence 【递推+矩阵快速幂】 (2016ACM/ICPC亚洲区沈阳站)
Recursive sequence Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Other ...
- HDU 5950 Recursive sequence 递推转矩阵
Recursive sequence Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Other ...
- hdu 5950 Recursive sequence 递推式 矩阵快速幂
题目链接 题意 给定\(c_0,c_1,求c_n(c_0,c_1,n\lt 2^{31})\),递推公式为 \[c_i=c_{i-1}+2c_{i-2}+i^4\] 思路 参考 将递推式改写\[\be ...
- HDU 5950 - Recursive sequence - [矩阵快速幂加速递推][2016ACM/ICPC亚洲区沈阳站 Problem C]
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=5950 Farmer John likes to play mathematics games with ...
- HDU 5950 Recursive sequence(矩阵快速幂)
题目链接:Recursive sequence 题意:给出前两项和递推式,求第n项的值. 题解:递推式为:$F[i]=F[i-1]+2*f[i-2]+i^4$ 主要问题是$i^4$处理,容易想到用矩阵 ...
- hdu 5950 Recursive sequence 矩阵快速幂
Recursive sequence Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Other ...
- HDU 5950 Recursive sequence(矩阵快速幂)题解
思路:一开始不会n^4的推导,原来是要找n和n-1的关系,这道题的MOD是long long 的,矩阵具体如下所示 最近自己总是很坑啊,代码都瞎吉坝写,一个long long的输入写成%d一直判我TL ...
- hdu 5950 Recursive sequence
题意:告诉你数列的递推公式为f(n+1)=f(n)+2*f(n-1)+(n+1)^4 以及前两项a,b:问第n项为多少,结果对2147493647取模. 题解:有递推公式,马上应该就能想到矩阵快速幂: ...
- Luogu 3390 【模板】矩阵快速幂 (矩阵乘法,快速幂)
Luogu 3390 [模板]矩阵快速幂 (矩阵乘法,快速幂) Description 给定n*n的矩阵A,求A^k Input 第一行,n,k 第2至n+1行,每行n个数,第i+1行第j个数表示矩阵 ...
随机推荐
- IIS7:通过脚本来配置ftp站点
Appcmd.exe是IIS7提供的一个管理站点的命令行工具,同时支持Ftp和Http的站点,功能还算强大,具体使用方法参考微软网站. 需求 我这里的例子主要配置一个Ftp站点,并且允许CcUser这 ...
- Thinkphp2.2 config.inc.php常用配置
CHECK_FILE_CASE -- windows环境下面的严格检查大小写. /* 项目设定 */ 'APP_DEBUG' => false, // 是否开启调试模式 'AP ...
- matlab使用usb和gige 网口相机
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 辛苦原创所得,转载请注明出处 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% ...
- event loop笔记
注意四个对象: 主进程 执行栈 异步进程 任务队列 1.主进程读取js代码,形成对应的堆和执行栈(此时在同步环境) 2.当遇见异步任务,转交给异步进程进行处理 3.异步任务完成,将其推入任务队列 4. ...
- POJ3415 Common Substrings —— 后缀数组 + 单调栈 公共子串个数
题目链接:https://vjudge.net/problem/POJ-3415 Common Substrings Time Limit: 5000MS Memory Limit: 65536K ...
- Protothread 机制
一.概述 很多传感器操作系统都是基于事件驱动模型的,事件驱动模型不用为每个进程都分配一个进程栈,这对内存资源受限的无线传感器网络嵌入式系统尤为重要. 然而事件驱动模型不支持阻塞等待抽象语句,因此程序员 ...
- JQuery调用iframe子页面函数/对象的方法
父页面有个ID为mainfrm的iframe,iframe连接b.html,该页面有个函数test 在父页面调用b.html的test方法为: $("#mainfrm")[0].c ...
- listen 69
Today Is Unlucky for People Who Have Bad Luck Today If you have Paraskevidekatriaphobia, today is no ...
- 第十五章-Web开发
随着web的发展, 最开始使用的CS架构已经不适合web了, 现在web使用的架构是BS架构 如今大部分重量级的软件都以web形式提供了 web开发的四个阶段 1) 静态web页面 2) CGI: 静 ...
- HihoCoder1677 : 翻转字符串(Splay)(区间翻转)
描述 给定一个字符串S,小Hi希望对S进行K次翻转操作. 每次翻转小Hi会指定两个整数Li和Ri,表示要将S[Li..Ri]进行翻转.(S下标从0开始,即S[0]是第一个字母) 例如对于S=" ...