棋盘覆盖问题 （粉书 P230 【递归】** ）

转载自：http://blog.csdn.net/akof1314/article/details/5423608  （赞）

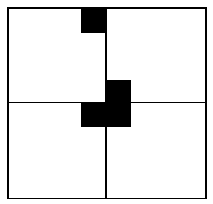
在一个 2^k * 2^k 个方格组成的棋盘中，若恰有一个方格与其它方格不同，则称该方格为一特殊方格，称该棋盘为一特殊棋盘。显然特殊方格在棋盘上出现的位置有 4^k 种情形。因而对任何 k>=0 ，有 4^k 种不同的特殊棋盘。下图所示的特殊棋盘为 k=2 时 16 个特殊棋盘中的一个。

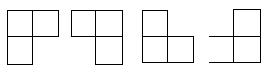
在棋盘覆盖问题中，要用下图中 4 中不同形态的 L 型骨牌覆盖一个给定的特殊棋牌上除特殊方格以外的所有方格，且任何 2 个 L 型骨牌不得重叠覆盖。易知，在任何一个 2^k * 2^k 的棋盘中，用到的 L 型骨牌个数恰为 (4^k-1)/3 。

用分治策略，可以设计解棋盘问题的一个简捷的算法。
当 k>0 时，将 2^k * 2^k 棋盘分割为 4 个 2^(k-1) * 2^(k-1) 子棋盘，如下图所示。

特殊方格必位于 4 个较小子棋盘之一中，其余 3 个子棋盘中无特殊方格。为了将这 3 个无特殊方格的子棋盘转化为特殊棋盘，我们可以用一个 L
型骨牌覆盖这 3 个较小的棋盘的汇合处，如下图所示，这 3 个子棋盘上被 L 型骨牌覆盖的方格就成为该棋盘上的特殊方格，从而将原问题化为 4
个较小规模的棋盘覆盖问题。递归的使用 这种分割，直至棋盘简化为 1x1 棋盘。

对于上面图一的示例，棋盘覆盖效果如下：

c++d代码如下：

    #include<iostream>
    using namespace std;
    int tile=1;                   //L型骨牌的编号(递增)
    int board[100][100];  //棋盘
    /*****************************************************
    * 递归方式实现棋盘覆盖算法
    * 输入参数：
    * tr--当前棋盘左上角的行号
    * tc--当前棋盘左上角的列号
    * dr--当前特殊方格所在的行号
    * dc--当前特殊方格所在的列号
    * size：当前棋盘的:2^k
    *****************************************************/
    void chessBoard ( int tr, int tc, int dr, int dc, int size )
    {
        if ( size==1 )    //棋盘方格大小为1,说明递归到最里层
            return;
        int t=tile++;     //每次递增1
        int s=size/2;    //棋盘中间的行、列号(相等的)
        //检查特殊方块是否在左上角子棋盘中
        if ( dr<tr+s && dc<tc+s )              //在
            chessBoard ( tr, tc, dr, dc, s );
        else         //不在，将该子棋盘右下角的方块视为特殊方块
        {
            board[tr+s-1][tc+s-1]=t;
            chessBoard ( tr, tc, tr+s-1, tc+s-1, s );
        }
        //检查特殊方块是否在右上角子棋盘中
        if ( dr<tr+s && dc>=tc+s )               //在
            chessBoard ( tr, tc+s, dr, dc, s );
        else          //不在，将该子棋盘左下角的方块视为特殊方块
        {
            board[tr+s-1][tc+s]=t;
            chessBoard ( tr, tc+s, tr+s-1, tc+s, s );
        }
        //检查特殊方块是否在左下角子棋盘中
        if ( dr>=tr+s && dc<tc+s )              //在
            chessBoard ( tr+s, tc, dr, dc, s );
        else            //不在，将该子棋盘右上角的方块视为特殊方块
        {
            board[tr+s][tc+s-1]=t;
            chessBoard ( tr+s, tc, tr+s, tc+s-1, s );
        }
        //检查特殊方块是否在右下角子棋盘中
        if ( dr>=tr+s && dc>=tc+s )                //在
            chessBoard ( tr+s, tc+s, dr, dc, s );
        else         //不在，将该子棋盘左上角的方块视为特殊方块
        {
            board[tr+s][tc+s]=t;
            chessBoard ( tr+s, tc+s, tr+s, tc+s, s );
        }
    }  

    void main()
    {
        int size;
        cout<<"输入棋盘的size(大小必须是2的n次幂): ";
        cin>>size;
        int index_x,index_y;
        cout<<"输入特殊方格位置的坐标: ";
        cin>>index_x>>index_y;
        chessBoard ( 0,0,index_x,index_y,size );
        for ( int i=0; i<size; i++ )
        {
            for ( int j=0; j<size; j++ )
                cout<<board[i][j]<<"/t";
            cout<<endl;
        }
    }

参考文献：

1.       《算法设计与分析》 --------------------------  王红梅编著   清华大学出版社
2.      
棋盘覆盖算法                                  
http://riddickbryant.javaeye.com/blog/559388
3.       棋盘覆盖问题原理及演示程序                     http://www.cnblogs.com/lsxqw2004/archive/2008/10/16/1313086.html