LOJ N！在不同进制的位数

lightoj1045 - Digits of Factorial (N！不同进制的位数)

对于一个B进制的数，只需要对其取以B的对数就可以得到他在B进制情况下的位数(取了对数之后可能为小数，所以还需要取整后再+1)

—  N ! 的位数就是  [lg(N!)]+1=[lg(1)+lg(2)+…+lg(N)]+1

—= (int) ceil[(n*ln(n)-n+0.5*ln(2*n*π))/ln(10)]      /*ceil是向上取整,[]符号为取整*/

—   最后一个式子被称为斯特林公式

 

 

 

cin>>n;
cout<<(int)(ceil((n*log(n)-n+0.5*log(*n*pi))/log()))<<endl;

---

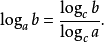【换底公式：logx (n!) = log(n!) /  log(x) 】

  【阶乘变加法：log (n!)=log1 + log2 + log3 + log4 +……+log(n),】

 

N !在10进制下的位数为log10 (n!) + 1;  所以在x进制下的位数为logx (n!) + 1;

但是计算机只能表示以10和e为底的对数，所以要用换底公式，logx (n!) = log(n!) /  log(x) ;【注意，等号右边的 log 都是默认以e为底】

log (n!)=log1 + log2 + log3 + log4 +……+log(n), 所以n比较大时计算log(n!)时已经把其他数的阶乘也算出来了，

如果给出一个n都要计算阶乘的话，费时间o(n),所以可以把 log (n!) 先用double型数组sum[]先存起来，令sun[i]=log(i!)

先预处理出sum[i]后面可直接调用；

#include<stdio.h>
#include<string.h>
#include<math.h>
double sum[];//数组要是double型的；
int main()
{
    memset(sum,,sizeof(sum));
    sum[]=log();
    for(int i=;i<=;i++)
    {
        sum[i]=sum[i-]+log(i);
    }
    int t,n,b,mm=;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d%d",&n,&b);
        if(n==)
        {
            printf("Case %d: 1\n",mm++);//0的阶乘等于1，此时不能用sum[0],因为真数不能为0不符合所以要单独列出；
        }
        else
        {
            int c;//定义一个整形c,把double强制转换成int ;
            c=sum[n]/log(b)+;
            printf("Case %d: %d\n",mm++,c);
        }
    }
    return ;
}