面向对象OONo.3单元总结

一，JML语言

　　1）JML理论基础：JML是一类语言，用来描述一个方法或一个类的功能、以及这个类在实现这个功能时需要的条件、可能改变的全局变量、以及由于条件问题不能实现功能时这个方法或类的行为，具有明了、描述清晰的特点

　　　　　　　　　　最主要的词语有：

　　　　　　　　　　　　　　　　　　require：描述达到功能所需要的条件

　　　　　　　　　　　　　　　　　　ensures：描述不同的条件会产生什么结果

　　　　　　　　　　　　　　　　　　assignable：描述有哪些全局变量会被改变

　　　　　　　　　　专有名词会用“\XX”形式，如“最大”会用"\max"

　　　　　　　　　　写的时候跟着一些例子写就行了，一个小例子：

　　

　　　　　　　　　　

　　2）应用工具链

　　　　　　　　　openjml:用来检查方法前的JML描述是否有错误，类似于检查代码的语法

　　　　　　　　　Junit:可根据方法前的JML描述自动生成自动测试框架

二，JMLUnit的使用

　　很遗憾最后一步没能成功，不过下面有一些过程的截图

　　

　　1）源程序

　　

　　2）使用命令 javac -jar jmlunitng.jar */java自动生成的

　　

　　　　3）不过生成的里面都显示红色就很迷，导入jmlunitng.jar包也不行，don't know y,可能必须要外带.jar文件用命令行运行吧　　　　

　　

　　4）最迷的可能是这个了，no matter what

　　

三，架构设计

　　1）第三次作业的要求是实现无向图地铁，要求实现的方法主要有：两节点间最短路径、两节点之间最少换乘、两节点之间最少车费、两节点间最少不满意度

　　2）我的架构：

　　　　　　a)节点的映射：　由于最多120个不同的节点

　　　　　　　　MyPath：节点->一个HashMap中的位置posi1，0<=posi<119

　　　　　　　　MyRailwayStation:节点->一个HashMap中的位置posi2，0<=posi2<119

　　　　　　　　一个节点在它所在的path中的位置posi1都是不同的，而其在Graph中的posi2绝对是不变的——除非这个点被删掉了

　　　　　　b)MyGraph中主要的容器：

　　　　　　　　　　　　　　　　　a)　 HashMap<Integer,Hashmap<Integer>> shortest（最短路径），里面的hashmap存的是与 posi2=integer的节点 的所有有边或都在一条路径中的点与posi2的最短距离

　　　　　　　　　　　　　　　　　　同上，还有least_money（最少路费）,least_unpleasant（最少不满意度）

　　　　　　　　　　　　　　　　　b) HashMap<Integer,Hashmap<Integer>> firsty（最短路径）：里面存所有点与posi2=integer的点的最短路线——因为用的迪杰斯特拉算法，算一次其它所有点与这个点的最短路径就得出来了。

　　　　　　　　　　　　　　　　　　同上，还有 secondy（最少路费）、thirdy（最少不满意度）

　　　　　　c)各类中主要的方法：

　　　　　　　　MyPath:

　　　　　　　　　　　　get_shortest_path_length(node1,node2):用以计算仅在这条path中，node1到node2之间的最短距离

　　　　　　　　　　　　get_least_unpleasant（node1,node2）同上

　　　　　　　　Mygraph:

　　　　　　　　　　　　Fresh(MyPath path):调用MyPath中的get_shortest_path_length(node1,node2)……得到一条path中所有点之间的最短路径、最少不满意度，更新shortest、least_money、least_unpleasant中（比原来的小就更新，不小就不更新）

　　　　　　　　　　　　Get_shortest_path_length(node1,node2):利用迪杰斯特拉算法，利用shortest中的数据，得到最短路径

　　　　　　　　　　　　Get_least_unpleasant:同上，利用least_unpleasant中的数据

　　　　　　　　　　　　Get_least_money:同上，利用least_money中的数据

　　　　　　　　　　　　Path_add:每加一条新的路径，现调用fresh ,更新shortest、least_money、least_unpleasant，但清空first、secondy、thirdy，以后再要找最短路径又要重新经过一遍迪杰斯特拉

　　　　　　　　　　　　Path_remove:

　　　　　　　　　　　　　　　　　　a)每删一条路径，清空所有shortest、least_money、least_unpleasant、first、secondy、thirdy

　　　　　　　　　　　　　　　　　　b)将剩下的所有path逐个调用Fresh(MyPath path)函数，重新生成shortest、least_money、least_unpleasant

　　　　　　　　Follow:封装所有节点的  与其它所有点的最短路径、最少路费、最少不满意度

　　　　　　*d)一定程度的封装：

　　　　　　　　　　作业3几乎重构于作业2:，一方面是因为两者的要求变了：作业3除了最短路径还有x+2y这样的“令人模棱两可的选择取值”的计算（即可能x大y小，与 x小y大有一样的结果）；另一方面是作业3不仅只有一个图，为了方便计算还应自己将同类数据抽出来形成新的图——如firsty一个图，secondy一个图……

　　　　　　　　　　所以我选择重构+封装：

　　　　　　　　　　　　用 firsty 构造图，边权值为两点间的最短路径，用second、third……

　　　　　　　　　　　　用Follow类封装各个节点的与其它所有点的最短路径等，Follow类包括修改和存储两种功能

　　　　　　　　　　　　Graph类中将本来四个迪杰斯特拉算法的方法（最短路径、最少路费、最少不满意度、最少换乘）整合为一个迪杰斯特拉算法，用数字 1,2,3,4 标记其是算最短路径还是算最少路费等什么的——主要是来区分从哪个容器中取数据

　　　　　　*e)算法：

　　　　　　　　　　我这次用的是讨论区中大佬的算法，因为有换乘，所以先将各个path中个点之间的“最短XX”都算出来，如最少换乘，就设一条path中各个点之间的“距离”都为1,然后换乘时就能自动+1表示换乘了另外一条路径，最少路费(2y+x:y为换乘次数，x为经过的站点的个数)就设一条path中任意两点的距离为 其在这条path中的最短路径+2，这样就还是当“最短路径”算，而每次path之间换乘时，“2y”实际就已经加上去了，只是最后会多2，要剪掉

　　3）类图和一些数据：

　　

　　　　　　　　

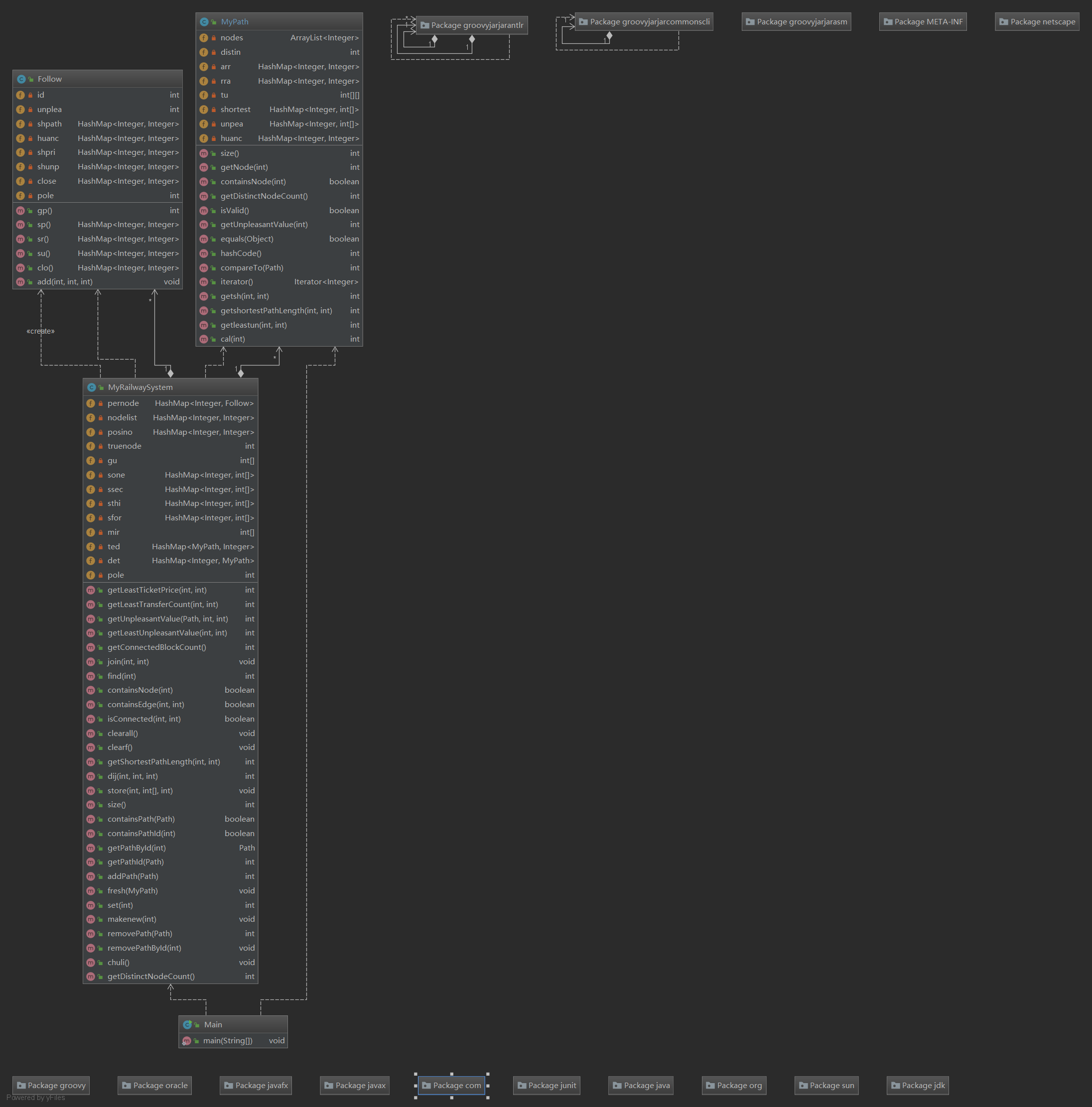
四，bug与修复

　　　　　　我自己被检查出的bug；

　　　　　　　　　　第一次：因为算法问题，一个方法中出现了死循环

　　　　　　　　　　第二次：因为容器过多而在更改架构时没去清理，有的地方判断条件也没改，导致“过气的判断条件扼住了命运的喉咙”……我是出了结果才恍然发现哪里哪里错了

　　　　　　　　　　第三次：我第三次作业虽然这样的实现方法容易TLE或“cpu”，但我最大的问题是映射关系混乱：MyPath类中节点对应的posi1易混在MyGraph类中用了、将节点对应的posi2混成了节点的数值……终归是我刚开始时构思不到位，结果写的时候就这里堆一点、那里堆一点，整个联系起来时就乱了套，结果是强测炸掉……

　　　　　　我找别人的bug:

　　　　　　　　　　第一次：由于时间的要求很高，因为他们和我一样在（get_distinct_node）方法中循环整个Container,而不是将其分散到Container发生变动（add_path/remove_path）时，所以只从这一个地方hack了。

　　　　　　　　　　第二次：自己做了简易的对拍器，控制各种指令的数量，不过最终，由于room内他们用的是弗洛伊德算法，也没有保存查询结果，所以平均算法复杂度非常高，我利用“超时”这一点（不断地get_shortest_path(node1,node2)）hack到了一些点

　　　　　　　　　　

五，心得体会

　　　　　　（1）利用JML这种契约式语言的工程很简洁利落，逻辑分明:

　　　　　　　　　　JML只需要描述有哪些方法及这些方法的条件、目的、变动了什么——然后，“怎样实现”全部交给你。乍一看，跟着各个方法前的JML的描述来写就行了，但实际上，还需要将所有方法拉到一起，分析需要哪些容器、变量，甚至一些方法之间是互相影响的，所以又要选择什么样的算法——比如我如果使用“枚举x,y来得到最小x+2y”的方法，我的时间复杂度就完了——超高。最后最好再封装一下。

　　　　　　　　　　实现的过程纠结挣扎，但写完代码后校对程序是否满足需求会非常简单，因为JML描述得简洁明了，且逻辑分明、无二义性。而且因为JML描述得很明了，虽然思考过程可能会有点长，但思路是不会偏的。

　　　　　　（2）正因为（1），所以自己写JML规格描述时要仔细琢磨：是否涵盖了所有情况？描述的是否清晰？描述的是否正确？有较大的挑战。