Red Black Tree 红黑树 AVL trees 2-3 trees 2-3-4 trees B-trees Red-black trees Balanced search tree 平衡搜索树

小结：

1、红黑树：典型的用途是实现关联数组

2、旋转

当我们在对红黑树进行插入和删除等操作时，对树做了修改，那么可能会违背红黑树的性质。
为了保持红黑树的性质，我们可以通过对树进行旋转，即修改树中某些结点的颜色及指针结构，以达到对红黑树进行插入、删除结点等操作时，红黑树依然能保持它特有的性质（五点性质）。

https://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-046j-introduction-to-algorithms-sma-5503-fall-2005/video-lectures/lecture-10-red-black-trees-rotations-insertions-deletions/lec10.pdf

Balanced search trees Balanced search tree: A search-tree data structure for which a height of O(lg n) is guaranteed when implementing a dynamic set of n items.

AVL trees

2-3 trees

2-3-4 trees

B-trees

Red-black trees

【1】

Example of a red-black tree

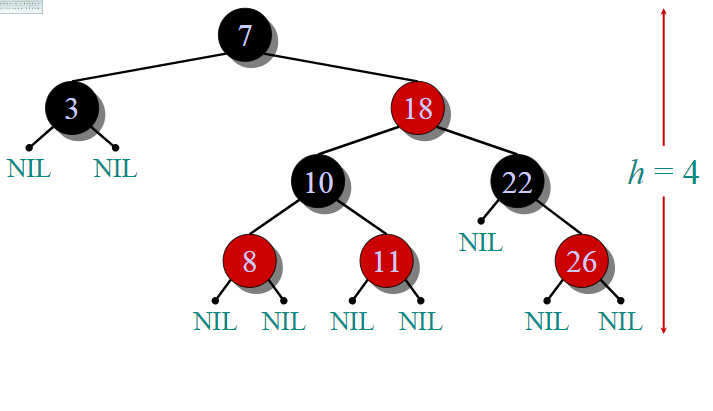
This data structure requires an extra one-bit color field in each node.
Red-black properties:
1. Every node is either red or black.
2. The root and leaves (NIL’s) are black.
3. If a node is red, then its parent is black.
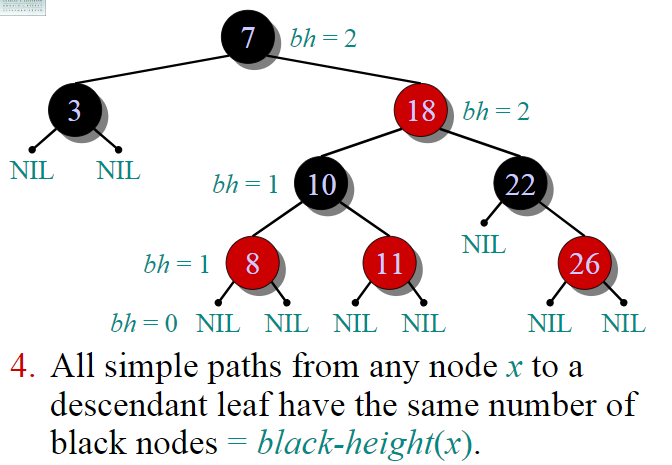
4. All simple paths from any node x to a descendant leaf have the same number of black nodes = black-height(x).

红黑树是每个节点都带有颜色属性的二叉查找树，颜色或红色或黑色。在二叉查找树强制一般要求以外，对于任何有效的红黑树我们增加了如下的额外要求:

性质1. 节点是红色或黑色。

性质2. 根节点是黑色。

性质3 每个叶节点（NIL节点，空节点）是黑色的。

性质4 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)

性质5. 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点

http://pages.cs.wisc.edu/~skrentny/cs367-common/readings/Red-Black-Trees/index.html

Recall that, for binary search trees, although the average-case times for the lookup, insert, and delete methods are all O(log N), where N is the number of nodes in the tree, the worst-case time is O(N). We can guarantee O(log N) time for all three methods by using a balanced tree -- a tree that always has height O(log N)-- instead of a binary search tree.

A number of different balanced trees have been defined, including AVL trees, 2-4 trees, and B trees. You might learn about the first two in an algorithms class and the third in a database class. Here we will look at yet another kind of balanced tree called a red-black tree.

The important idea behind all of these trees is that the insert and delete operations may restructure the tree to keep it balanced. So lookup, insert, and delete will always be logarithmic in the number of nodes but insert and delete may be more complicated than for binary search trees.

A red-black tree is a binary search tree in which

each node has a color (red or black) associated with it (in addition to its key and left and right children)
the following 3 properties hold:
1. (root property) The root of the red-black tree is black
2. (red property) The children of a red node are black.
3. (black property) For each node with at least one null child, the number of black nodes on the path from the root to the null child is the same.

An example of a red-black tree is shown below:

https://baike.baidu.com/item/红黑树

红黑树（Red Black Tree）是一种自平衡二叉查找树，是在计算机科学中用到的一种数据结构，典型的用途是实现关联数组。

它是在1972年由Rudolf Bayer发明的，当时被称为平衡二叉B树（symmetric binary B-trees）。后来，在1978年被 Leo J. Guibas 和 Robert Sedgewick 修改为如今的“红黑树”。

红黑树和AVL树类似，都是在进行插入和删除操作时通过特定操作保持二叉查找树的平衡，从而获得较高的查找性能。

它虽然是复杂的，但它的最坏情况运行时间也是非常良好的，并且在实践中是高效的：它可以在O(log n)时间内做查找，插入和删除，这里的n 是树中元素的数目。

中文名: 红黑树
外文名: RED-BLACK-TREE
性质: 自平衡二叉查找树

用途: 实现关联数组
发明人: 鲁道夫·贝尔
发明时间: 1972年
别名: 对称二叉B树

数据结构

它的统计性能要好于平衡二叉树(有些书籍根

红黑树

据作者姓名，Adelson-Velskii和Landis，将其称为AVL-树)，因此，红黑树在很多地方都有应用。在C++ STL中，很多部分(包括set, multiset, map, multimap)应用了红黑树的变体(SGI STL中的红黑树有一些变化，这些修改提供了更好的性能，以及对set操作的支持)。其他平衡树还有：AVL，SBT，伸展树，TREAP 等等。

树的旋转

当我们在对红黑树进行插入和删除等操作时，对树做了修改，那么可能会违背红黑树的性
质。

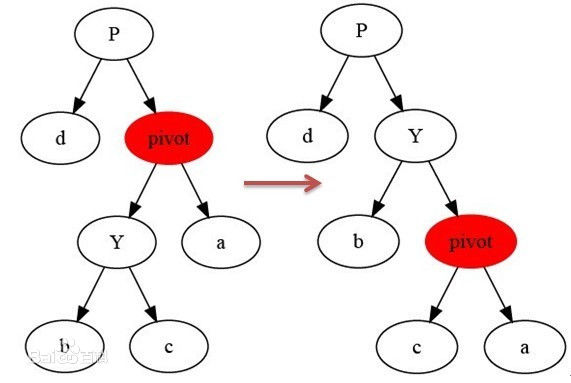
树的左旋

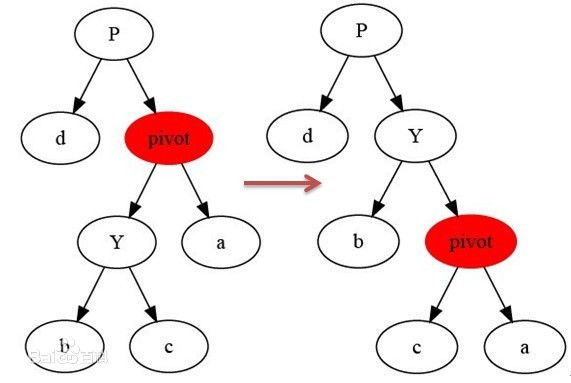
树的右旋

为了保持红黑树的性质，我们可以通过对树进行旋转，即修改树中某些结点的颜色及指针结构，以达到对红黑树进行插入、删除结点等操作时，红黑树依然能保持它特有的性质（五点性质）。

如右图。

性质

性质1. 节点是红色或黑色。

性质2. 根节点是黑色。

性质3 每个叶节点（NIL节点，空节点）是黑色的。

性质4 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)

性质5. 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。

这些约束强制了红黑树的关键性质: 从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。结果是这个树大致上是平衡的。因为操作比如插入、删除和查找某个值的最坏情况时间都要求与树的高度成比例，这个在高度上的理论上限允许红黑树在最坏情况下都是高效的，而不同于普通的二叉查找树。

要知道为什么这些特性确保了这个结果，注意到性质4导致了路径不能有两个毗连的红色节点就足够了。最短的可能路径都是黑色节点，最长的可能路径有交替的红色和黑色节点。因为根据性质5所有最长的路径都有相同数目的黑色节点，这就表明了没有路径能多于任何其他路径的两倍长。

在很多树数据结构的表示中，一个节点有可能只有一个子节点，而叶子节点不包含数据。用这种范例表示红黑树是可能的，但是这会改变一些属性并使算法复杂。为此，本文中我们使用 "nil 叶子" 或"空(null)叶子"，如上图所示，它不包含数据而只充当树在此结束的指示。这些节点在绘图中经常被省略，导致了这些树好象同上述原则相矛盾，而实际上不是这样。与此有关的结论是所有节点都有两个子节点，尽管其中的一个或两个可能是空叶子。

术语

红黑树是一种特定类型的二叉树，它是在计算机科学中用来组织数据比如数字的块的一种结构。所有数据块都存储在节点中。这些节点中的某一个节点总是担当起始位置的功能，它不是任何节点的儿子，我们称之为根节点或根。它有最多两个"儿子"，都是它连接到的其他节点。所有这些儿子都可以有自己的儿子，以此类推。这样根节点就有了把它连接到在树中任何其他节点的路径。

如果一个节点没有儿子，我们称之为叶子节点，因为在直觉上它是在树的边缘上。子树是从特定节点可以延伸到的树的某一部分，其自身被当作一个树。在红黑树中，叶子被假定为 null 或空。

由于红黑树也是二叉查找树，它们当中每一个节点的比较值都必须大于或等于在它的左子树中的所有节点，并且小于或等于在它的右子树中的所有节点。这确保红黑树运作时能够快速的在树中查找给定的值。

用途

红黑树和AVL树一样都对插入时间、删除时间和查找时间提供了最好可能的最坏情况担保。这不只是使它们在时间敏感的应用如即时应用(real time application)中有价值，而且使它们有在提供最坏情况担保的其他数据结构中作为建造板块的价值；例如，在计算几何中使用的很多数据结构都可以基于红黑树。

红黑树在函数式编程中也特别有用，在这里它们是最常用的持久数据结构之一，它们用来构造关联数组和集合，在突变之后它们能保持为以前的版本。除了O(log n)的时间之外，红黑树的持久版本对每次插入或删除需要O(log n)的空间。

红黑树是 2-3-4树的一种等同。换句话说，对于每个 2-3-4 树，都存在至少一个数据元素是同样次序的红黑树。在 2-3-4 树上的插入和删除操作也等同于在红黑树中颜色翻转和旋转。这使得 2-3-4 树成为理解红黑树背后的逻辑的重要工具，这也是很多介绍算法的教科书在红黑树之前介绍 2-3-4 树的原因，尽管 2-3-4 树在实践中不经常使用。

操作

在红黑树上只读操作不需要对用于二叉查找树的操作做出修改，因为它也是二叉查找树。但是，在插入和删除之后，红黑属性可能变得违规。恢复红黑属性需要少量(O(log n))的颜色变更(这在实践中是非常快速的)并且不超过三次树旋转(对于插入是两次)。这允许插入和删除保持为 O(log n) 次，但是它导致了非常复杂的操作。