Xor-sequences CodeForces - 691E || 矩阵快速幂

Xor-sequences CodeForces - 691E

题意：在有n个数的数列中选k个数（可以重复选，可以不按顺序）形成一个数列，使得任意相邻两个数异或的结果转换成二进制后其中1的个数是三的倍数。求可能形成的不同数列个数（只要选出的数列中，任意两个元素在原序列中的位置不同，就算作不同的序列，比如在原数列[1,1]中选1个，那么第一个1和第二个1要分开算）。

方法：

很容易列出dp方程：

dp[k][i]表示取了k个，最后一个在第i位。a[i][j]表示i和j异或结果转换成二进制后1的个数是否是3的倍数，1表示是，0表示否。

$dp[k][i]=dp[k-1][1]*a[1][i]+...dp[k-1][n]*a[n][i]$

注意，不是$dp[k][i]=dp[k-1][1]*a[1][i]+...+dp[k-1][i-1]*a[i-1][i]$（这道题是可以重复、不按顺序选的，这么写就是不重复、按顺序）

那么，这样的算法复杂度就是O(nk)，太慢了，需要优化。

从小数据开始：

n=3时：

dp[1][1]=1
dp[1][2]=1
dp[1][3]=1

dp[2][1]=dp[1][1]*a[1][1]+dp[1][2]*a[2][1]+dp[1][3]*a[3][1]
dp[2][2]=dp[1][1]*a[1][2]+dp[1][2]*a[2][2]+dp[1][3]*a[3][2]
dp[2][3]=dp[1][1]*a[1][3]+dp[1][2]*a[2][3]+dp[1][3]*a[3][3]

dp[3][1]=dp[2][1]*a[1][1]+dp[2][2]*a[2][1]+dp[2][3]*a[3][1]
dp[3][2]=dp[2][1]*a[1][2]+dp[2][2]*a[2][2]+dp[2][3]*a[3][2]
dp[3][3]=dp[2][1]*a[1][3]+dp[2][2]*a[2][3]+dp[2][3]*a[3][3]

很容易可以发现：
矩阵1
dp[1][1] dp[1][2] dp[1][3]
矩阵2
 a[1][1]  a[1][2]  a[1][3]
 a[2][1]  a[2][2]  a[2][3]
 a[3][1]  a[3][2]  a[3][3]
矩阵1*矩阵2
dp[2][1] dp[2][2] dp[2][3]

更大的数据以此类推，因此很容易想到用矩阵快速幂优化。

而要求dp[k][]，就要由dp[1][]乘k-1次矩阵2，可以改为算出来矩阵2的k-1次幂放入矩阵3，再将dp[1][]乘上矩阵3，得到的就是dp[k][]。最终答案就是dp[k][1]+..+dp[k][n]。

所以说...这个矩阵快速幂的题..居然不用自己去构造转移矩阵??

另外：

__builtin_popcountll：参照__builtin_popcount，那个是针对long整型的，这个是针对long long的

还有手动写的

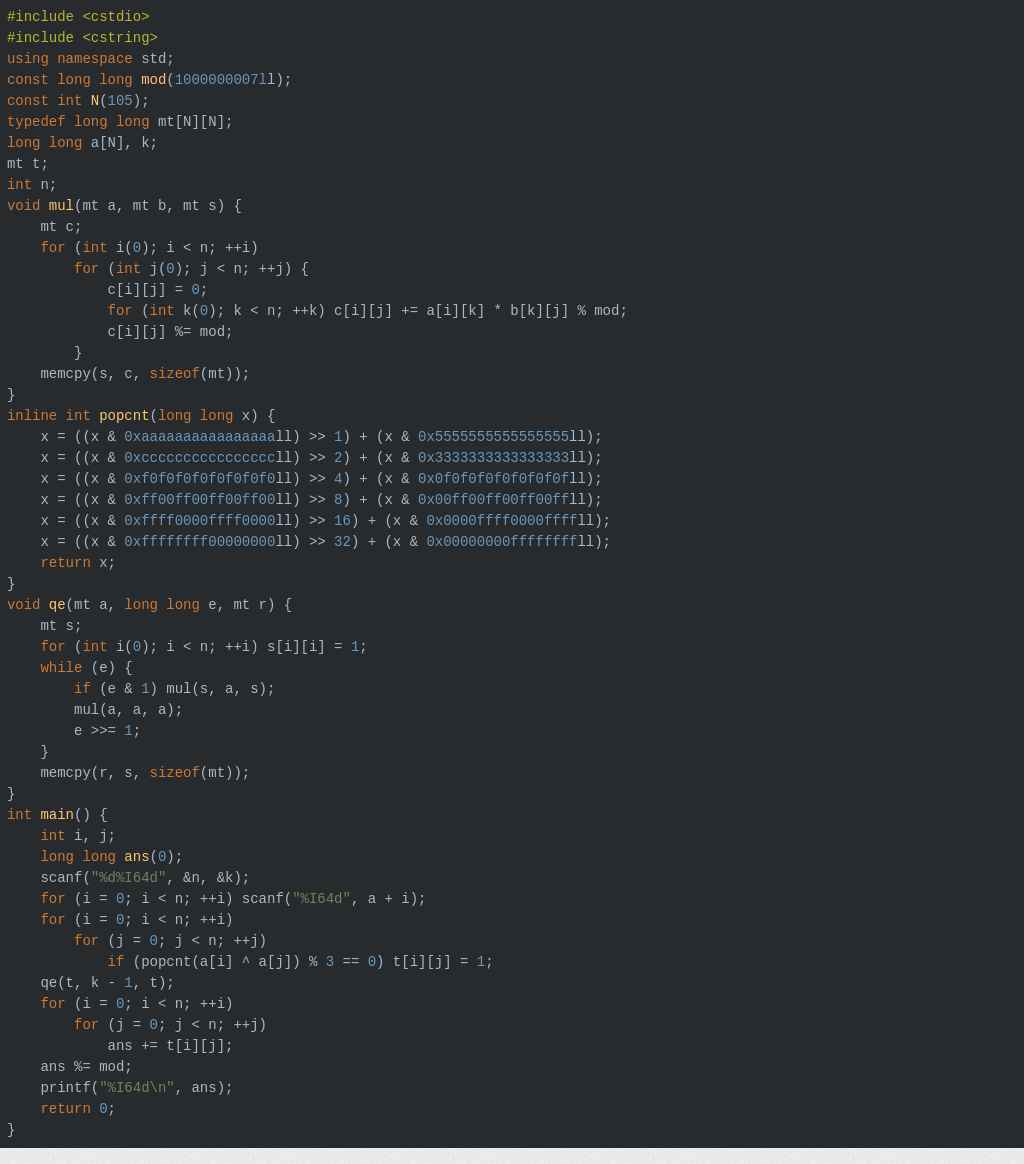
 #include<cstdio>
 #include<cstring>
 #define md 1000000007
 typedef long long LL;
 LL n,k,anss;
 LL a[];
 struct Mat
 {
     LL data[][],x,y;
     Mat()
     {
         memset(data,,sizeof(data));
         x=y=;
     }
     Mat operator*(const Mat& b)
     {
         Mat temp;
         LL i,j,k;
         for(i=;i<=x;i++)
             for(j=;j<=b.y;j++)
                 for(k=;k<=y;k++)
                     temp.data[i][j]=(data[i][k]*b.data[k][j]+temp.data[i][j])%md;
         temp.x=x;
         temp.y=b.y;
         return temp;
     }
     Mat& operator*=(const Mat& b)
     {
         return (*this)=(*this)*b;
     }
     Mat& operator=(const Mat& b)
     {
         memcpy(data,b.data,sizeof(data));
         x=b.x;
         y=b.y;
         return *this;
     }
 }ma,o,bbb,ccc;
 Mat pow(const Mat& a,LL b)
 {
     Mat ans=o;
     if(b==)    return ans;
     Mat base=a;
     while(b!=)
     {
         if(b&!=)    ans*=base;
         base*=base;
         b>>=;
     }
     return ans;
 }
 int main()
 {
     LL i,j;
     scanf("%I64d%I64d",&n,&k);
     for(i=;i<=n;i++)
         scanf("%I64d",&a[i]);
     ma.x=ma.y=n;
     for(i=;i<=n;i++)
         for(j=;j<=n;j++)
             ma.data[i][j]=(__builtin_popcountll(a[i]^a[j])%==);
     o.x=o.y=n;
     for(i=;i<=n;i++)
         for(j=;j<=n;j++)
             o.data[i][j]=(i==j);
     bbb=pow(ma,k-);
     ccc.x=;ccc.y=n;
     for(i=;i<=n;i++)
         ccc.data[][i]=;
     ccc*=bbb;
     for(i=;i<=n;i++)
         anss=(anss+ccc.data[][i])%md;
     printf("%I64d",anss);
     return ;
 }