HDU 4565 So Easy! 数学 + 矩阵 + 整体思路化简

http://acm.hdu.edu.cn/showproblem.php?pid=4565

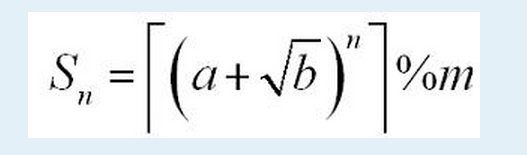
首先知道里面那个东西，是肯定有小数的，就是说小数部分是约不走的，（因为b限定了不是一个完全平方数）。

因为(a - 1)^2 < b < (a ^ 2)，所以其不是完全平方数，假如是，那么设其为c，则有a - 1 < c < a，这是矛盾的

所以，向上取整这个步骤，是必不可少的了。

那么，我在它后面加上一个< 1的数，同时使得它们结合成为整数，那就相当于帮它取整了。根据二项式定理

(a + sqrt(b)) ^ n + (a - sqrt(b)) ^ n，其中的奇数次幂，都抵消了。所以这个是一个整数，而且(a - sqrt(b)) ^ n也是小于1的。刚好符合我们的要求。

所以Sn = (a + sqrt(b)) ^ n + (a - sqrt(b)) ^ n

现在就是要找Sn和S（n +１）的关系那些。

化简的时候，整体化简，

设

x = a + sqrt(b)

y = a - sqrt(b)

x + y = 2 * a

x * y = a * a - b

那么Sn = x^n + y^n  = (x + y) * (x^(n - 1) + y^(n - 1)) - (x * y) * (x ^ (n - 2) + y ^ (n - 2))

就是Sn = (x + y) * S(n - 1) - (x * y) * (S(n - 2))

然后矩阵快速幂

过程中要不断取模，防止中途溢出。

跪了。这题真的跪了。

#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <assert.h>
#define IOS ios::sync_with_stdio(false)
using namespace std;
#define inf (0x3f3f3f3f)
typedef long long int LL;

#include <iostream>
#include <sstream>
#include <vector>
#include <set>
#include <map>
#include <queue>
#include <string>
#include <bitset>
LL a, b, n, m;
const int maxn = ;
struct Matrix {
    LL a[maxn][maxn];
    int row;
    int col;
};
struct Matrix matrix_mul  (struct Matrix a, struct Matrix b, int MOD) {  //求解矩阵a*b%MOD
    struct Matrix c = {};  //这个要多次用到，栈分配问题，maxn不能开太大，
    //LL的时候更加是，空间是maxn*maxn的，这样时间用得很多，4和5相差300ms
    c.row = a.row; //行等于第一个矩阵的行
    c.col = b.col; //列等于第二个矩阵的列
    for (int i = ; i <= a.row; i++) { //枚举第一个矩阵的行
        for (int j = ; j <= b.col; j++) { //枚举第二个矩阵的列，其实和上面数值一样
            for (int k = ; k <= b.row; k++) { //b中的一列中，有“行”个元素 notice
                c.a[i][j] += a.a[i][k] * b.a[k][j];
                c.a[i][j] %= MOD;
            }
            c.a[i][j] = (c.a[i][j] + MOD) % MOD; //如果怕出现了负数取模的话。可以这样做
        }
    }
    return c;
}
struct Matrix quick_matrix_pow(struct Matrix ans, struct Matrix base, int n, int MOD) {
//求解a*b^n%MOD
    while (n) {
        if (n & ) {
            ans = matrix_mul(ans, base, MOD);//传数组不能乱传,不满足交换律
        }
        n >>= ;
        base = matrix_mul(base, base, MOD);
    }
    return ans;
}

void work() {
    if (n == ) {
        cout <<  * a % m << endl;
        return;
    }
    if (n == ) {
        cout << ( * a * a +  * b) % m << endl;
        return;
    }
    Matrix ma_a = {};
    ma_a.row = , ma_a.col = ;
    ma_a.a[][] =  * a * a +  * b, ma_a.a[][] =  * a;

    Matrix ma_b = {};
    ma_b.row = , ma_b.col = ;
    ma_b.a[][] =  * a, ma_b.a[][] = ;
    ma_b.a[][] = -(a * a - b), ma_b.a[][] = ;

    Matrix ans = quick_matrix_pow(ma_a, ma_b, n - , m);
    cout << ans.a[][] << endl;
}
int main() {
#ifdef local
    freopen("data.txt", "r", stdin);
//    freopen("data.txt", "w", stdout);
#endif
    IOS;
    while (cin >> a >> b >> n >> m) work();
    return ;
}