微信小程序---账号注册与开发工具
(1)申请帐号
进入小程序注册页 根据指引填写信息和提交相应的资料,就可以拥有自己的小程序帐号。
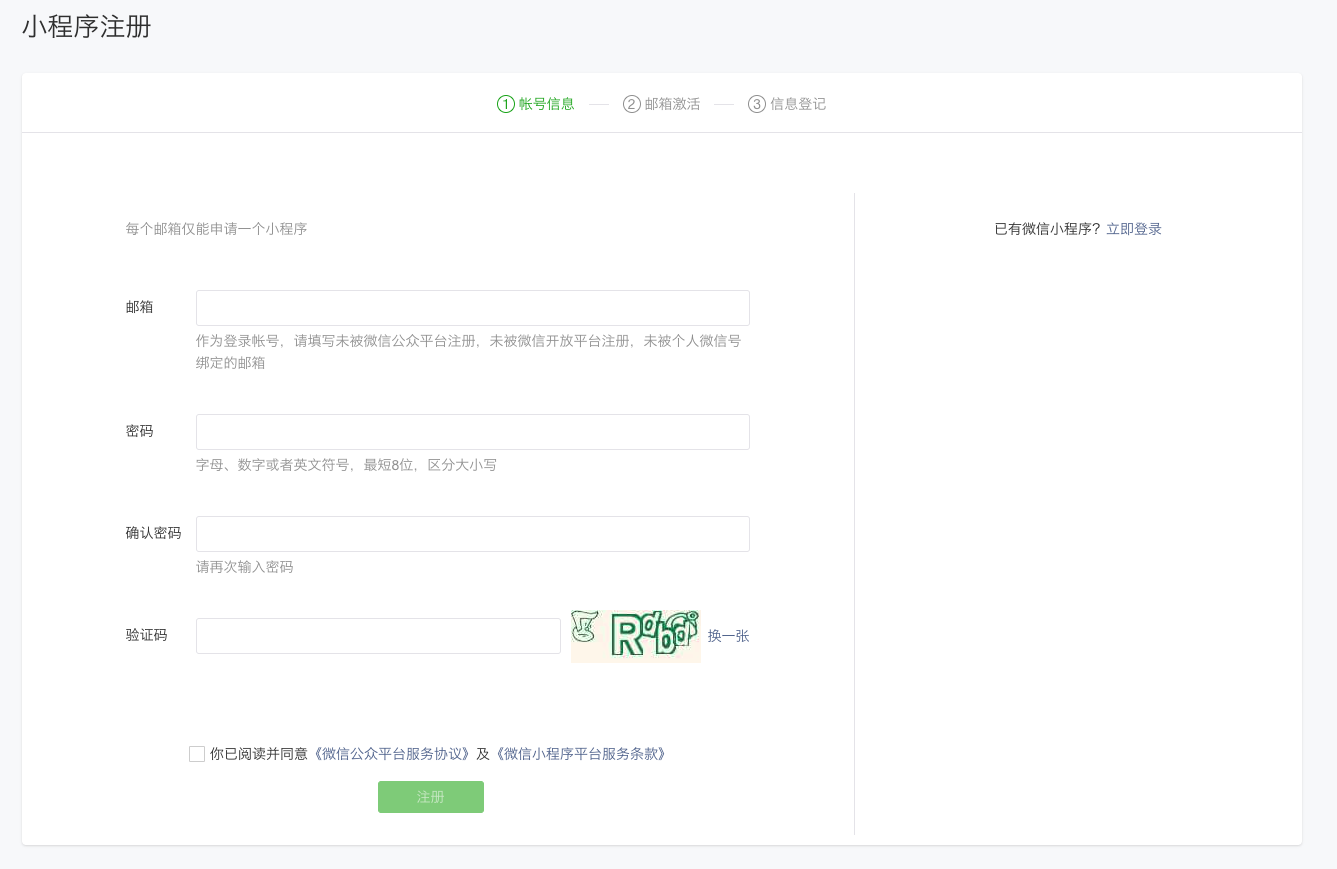
在这个小程序管理平台,你可以管理你的小程序的权限,查看数据报表,发布小程序等操作。
登录 小程序后台 ,我们可以在菜单 “设置” 就可以看到小程序的 AppID 了 。小程序的 AppID 相当于小程序平台的一个身份证,后续你会在很多地方要用到 AppID (注意这里要区别于服务号或订阅号的 AppID)。有了小程序帐号之后,接下俩需要一个工具来开发小程序。
(2)安装开发工具
前往 开发者工具下载页面 ,根据自己的操作系统下载对应的安装包进行安装,有关开发者工具更详细的介绍可以查看 《开发者工具介绍》 。
打开小程序开发者工具,用微信扫码登录开发者工具,准备开发小程序!
.
微信小程序---账号注册与开发工具的更多相关文章
- 微信小程序账号注册
想要开发微信小程序,先注册账号申请APPID. 第一步:百度搜索"微信公众平台" 第二步:立即注册 进入注册页面 区别: 订阅号: 订阅号在文件夹里,订阅号消息 一天只能推送一次, ...
- webstorm开发微信小程序代码提醒(webstorm开发工具)
使用了微信提供的开发工具是真心难用,卡顿厉害.中英文切写注释换相当不爽.还没办法多开窗口,相信大家也遇到过这种现象. 下边我们介绍下webstorm来开发微信小程序的一些配置: File---sett ...
- 微信小程序购物商城系统开发系列-工具篇
微信小程序开放公测以来,一夜之间在各种技术社区中就火起来啦.对于它 估计大家都不陌生了,对于它未来的价值就不再赘述,简单一句话:可以把小程序简单理解为一个新的操作系统.新的生态,未来大部分应用场景都将 ...
- 微信小程序购物商城系统开发系列
微信小程序购物商城系统开发系列 微信小程序开放公测以来,一夜之间在各种技术社区中就火起来啦.对于它 估计大家都不陌生了,对于它未来的价值就不再赘述,简单一句话:可以把小程序简单理解为一个新的操作系统. ...
- 微信小程序--家庭记账本开发--01
微信小程序的开发准备与开发工具的学习 在这次寒假伊始,临近春节,学习进程有所拉下,现在补上.寻找了好多网站的相关学习视频,包括微信公众平台关于小程序这方面也有好多相关资料供查阅. 1.开发准备: 首先 ...
- 微信小程序开发系列一:微信小程序的申请和开发环境的搭建
我最近也刚刚开始微信小程序的开发,想把我自学的一些心得写出来分享给大家. 这是第一篇,从零开始学习微信小程序开发.主要是小程序的注册和开发环境的搭建. 首先我们要在下列网址申请一个属于自己的微信小程序 ...
- 微信小程序购物商城系统开发系列-目录结构
上一篇我们简单介绍了一下微信小程序的IDE(微信小程序购物商城系统开发系列-工具篇),相信大家都已经蠢蠢欲试建立一个自己的小程序,去完成一个独立的商城网站. 先别着急我们一步步来,先尝试下写一个自己的 ...
- [RN] React Native代码转换成微信小程序代码的转换引擎工具
React Native代码转换成微信小程序代码的转换引擎工具 https://github.com/areslabs/alita
- 从微信小程序到鸿蒙js开发【11】——页面路由
目录: 1.router.push()&wx.navigateTo() 2.router.replace()&wx.redirectTo() 3.router.back()&w ...
随机推荐
- 1.import和include区别 2.NSLog 和printf区别 3.创建对象做的事情 4. 类和对象方法比较 5 匿名对象优缺点 6. 封装 7.作用域范围 8.id和instancetype 9.自定义构造方法规范 10.nil和Nil及NULL、NSNull区别
1.import和include的区别: import可以防止头文件的重复包含 2.NSLog 和printf的区别: 1,NSLog可以自动换行, 输出调试信息, printf不能. 2,NSLog ...
- 创建oracle数据库job服务
创建oracle数据库job服务:PlSqlDev操作job https://www.baidu.com/link?url=5vXhw0IqjvWEAgGSIYsSEVPvJb6njGkJ-_P_VF ...
- [Codeforces 507E] Breaking Good
[题目链接] https://codeforces.com/contest/507/problem/E [算法] 首先BFS求出1到其余点的最短路 , N到其余点的最短路,记为distA[]和dist ...
- 【HNOI 2008】 越狱
[题目链接] 点击打开链接 [算法] 显然,越狱情况数 = 总情况数 - 不能越狱的情况数 很容易发现,总情况数 = M^N 不能越狱的情况数怎么求呢? 我们发现,不能越狱的情况,其实就是第一个人任选 ...
- less 语法
1 变量 less的变量使用@开头 1.1 demo @colorRed:red; @colorBlue:blue; .demo{ color:@colorRed; background-color: ...
- 01_传智播客iOS视频教程_课程介绍与知识点回顾
OC语法中static关键字不能修饰属性,也不能修饰方法,只能修饰方法中的局部变量.static修饰局部变量之后把局部变量变成静态变量.当方法执行完之后这个变量不会被回收.下次再执行这个方法的时候这个 ...
- bzoj 3830: [Poi2014]Freight【dp】
参考:https://blog.csdn.net/zqh_wz/article/details/52953516 妙啊 看成分段问题,因为火车只能一批一批的走(易证= =)设f[i]为到i为止的车都走 ...
- [USACO 2012 Open Gold] Bookshelf【优化dp】
传送门1:http://www.usaco.org/index.php?page=viewproblem2&cpid=138 传送门2:http://www.lydsy.com/JudgeOn ...
- 51nod 1874 字符串排序
1874 字符串排序 基准时间限制:1 秒 空间限制:131072 KB 分值: 5 难度:1级算法题 收藏 关注 定义一个字符串的无序度为所有位置后面的字母比该位置的字母小的总数之和.比如&q ...
- AngularJs 的ng-include指令的使用
AngularJs通过指令ng-include来将页面中共用的模块分离出来,这个功能和mvc里面的分部页的作用一样的. 先看文件的结构: 父页面: <!DOCTYPE html> < ...
