数据结构 - 链栈的实行（C语言）

一、什么是链栈？

链栈：是指利用链式存储结构实现的栈。

想想看栈只是栈顶来做插入和删除操作，栈顶放在链栈的头部还是尾部呢？由于单链表有头指针，而栈顶指针也是必须的，那干吗不让它俩合二为一呢，所以比较好的办法是把栈顶放在链栈的头部（如下图所示)。另外，都已经有了栈顶在头部了，单链表中比较常用的头结点也就失去了意义，通常对于链栈来说，是不需要头结点的。

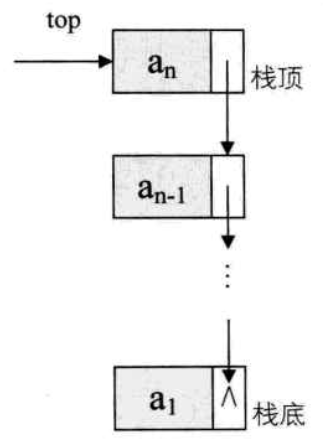
对于空栈来说，链表原定义是头指针指向空，那么链栈的空其实就是 top=NULL 的时候。

链栈的结构代码如下:

typedef int ElemType; /* ElemType类型根据实际情况而定，这里假设为int */

/* 链栈结点结构 */
typedef struct StackNode
{
	ElemType data;
	struct StackNode *next;
}StackNode;

/* 链栈结构 */
typedef struct
{
	StackNode  *top;
	int count;
}LinkStack;

链栈的操作绝大部分都和单链表类似，只是在插入和删除上，特殊一些。

顺序栈与链栈的区别

两者在时间复杂度上是一样的，均为 O(1)。对于空间性能，顺序栈需要事先确定一个固定的长度，可能会存在内存空间浪费的问题，但它的优势是存取时定位很方便，而链栈则要求每个元素都有指针域，这同时也增加了一些内存开销，但对于栈的长度无限制。所以它们的区别和线性表中讨论的一样，如果栈的使用过程中元素变化不可预料，有时很小，有时非常大，那么最好是用链栈，反之，如果它的变化在可控范围内，建议使用顺序栈会更好一些。

二、基本操作

2.1 初始化栈操作

实现代码如下：

// 初始化栈操作
Status initStack(LinkStack **stack)
{
	// 注意要给链栈分配内存
	*stack = (LinkStack *)malloc(sizeof(LinkStack));

	(*stack)->top = NULL; // 链栈的空其实就是 top=NULL 的时候
	(*stack)->count = 0;

	return TRUE;
}

2.2 进栈操作

对于链栈的进栈 push 操作，假设元素值为 e 的新结点是 s，top 为栈顶指针，示意图如下图所示：

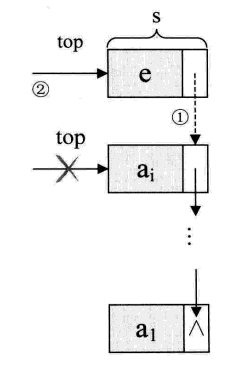
实现代码如下：

// 进栈操作
Status push(LinkStack *stack, ElemType e)
{
	StackNode  *s = (StackNode  *)malloc(sizeof(StackNode));
	s->data = e;
	s->next = stack->top; // 把当前的栈顶元素赋值给新结点的直接后继，见图中①
	stack->top = s; // 将新的结点s赋值给栈顶指针，见图中②
	stack->count++;

	return TRUE;
}

2.3 出栈操作

至于链栈的出栈 pop 操作，也是很简单的三句操作。假设变量 p 用来存储要删除的栈顶结点，将栈顶指针下移一位，最后释放 p 即可，如下图所示：

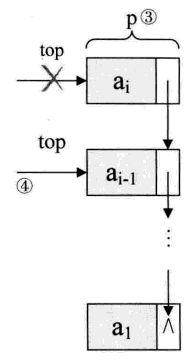
// 出栈操作
Status pop(LinkStack *stack, ElemType *e)
{
	StackNode  *p;
	if (isEmpty(stack))
		return FALSE;
	*e = stack->top->data;
	p = stack->top; // p用来存储要删除的栈顶结点，见图中③
	stack->top = stack->top->next; // 使得栈顶指针下移一位，指向后一结点，见图中④
	free(p); // 释放结点p
	stack->count--;

	return TRUE;
}

链栈的进栈 push 和出栈 pop 操作都很简单，没有任何循环操作，时间复杂度均为 O(1)。

2.4 遍历栈操作

实现代码如下：

// 遍历栈操作
Status traverseStack(LinkStack *stack)
{
	StackNode  *p;
	p = stack->top;
	while (p)
	{
		printf("%d ", p->data);
		p = p->next;
	}
	printf("\n");

	return TRUE;
}

三、完整程序

#include <stdio.h>
#include <stdlib.h> 

#define TRUE 1
#define FALSE 0
#define MAXSIZE 20 /* 存储空间初始分配量 */

typedef int Status;
typedef int ElemType; /* ElemType类型根据实际情况而定，这里假设为int */

/* 链栈结点结构 */
typedef struct StackNode
{
	ElemType data;
	struct StackNode *next;
}StackNode;

/* 链栈结构 */
typedef struct
{
	StackNode  *top;
	int count;
}LinkStack;

Status initStack(LinkStack **stack); // 初始化栈操作
Status push(LinkStack *stack, const ElemType e); // 进栈操作
Status pop(LinkStack *stack, ElemType *e); // 出栈操作
Status traverseStack(LinkStack *stack); // 遍历栈操作
Status clearStack(LinkStack *stack); // 清空栈操作
Status isEmpty(LinkStack *stack); // 判断是否为空
Status getTop(LinkStack *stack, ElemType *e); // 获得栈顶元素
int getLength(LinkStack *stack); // 获取栈的长度

// 初始化栈操作
Status initStack(LinkStack **stack)
{
	// 注意要给链栈分配内存
	*stack = (LinkStack *)malloc(sizeof(LinkStack));

	(*stack)->top = NULL; // 链栈的空其实就是 top=NULL 的时候
	(*stack)->count = 0;

	return TRUE;
}

// 进栈操作
Status push(LinkStack *stack, ElemType e)
{
	StackNode  *s = (StackNode  *)malloc(sizeof(StackNode));
	s->data = e;
	s->next = stack->top; // 把当前的栈顶元素赋值给新结点的直接后继，见图中①
	stack->top = s; // 将新的结点s赋值给栈顶指针，见图中②
	stack->count++;

	return TRUE;
}

// 出栈操作
Status pop(LinkStack *stack, ElemType *e)
{
	StackNode  *p;
	if (isEmpty(stack))
		return FALSE;
	*e = stack->top->data;
	p = stack->top; // p用来存储要删除的栈顶结点，见图中③
	stack->top = stack->top->next; // 使得栈顶指针下移一位，指向后一结点，见图中④
	free(p); // 释放结点p
	stack->count--;

	return TRUE;
}

// 遍历栈操作
Status traverseStack(LinkStack *stack)
{
	StackNode  *p;
	p = stack->top;
	while (p)
	{
		printf("%d ", p->data);
		p = p->next;
	}
	printf("\n");

	return TRUE;
}

// 清除栈操作
Status clearStack(LinkStack *stack)
{
	StackNode  *p;
	StackNode  *q;
	p = stack->top;
	while (p)
	{
		q = p;
		p = p->next;
		free(q);
	}
	stack->count = 0;

	return TRUE;
}

// 判断是否为空栈
Status isEmpty(LinkStack *stack)
{
	return stack->count == 0 ? TRUE : FALSE;
}

// 获得栈顶元素
Status getTop(LinkStack *stack, ElemType *e)
{
	if (stack->top == NULL)
		return FALSE;
	else
		*e = stack->top->data;

	return TRUE;
}

// 获得栈的长度
int getLength(LinkStack *stack)
{
	return stack->count;
}

int main()
{
	// 初始化栈
	LinkStack *stack;
	if (initStack(&stack) == TRUE)
		printf("初始化链栈成功！\n\n");

	// 入栈操作
	for (int j = 1; j <= 10; j++)
		push(stack, j);
	printf("入栈操作（0-10）!\n\n");

	// 出栈操作
	int e;
	pop(stack, &e);
	printf("弹出的栈顶元素e=%d\n\n", e);

	// 遍历栈
	printf("遍历栈，栈中元素依次为：");
	traverseStack(stack);
	printf("\n");

	// 获得栈顶元素
	getTop(stack, &e);
	printf("栈顶元素 e=%d 栈的长度为%d\n\n", e, getLength(stack));

	// 判断是否为空栈
	printf("栈空否：%d(1:空 0:否)\n\n", isEmpty(stack));

	// 清空栈
	clearStack(stack);
	printf("清空栈后，栈空否：%d(1:空 0:否)\n\n", isEmpty(stack));

	return 0;
}

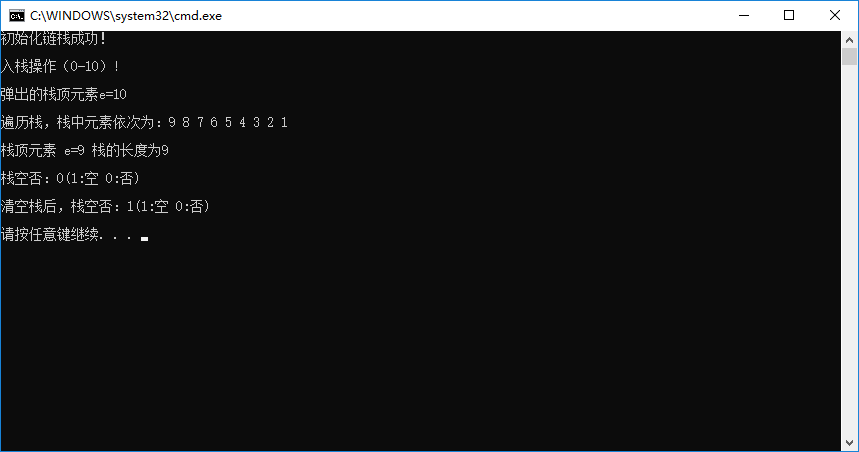
输出结果如下图所示：

参考：

《大话数据结构 - 第4章》 栈与队列