数据结构——平衡二叉树（AVLTree）

　3.平衡二叉树

　　平衡二叉树，又称AVL树，它是一种特殊的二叉排序树。

　　3.1 平衡二叉树的四种自旋

　　这个左旋、右旋，在方向上和我观念里的是相反的。

查了之后才知道：

1、外侧插入：LL、RR，都是在最边边上。
2、内侧插入：LR、RL，往里面来了些。

　　（1）LL旋转和RR旋转：

   

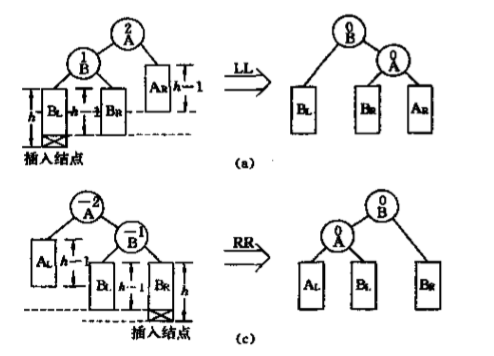
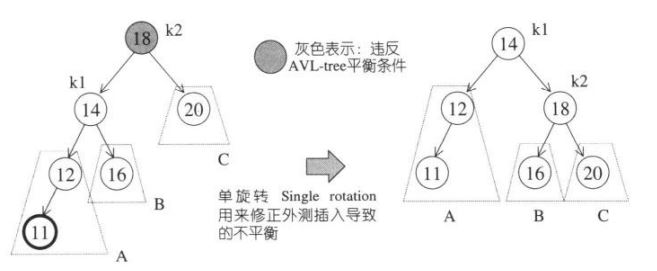
void RR_Rotate(AVLTree *root){
    AVLTreeNode* rchild = (*root)->Right;
    (*root)->Right = rchild->Left;
    rchild->Left = *root;
    *root = rchild;
}

void LL_Rotate(AVLTree *root) {
    AVLTreeNode* lchild = (*root)->Left;
    (*root)->Left = lchild->Right;
    lchild->Right = *root;
    *root = lchild;
}

　　（2）LR，RL型旋转（插入的节点在CL上 还是CR上是没有影响的）

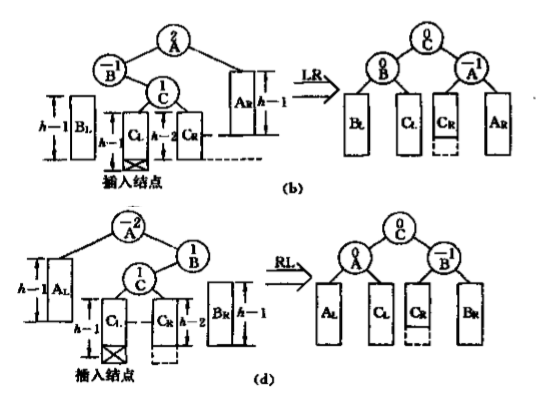
　　LR型旋转图解

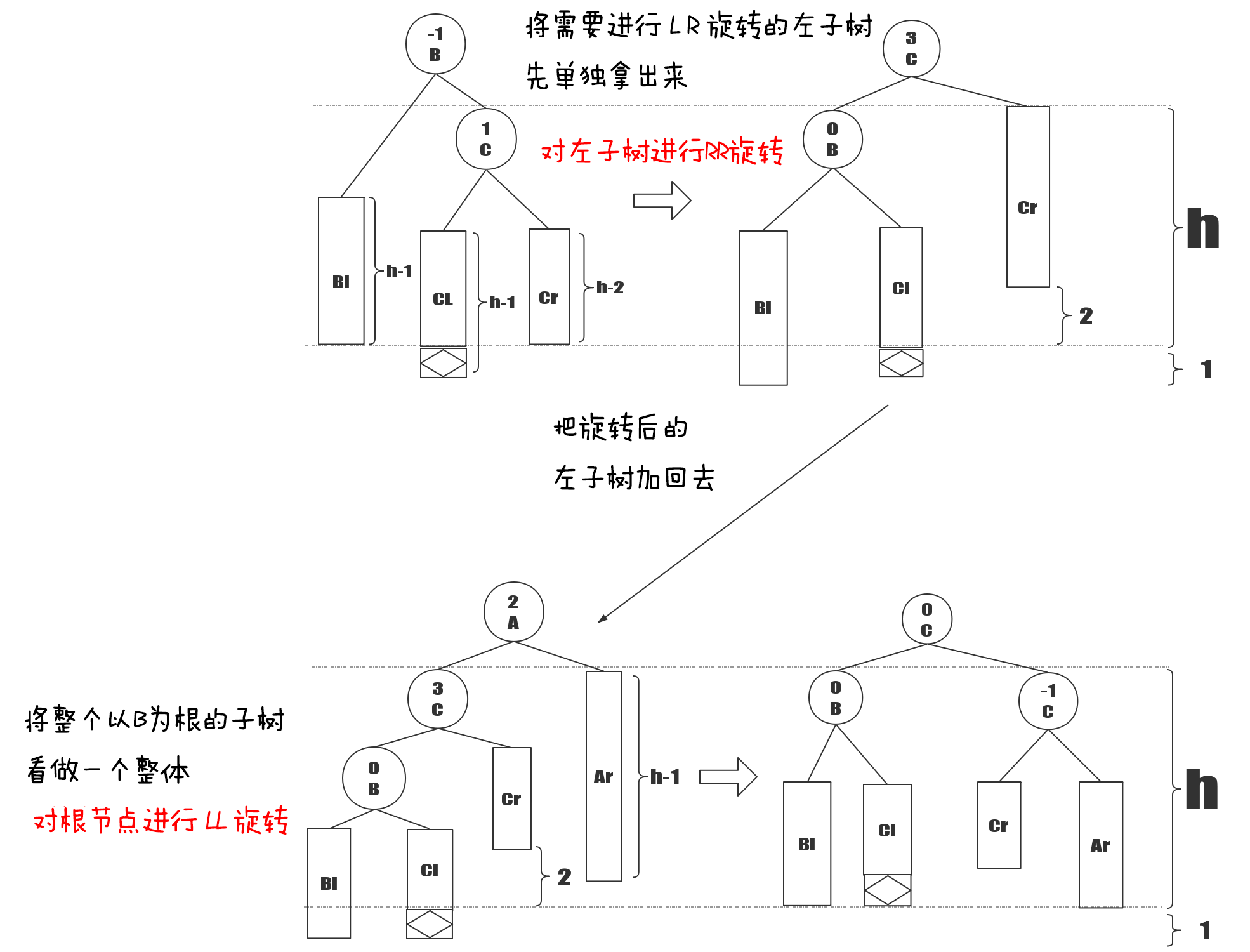
void LR_Rotate(AVLTree *root) {
    RR_Rotate(&(*root)->Left);
    return LL_Rotate(root);
}
void RL_Rotate(AVLTree *root) {
    LL_Rotate(&(*root)->Right);
    RR_Rotate(root);
}

小结：几个子树在水平位置上顺序是不会变的！根节点和根节点的子树在水平上的逻辑位置也是不会变的。

---

　　3.2 平衡二叉树的插入

　　插入算法就是出现不平衡状态时，判断需要使用哪种旋转方式来使得二叉树保持平衡：

AVLTree InsertAVLTree(AVLTree root, int x) {
    if (root == NULL) {
        root = new AVLTreeNode;
        root->Left = NULL;
        root->Right = NULL;
        root->data = x;
        return root;
    }
    if (x > root->data) {
            root->Right = InsertAVLTree(root->Right, x);
            //递归返回插入位置的父节点或者祖父……，如果失去了平衡
            ) {
                //如果插入的值大于,当前节点的左孩子节点，说明该节点是插在root的右子树上的
                if (x > root->Left->data) RR_Rotate(&root);
                else RL_Rotate(&root);
            }
    }

    else if (x < root->data) {
        root->Left = InsertAVLTree(root->Left, x);
        ) {
            if (x < root->Left->data) LL_Rotate(&root);
            else LR_Rotate(&root);
        }
    }
    else {
        cout << "the number is already included." << endl;
        return NULL;
    }
    return root;
}

---

　3.3 平衡二叉树的删除

　　 之前写过二叉排序树的节点的删除的话，这里会好写很多，就是多出来一个判断从哪个子树删除节点的问题。

void AVLTreeDel(AVLTree *root, int data)
{
    if (!*root) {
        cout << "delete failed" << endl;
        return;
    }
    AVLTreeNode *p = *root;
    if (data == p->data) {
        //左右子树都非空
        if (p->Left && p->Right) {
            //在高度更大的那个子树上进行删除操作
            //进左子树，右转到底，进右子树，左转到底，转弯碰壁，杀孩子。
            if (height(p->Left) > height(p->Right)) {
                AVLTreeNode *pre=NULL,*q = p->Left;
                if (!q->Right)
                    q->Right = p->Right;
                else {
                    while (q->Right) {
                        pre = q;
                        q = q->Right;
                    }
                    pre->Right = q->Left;
                    q->Left = p->Left;
                    q->Right = p->Right;
                }
                *root = q;
            }
            else {
                AVLTreeNode *pre = NULL, *q = p->Right;
                if (!q->Left)
                    q->Left = p->Left;
                else {
                    while (q->Left) {
                        pre = q;
                        q = q->Left;
                    }
                    pre->Left = q->Right;
                    q->Left = p->Left;
                    q->Right = p->Right;
                }
                *root=q;
            }
        }
        else
            (*root) = (*root)->Left ? (*root)->Left : (*root)->Right;
        delete p;
    }
    else if (data < p->data){//要删除的节点在左子树中
        //在左子树中进行递归删除
        AVLTreeDel(&(*root)->Left, data);
        //判断是否仍然满足平衡条件
        ){
            //如果当前节点右孩子的左子树更高
            if (height(p->Right->Left) > height(p->Right->Right))
                RL_Rotate(root);
            else
                RR_Rotate(root);
        }
    }
    else{
        AVLTreeDel(&(*root)->Right, data);
        ) {
            if (height((*root)->Left->Left) > height((*root)->Left->Right))
                LL_Rotate(root);
            else
                LR_Rotate(root);
        }
    }
}

https://www.2cto.com/kf/201702/556250.html

完整代码（2019.1.20）：

#pragma once
#include "top.h"

typedef BTreeNode AVLTreeNode, *AVLTree;

void RR_Rotate(AVLTree *root){
    AVLTreeNode* Right = (*root)->Right;
    (*root)->Right = Right->Left;
    Right->Left = *root;
    *root = Right;
}

void LL_Rotate(AVLTree *root) {
    AVLTreeNode* Left = (*root)->Left;
    (*root)->Left = Left->Right;
    Left->Right = *root;
    *root = Left;
}
void LR_Rotate(AVLTree *root) {
    RR_Rotate(&(*root)->Left);
    return LL_Rotate(root);
}
void RL_Rotate(AVLTree *root) {
    LL_Rotate(&(*root)->Right);
    RR_Rotate(root);
}
AVLTree AVLTreeInsert(AVLTree root, int x) {
    if (root == NULL) {
        root = new AVLTreeNode;
        root->Left = NULL;
        root->Right = NULL;
        root->data = x;
        return root;
    }
    if (x > root->data) {
            root->Right = AVLTreeInsert(root->Right, x);
            //递归返回插入位置的父节点或者祖父……，如果失去了平衡
            ) {
            //如果插入的值大于,当前节点的右孩子节点，说明该节点是插在root的右子树上的
                //if (x > root->Left->data) RR_Rotate(&root);不能保证该节点一定有左子树
                if (x > root->Right->data)RR_Rotate(&root);
                else RL_Rotate(&root);
            }
    }
    else if (x < root->data) {
        root->Left = AVLTreeInsert(root->Left, x);
        ) {
            if (x < root->Left->data) LL_Rotate(&root);
            else LR_Rotate(&root);
        }
    }
    else {
        cout << "the number is already included." << endl;
        return NULL;
    }
    return root;
}

AVLTree AVLTreeCreat(int *a, int length) {
    AVLTree T = NULL;
    ; i < length; i++) {
        T = AVLTreeInsert(T, a[i]);
    }
    return T;
}
AVLTreeNode* AVLFind(AVLTree T, int x) {
    AVLTreeNode *p = T;
    while (p) {
        if (x == p->data) break;
        p = x > p->data ? p->Right : p->Left;
    }
    return p;
}

AVLTree AVLMax(AVLTree p)
{
    if (!p) return NULL;
    if (p->Right == NULL)
        return p;
    return AVLMax(p->Right);
}

AVLTree AVLMin(AVLTree p)
{
    if (!p)
        return NULL;
    if (p->Left == NULL)
        return p;
    return AVLMin(p->Left);
}

void AVLTreeDel(AVLTree *root, int data)
{
    if (!*root) {
        cout << "delete failed" << endl;
        return;
    }
    AVLTreeNode *p = *root;
    if (data == p->data) {
        //左右子树都非空
        if (p->Left && p->Right) {
            //在高度更大的那个子树上进行删除操作
            //进左子树，右转到底，进右子树，左转到底，转弯碰壁，杀孩子。
            if (height(p->Left) > height(p->Right)) {
                AVLTreeNode *pre=NULL,*q = p->Left;
                if (!q->Right)
                    q->Right = p->Right;
                else {
                    while (q->Right) {
                        pre = q;
                        q = q->Right;
                    }
                    pre->Right = q->Left;
                    q->Left = p->Left;
                    q->Right = p->Right;
                }
                *root = q;
            }
            else {
                AVLTreeNode *pre = NULL, *q = p->Right;
                if (!q->Left)
                    q->Left = p->Left;
                else {
                    while (q->Left) {
                        pre = q;
                        q = q->Left;
                    }
                    pre->Left = q->Right;
                    q->Left = p->Left;
                    q->Right = p->Right;
                }
                *root=q;
            }
        }
        else
            (*root) = (*root)->Left ? (*root)->Left : (*root)->Right;
        delete p;
    }
    else if (data < p->data){//要删除的节点在左子树中
        //在左子树中进行递归删除
        AVLTreeDel(&(*root)->Left, data);
        //判断是否仍然满足平衡条件
        ){
            //如果当前节点右孩子的左子树更高
            if (height(p->Right->Left) > height(p->Right->Right))
                RL_Rotate(root);
            else
                RR_Rotate(root);
        }
    }
    else{
        AVLTreeDel(&(*root)->Right, data);
        ) {
            if (height((*root)->Left->Left) > height((*root)->Left->Right))
                LL_Rotate(root);
            else
                LR_Rotate(root);
        }
    }
}

void checkCreat() {
    ;
    );

    ; i < length; i++) {
        cout << a[i] << ",";
    }

    cout << endl;
    AVLTree T = AVLTreeCreat(a, length);
    int t = rand() % length;
    AVLTreeDel(&T, a[t]);
    ; i++) {
        a[i] = a[i + ];
    }

    Preorder(T);
    cout << endl;
    Inorder(T);
    cout << endl;
    Postorder(T);
    cout << endl;
    free(a);
}