Sum Problem

2018-04-22 19:59:52

Sum系列的问题是Leetcode上的一个很经典的系列题，这里做一个简单的总结。

• 167. Two Sum II - Input array is sorted

问题描述：

问题求解：

对于已排序的问题，可以使用双指针在O(n)的时间复杂度内完成求解。

    // 已排序数组，返回indices
    public int[] twoSum(int[] numbers, int target) {
        int i = 0;
        int j = numbers.length - 1;
        while (i < j) {
            if (target > numbers[i] + numbers[j]) i++;
            else if (target < numbers[i] + numbers[j]) j--;
            else break;
        }
        return new int[]{i + 1, j + 1};
    }

• 1. Two Sum

问题描述：

问题求解：

可以使用数据结构中的hash来很高效的解决，具体来说，我们可以建立一个hashmap，用来保存数值和其index，遍历数组，如果说hashmap中存在target - nums[i]，由于题目中明确了只有唯一的解，因此就可以直接确定结果，将这两个数的index返回即可。

    public int[] twoSum3(int[] numbers, int target) {
        int[] result = new int[2];
        HashMap<Integer, Integer> map = new HashMap<>();
        for (int i = 0; i < numbers.length; i++) {
            if (map.containsKey(target - numbers[i])) {
                result[1] = i + 1;
                result[0] = map.get(target - numbers[i]);
                break;
            }
            map.put(numbers[i], i + 1);
        }
        return result;
    }

• 653. Two Sum IV - Input is a BST

问题描述：

Given a Binary Search Tree and a target number, return true if there exist two elements in the BST such that their sum is equal to the given target.

问题求解：

方法一、很容易想到的是二叉搜索树的中序遍历是一个有序数列，如果我们采用中序遍历一次并保存下来，那么问题就变成了上述的已排序数组求two sum的问题。

代码时间复杂度为O(n)。

    ArrayList<Integer> ls = new ArrayList<>();
    public boolean findTarget(TreeNode root, int k) {
        inOrder(root);
        boolean res = false;
        int i = 0;
        int j = ls.size() - 1;
        while (i < j) {
            if (ls.get(i) + ls.get(j) > k) j--;
            else if (ls.get(i) + ls.get(j) < k) i++;
            else {
                res = true;
                break;
            }
        }
        return res;
    }

    void inOrder(TreeNode root) {
        if (root != null) {
            inOrder(root.left);
            ls.add(root.val);
            inOrder(root.right);
        }
    }

方法二、递归遍历，每次递归到某个数就对target - nums[i]进行查找，值得注意的是，在查找过程中要特别注意不能是当前的数，因为同一个数只能出现一次，因此在传参的时候要把当前的结点信息传进去。

代码时间复杂度从理论上来说应该是O(nlogn)。但由于剪枝效应的存在，所以在实际的运行上还是比较高效的。

    public boolean findTarget(TreeNode root, int k) {
        return dfs(root, root, k);
    }

    private boolean dfs(TreeNode root, TreeNode cur, int k) {
        if(cur == null) return false;
        return search(root, cur, k-cur.val) || dfs(root, cur.left, k) || dfs(root, cur.right, k);
    }

    private boolean search(TreeNode root, TreeNode cur, int target) {
        if(root == null) return false;
        if(target == root.val) return root != cur;
        else if (target > root.val) return search(root.right, cur, target);
        else return search(root.left, cur, target);
    }

• 15. 3Sum

问题描述：

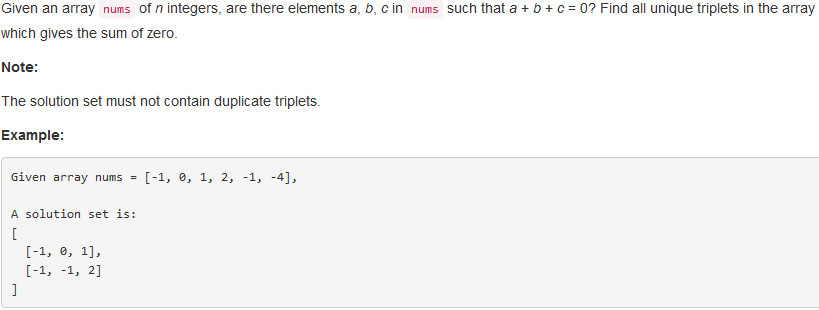
问题求解：

主要的思想就是转化成Two Sum的问题，其中由于结果不能重复，所以我们需要提前对nums进行排序，在排序后，对先后相等的数就可以进行忽略处理了，这样就避免了重复的问题。另外，由于本题中的target = 0，那么在排序后的数组中如果其值大于0，那么也是可以直接排除可能性的，因为其值大于0，其后面的值也必然大于0，因此是不可能存在说三个正数的和为0的。

本题其实也是可以使用dfs + 回溯解决的，但是时间复杂度上会高不少。这里就不多讲解了。

    public List<List<Integer>> threeSum(int[] nums) {
        List<List<Integer>> res = new ArrayList<>();
        Arrays.sort(nums);
        for (int i = 0; i < nums.length - 2; i++) {
            if (i == 0 || (nums[i] <= 0 && nums[i] != nums[i - 1])) {
                int sum = 0 - nums[i];
                int l = i + 1;
                int r = nums.length - 1;
                while (l < r) {
                    if (nums[l] + nums[r] == sum) {
                        res.add(Arrays.asList(nums[i], nums[l], nums[r]));
                        while (l < r && nums[l] == nums[l + 1]) l++;
                        while (l < r && nums[r] == nums[r - 1]) r--;
                        l++;
                        r--;
                    }
                    else if (nums[l] + nums[r] < sum) {
                        while(l < r && nums[l] == nums[l + 1]) l++;
                        l++;
                    }
                    else {
                        while(l < r && nums[r - 1] == nums[r]) r--;
                        r--;
                    }
                }
            }
        }
        return res;
    }

• 16. 3Sum Closest

问题描述：

问题求解：

本质上和Three Sum是一样的。

    public int threeSumClosest(int[] nums, int target) {
        int min = Integer.MAX_VALUE;
        int res = Integer.MAX_VALUE;
        Arrays.sort(nums);
        for (int i = 0; i < nums.length - 2; i++) {
            if (i == 0 || nums[i] != nums[i - 1]) {
                int sum = target - nums[i];
                int l = i + 1;
                int r = nums.length - 1;
                while (l < r) {
                    if (nums[l] + nums[r] == sum) {
                        return target;
                    }
                    else if (nums[l] + nums[r] < sum) {
                        if (min > sum - (nums[l] + nums[r])) {
                            min = sum - (nums[l] + nums[r]);
                            res = nums[i] + nums[l] + nums[r];
                        };
                        while (l < r && nums[l + 1] == nums[l]) l++;
                        l++;
                    }
                    else {
                        if (min > nums[l] + nums[r] - sum) {
                            min = nums[l] + nums[r] - sum;
                            res = nums[i] + nums[l] + nums[r];
                        };
                        while (l < r && nums[r - 1] == nums[r]) r--;
                        r--;
                    }
                }
            }
        }
        return res;
    }

• 18. 4Sum

问题描述：

问题求解：

转化成Three Sum就好了。

    public List<List<Integer>> fourSum(int[] nums, int target) {
        List<List<Integer>> res = new ArrayList<>();
        Arrays.sort(nums);
        for (int i = 0; i < nums.length - 3; i++) {
            if (i == 0 || nums[i] != nums[i - 1]) {
                for (int j = i + 1; j < nums.length - 2; j++) {
                    if (j == i + 1 || nums[j] != nums[j - 1]) {
                        int sum = target - nums[i] - nums[j];
                        int l = j + 1;
                        int r = nums.length - 1;
                        while (l < r) {
                            if (nums[l] + nums[r] == sum) {
                                res.add(Arrays.asList(nums[i], nums[j], nums[l], nums[r]));
                                while (l < r && nums[l + 1] == nums[l]) l++;
                                while (l < r && nums[r - 1] == nums[r]) r--;
                                l++;
                                r--;
                            }
                            else if (nums[l] + nums[r] < sum) {
                                while (l < r && nums[l + 1] == nums[l]) l++;
                                l++;
                            }
                            else {
                                while (l < r && nums[r - 1] == nums[r]) r--;
                                r--;
                            }
                        }
                    }
                }
            }
        }
        return res;
    }

• 416. Partition Equal Subset Sum

问题描述：

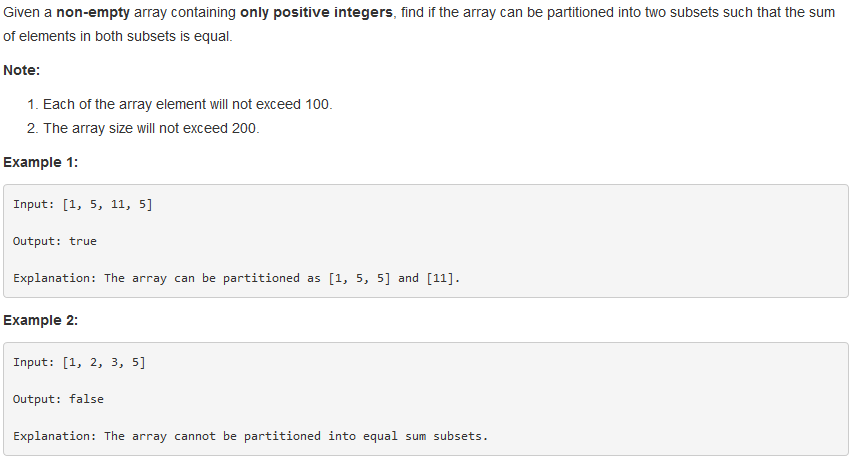
问题求解：

其实就是一个背包问题，这里就是在看能不能挑其中n个物品，使其和为sum/2。当然，首先sum应该是偶数，如果sum奇数，那么就可以直接返回结果。

    public boolean canPartition(int[] nums) {
        int sum = 0;
        for (int i : nums) sum += i;
        if (sum % 2 != 0) return false;
        sum /= 2;
        boolean dp[] = new boolean[sum + 1];
        dp[0] = true;
        for (int num : nums) {
            for (int i = sum; i >= num; i--) {
                dp[i] = dp[i] || dp[i - num];
            }
        }
        return dp[sum];
    }

• 494. Target Sum

问题描述：

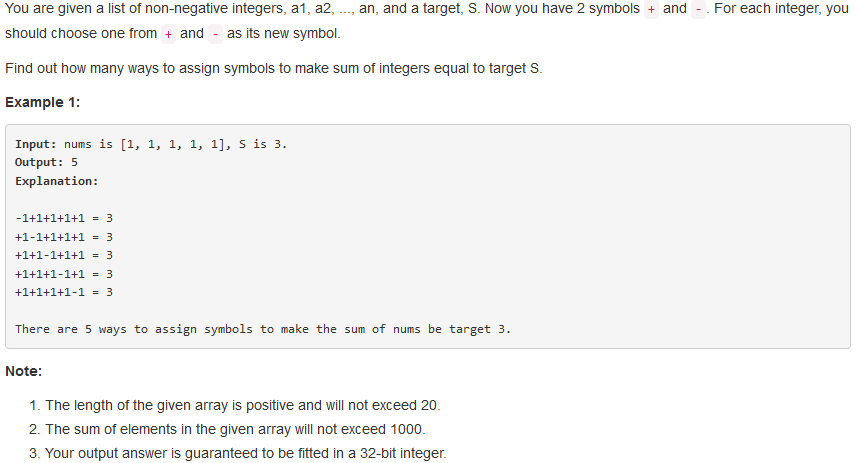
问题求解：

方法一、第一个方法就是暴力搜索，回溯枚举。时间复杂度为指数级。

    public int findTargetSumWays(int[] nums, int S) {
        if (nums.length == 0) return 0;
        return helper(nums, 0, S);
    }

    private int helper(int[] nums, int idx, int S) {
        if (idx == nums.length) {
            if (S == 0) return 1;
            else return 0;
        }
        int res = 0;
        res += helper(nums, idx + 1, S + nums[idx]);
        res += helper(nums, idx + 1, S - nums[idx]);
        return res;
    }

方法二、这个方法很有技巧性，实际上是把原问题转化成了求部分和的问题。不妨设＋部分和为Ｐ，－部分和为Ｑ，则P - Q = S，又P + Q = sum，所以得到2P = S + sum。也就是说求解nums中部分和为(S + sum）/ 2的总个数。由于原问题中指出了数字非负性，所以这种方法是可行的。算法的时间复杂度为伪多项式时间复杂度。

必须要多sum 和 S 的大小进行判断，因为S的大小可能远超sum，这个时候如果不加判断会MLE。

    public int findTargetSumWays(int[] nums, int S) {
        int sum = 0;
        for (int i : nums) sum += i;
        if (sum < S || sum + S < 0 || (sum + S) % 2 != 0) return 0;
        return helper(nums, (sum + S) / 2);
    }

    private int helper(int[] nums, int S) {
        int[] dp = new int[S + 1];
        dp[0] = 1;
        for (int num : nums) {
            for (int i = S; i >= num; i--) {
                dp[i] += dp[i - num];
            }
        }
        return dp[S];
    }