推荐算法——距离算法

迁移到：http://www.bdata-cap.com/newsinfo/1741432.html

本文内容

• 用户评分表
• 曼哈顿（Manhattan）距离
• 欧式（Euclidean）距离
• 余弦相似度（cos simliarity）

推荐算法以及数据挖掘算法，计算“距离”是必须的~最近想搭一个推荐系统，看了一些资料和书《写给程序员的数据挖掘指南》，此书不错，推荐大家看看，讲解得很透彻，有理论有代码，还有相关网站。看完后，你立刻就能把推荐算法应用在你的项目中~

本文先主要说明如何计算物品或用户之间的“距离”，陆续会介绍推荐算法本身~

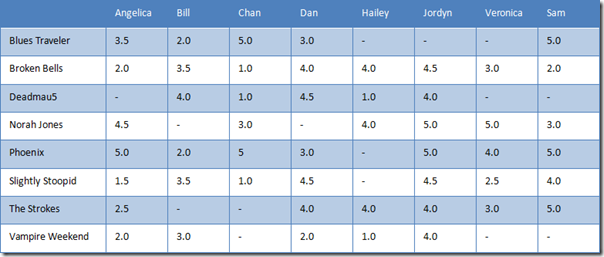
用户评分表

---

大体上，推荐算法可以有两种简单的思路：一是相似的用户，二是相似的物品。

前者，把与你相似的用户喜欢（或购买或评价高）的商品推荐给你，也就是说，如果你跟某个用户的喜好比较接近，那么就可以把这个用户喜欢的，而你不知道（或没浏览过，或没购买过等等）的物品推荐给你。什么叫“喜好接近”，就是对某些物品的评价也好，购买也罢，都比较接近，就认为，你和他喜好相同~

前者的缺陷在于，用户的评价毕竟是少数，想想，你评价过（显式评价）的物品有多少！大多数还是隐式评价，所谓隐式评价，如果你购买一个物品，那显然你会喜欢他，不然也不会买~因此，利用相似的用户是有局限性的。不如利用相似的物品来推荐。

下面“距离”算法主要针对计算用户之间的距离（相似性）。

假设，8个用户对8个乐队进行评分，如下表所示。横向是用户，纵向是乐队。

表 1 用户评分表

曼哈顿（Manhattan）距离

---

计算距离最简单的方法是曼哈顿距离。假设，先考虑二维情况，只有两个乐队 x 和 y，用户A的评价为(x1,y1)，用户B的评价为(x2,y2)，那么，它们之间的曼哈顿距离为

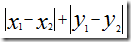
因此，Angelica 与 Bill  之间的曼哈顿距离如下表所示。

表 2 Angelica 与 Bill 的曼哈顿距离

那么，Angelica 与 Bill 之间的曼哈顿距离为 9，即第二列减第三列的绝对值，最后累加。

注意，必须是这两个用户都评分的乐队。

可以推广到n个乐队，即n维向量，用户 A(x1,x2,…,xn)，用户B(y1,y2,…,yn) ，那么它们之间的曼哈顿距离为

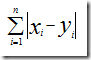
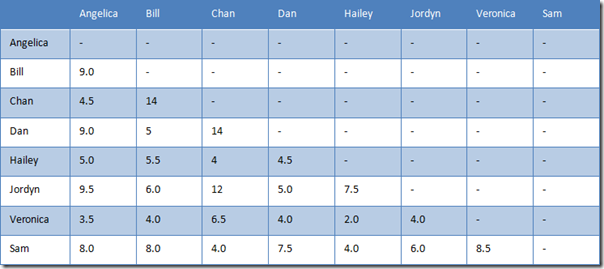
则用户之间的曼哈顿距离如下表所示。

表 3 用户之间的曼哈顿距离

曼哈顿距离的最大好处就是简单，只是加减法而已。如果有几百万个用户，计算起来会很快。

不仅可以扩展到 n 个乐队，当然也可以扩展到 m 个用户，它们可以形成一个矩阵。下面的其他距离同理。

Netflix 当初出 100 万美元奖励给能提升推荐算法 10% 准确率的团队或人，而赢得奖金的人就是使用了一种叫奇异矩阵分解的方法~

欧式（Euclidean）距离

---

除了曼哈顿距离外，还可以计算两个用户之间的欧式距离。

还是先考虑两个乐队 x 和 y 的情况，假设，用户A=(x1,y1)，用户B=(x2,y2)，那么它们之间的欧式距离：

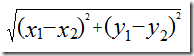
Angelica 与 Bill 之间的曼哈顿距离如下表所示。

表 4 Angelica 与 Bill 的欧式距离

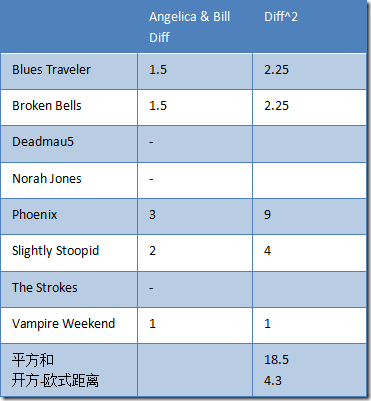
推广到 n 个乐队，用户 A(x1,x2,…,xn)，用户B(y1,y2,…,yn)

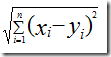
表 5 用户之间的欧式距离

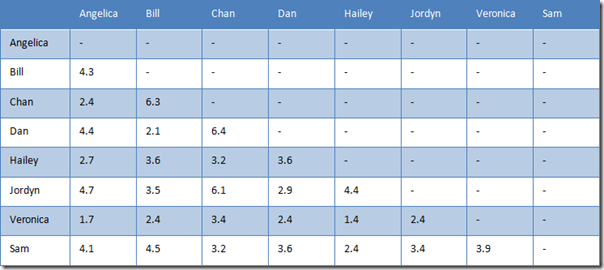
但曼哈顿距离和欧式距离，有个缺点。对比一下 Hailey 与 Veronica 和 Jordyn，Hailey 与前者只有两个乐队评过分，而与后者是五个。换句话说，Hailey 与 Veronica 的距离是基于二维的，而 Hailey 与 Jordyn 是基于五维。想想都觉得有问题。

所以，曼哈顿距离和欧式距离适合数据比较稠密、缺失值比较少的情况。如果缺失值很多，余弦相似度就比较合适。

曼哈顿距离和欧式距离，有通用公式，称为闵可夫斯基距离（Minkowski Distance）。

余弦相似度（cos simliarity）

---

假设，有两个乐队，用户A=(x1,y1)，用户B=(x2,y2)，那么他们之间的余弦相识度为：

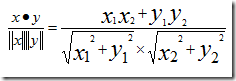
表 6 Angelica 与 Bill 的余弦相似度

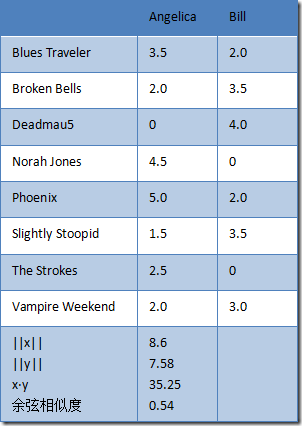
推广到n维，用户A和B，对n个乐队的评分分别为(x1,x2,...,xn)和(y1,y2,...,yn)，则他们之间的余弦相似度为

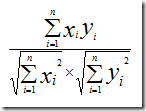
源代码 dis.py

---

#

#  dis.py

#

from math import *

teams = [

    "Blues Traveler", 

    "Broken Bells", 

    "Deadmau5", 

    "Norah Jones", 

    "Phoenix", 

    "Slightly Stoopid", 

    "The Strokes", 

    "Vampire Weekend"

]

users = {

    "Angelica": {

        "Blues Traveler": 3.5,

        "Broken Bells": 2,

        "Norah Jones": 4.5,

        "Phoenix": 5,

        "Slightly Stoopid": 1.5,

        "The Strokes": 2.5,

        "Vampire Weekend": 2

    },

    "Bill": {

        "Blues Traveler": 2,

        "Broken Bells": 3.5,

        "Deadmau5": 4,

        "Phoenix": 2,

        "Slightly Stoopid": 3.5,

        "Vampire Weekend": 3

    },

    "Chan": {

        "Blues Traveler": 5,

        "Broken Bells": 1,

        "Deadmau5": 1,

        "Norah Jones": 3,

        "Phoenix": 5,

        "Slightly Stoopid": 1

    },

    "Dan": {

        "Blues Traveler": 3,

        "Broken Bells": 4,

        "Deadmau5": 4.5,

        "Phoenix": 3,

        "Slightly Stoopid": 4.5,

        "The Strokes": 4,

        "Vampire Weekend": 2

    },

    "Hailey": {

        "Broken Bells": 4,

        "Deadmau5": 1,

        "Norah Jones": 4,

        "The Strokes": 4,

        "Vampire Weekend": 1

    },

    "Jordyn": {

        "Broken Bells": 4.5,

        "Deadmau5": 4,

        "Norah Jones": 5,

        "Phoenix": 5,

        "Slightly Stoopid": 4.5,

        "The Strokes": 4,

        "Vampire Weekend": 4

    },

    "Sam": {

        "Blues Traveler": 5,

        "Broken Bells": 2,

        "Norah Jones": 3,

        "Phoenix": 5,

        "Slightly Stoopid": 4,

        "The Strokes": 5

    },

    "Veronica": {

        "Blues Traveler": 3,

        "Norah Jones": 5,

        "Phoenix": 4,

        "Slightly Stoopid": 2.5,

        "The Strokes": 3

    }

}

def manhattan(rating1, rating2):

    """Computes the Manhattan distance. Both rating1 and rating2 are dictionaries

       of the form {'The Strokes': 3.0, 'Slightly Stoopid': 2.5}"""

    distance = 0

    commonRatings = False 

    for key in rating1:

        if key in rating2:

            distance += abs(rating1[key] - rating2[key])

            commonRatings = True

    if commonRatings:

        return distance

    else:

        return -1 #Indicates no ratings in common

def euclidean(rating1, rating2):

    """Computes the euclidean distance. Both rating1 and rating2 are dictionaries

       of the form {'The Strokes': 3.0, 'Slightly Stoopid': 2.5}"""

    distance = 0

    commonRatings = False 

    for key in rating1:

        if key in rating2:

            distance += pow(rating1[key] - rating2[key],2)

            commonRatings = True

    if commonRatings:

        return sqrt(distance)

    else:

        return -1 #Indicates no ratings in common

def minkowski(rating1, rating2, r):

    """Computes the minkowski distance. Both rating1 and rating2 are dictionaries

       of the form {'The Strokes': 3.0, 'Slightly Stoopid': 2.5}"""

    distance = 0

    commonRatings = False 

    for key in rating1:

        if key in rating2:

            distance += pow(abs(rating1[key] - rating2[key]),r)

            commonRatings = True

    if commonRatings:

        return pow(distance, 1.0/r)

    else:

        return -1 #Indicates no ratings in common

def cosineSimilarity (rating1, rating2):

    """Computes the Cosine Similarity distance. Both rating1 and rating2 are dictionaries

       of the form {'The Strokes': 3.0, 'Slightly Stoopid': 2.5}"""

    sum_xy = 0

    sum_sqr_x = 0

    sum_sqr_y = 0

    for key in teams:

        if key in rating1 and key in rating2:

            sum_xy += rating1[key]* rating2[key]

            sum_sqr_x += pow(rating1[key], 2)

            sum_sqr_y += pow(rating2[key], 2)

        elif key not in rating1 and key in rating2:

            sum_xy += 0

            sum_sqr_x += 0

            sum_sqr_y += pow(rating2[key], 2)

        elif key in rating1 and key not in rating2:

            sum_xy += 0

            sum_sqr_x += pow(rating1[key], 2)

            sum_sqr_y += 0

        else:

            sum_xy += 0

            sum_sqr_x += 0

            sum_sqr_y += 0

    if sum_sqr_x ==0 or sum_sqr_y==0:

        return -1 #Indicates no ratings in common

    else:

        return sum_xy / (sqrt(sum_sqr_x) * sqrt(sum_sqr_y))

def pearson(rating1, rating2):

    """Computes the pearson distance. Both rating1 and rating2 are dictionaries

       of the form {'The Strokes': 3.0, 'Slightly Stoopid': 2.5}"""

    sum_xy = 0

    sum_x = 0

    sum_y = 0

    sum_x2 = 0

    sum_y2 = 0

    n = 0

    for key in rating1:

        if key in rating2:

            n += 1

            x = rating1[key]

            y = rating2[key]

            sum_xy += x * y

            sum_x += x

            sum_y += y

            sum_x2 += pow(x, 2)

            sum_y2 += pow(y, 2)

    # now compute denominator

    denominator = sqrt(sum_x2 - pow(sum_x, 2) / n) * sqrt(sum_y2 - pow(sum_y, 2) / n)

    if denominator == 0:

        return 0

    else:

        return (sum_xy - (sum_x * sum_y) / n) / denominator